Распределенные силы

В инженерных расчетах часто приходится встречаться с нагрузками, распределенными вдоль данной поверхности. Рассмотрим некоторые примеры распределенных сил, лежащих в одной плоскости.

Плоская система распределенных сил характеризуется ее интенсивностью , т. е. значением силы, приходящейся на единицу длины нагруженного отрезка. Измеряется интенсивность в ньютонах, деленных на метры (Н/м).

1 ) Силы, равномерно распределенные вдоль отрезка прямой (рис. 69, а). Для такой системы сил интенсивность имеет постоянное значение. При статических расчетах эту систему сил можно заменить равнодействующей .

По модулю,

. (35)

Приложена сила в середине отрезка .

2) Силы, распределенные вдоль отрезка прямой по линейному закону (рис. 69, б). Примером такой нагрузки могут служить силы давления воды на плотину, имеющие наибольшее значение у дна и падающие до нуля у поверхности воды. Для этих сил интенсивность является величиной переменной, растущей от нуля до максимального значения . Равнодействующая таких сил определяется аналогично равнодействующей сил тяжести, действующих на однородную треугольную пластину . Так как вес однородной пластины пропорционален ее площади, то, по модулю,

. (36)

Приложена сила на расстоянии от стороны треугольника (см. § 35, п. 2).

3) Силы, распределенные вдоль отрезка прямой по произвольному закону (рис. 69, б). Равнодействующая таких сил, по аналогии с силой тяжести, по модулю равна площади фигуры , измеренной в соответствующем масштабе, и проходит через центр тяжести этой площади (вопрос об определении центров тяжести площадей будет рассмотрен в § 33).

Расчет плоских ферм

Пример решения задач на равновесие системы тел дает расчет ферм. Фермой называется жесткая конструкция из прямолинейных стержней, соединенных на концах шарнирами. Если все стержни фермы лежат в одной плоскости, ферму называют плоской. Места соединения стержней фермы называют узлами. Все внешние нагрузки к ферме прикладываются только в узлах. При расчете фермы трением в узлах и весом стержней (по сравнению с внешними нагрузками) пренебрегают или распределяют веса стержней по узлам. Тогда на каждый из стержней фермы будут действовать две силы, приложенные к его концам, которые при равновесии могут быть направлены только вдоль стержня. Следовательно, можно считать, что стержни фермы работают только на растяжение или на сжатие. Ограничимся рассмотрением жестких плоских ферм без лишних стержней, образованных из треугольников. В таких фермах число стержней и число узлов связаны соотношением

. (38)

Расчет фермы сводится к определению опорных реакций и усилий в ее стержнях.

Опорные реакции можно найти обычными методами статики (см. § 17), рассматривая ферму в целом как твердое тело. Перейдем к определению усилий в стержнях.

Метод вырезания узлов. Этим методом удобно пользоваться, когда надо найти усилия во всех стержнях фермы. Он сводится к последовательному рассмотрению условий равновесия сил, сходящихся в каждом из узлов.

Если в ходе расчета встретится узел, для которого число неизвестных больше двух, то можно воспользоваться методом сечений.

Метод сечений (метод Риттера). Этим методом удобно пользоваться для определения усилий в отдельных стержнях фермы, в частности для проверочных расчетов. Идея метода состоит в том, что ферму разделяют на две части сечением, проходящим через три стержня, в которых (или в одном из которых) требуется определить усилия, и рассматривают равновесие одной из этих частей. Действие отброшенной части заменяют соответствующими силами, направляя их вдоль разрезанных стержней от узлов, т. е. считая стержни растянутыми (как и в методе вырезания узлов). Затем со­ставляют уравнения равновесия в форме (31) или (30), беря центры моментов (или ось проекций) так, чтобы в каждое уравнение вошло только одно неизвестное усилие.

ЗАКОНЫ ТРЕНИЯ СКОЛЬЖЕНИЯ

Опыт показывает, что при стремлении двигать одно тело по по­верхности другого в плоскости соприкосновения тел возникает сила сопротивления их относительному скольжению, называемая силой трения скольжения.

Возникновение трения обусловлено прежде всего шероховато­стью поверхностей, создающей сопротивление перемещению, и на­личием сцепления у прижатых друг к другу тел. Изучение всех особенностей явления трения представляет собой довольно слож­ную физико-механическую проблему, рассмотрение которой выхо­дит за рамки курса теоретической механики.

В инженерных расчетах обычно исходят из ряда установленных опытным путем закономерностей, которые с достаточной для прак­тики точностью отражают основные особенности явления трения. Эти закономерности, называемые законами трения скольжения при покое, можно сформулировать Следующим образом.

1. При стремлении сдвинуть одно тело по поверхности другого в плоскости соприкосновения тел возникает сила трения (или сила сцепления), которая может принимать любые значения от нуля до значения называемого предельной силой трения.

Приложенная к телу сила трения направлена в сторону, про­тивоположную той, куда действующие на тело силы стремятся его сдвинуть.

2. Предельная сила трения численно равна произведению стати­ческого коэффициента трения на нормальное давление или нормаль­ную реакцию:

. (39)

Статический коэффициент трения — величина безразмерная; он определяется опытным путем и зависит от материала соприкасаю­щихся тел и состояния поверхностей (характер обработки, темпера­тура, влажность и т.п.).

3. Значение предельной силы трения в довольно широких пре­делах не зависит от размеров соприкасающихся при трении по­верхностей.

Из первых двух законов следует, что при равновесии или

. (40)

Следует подчеркнуть, что значение силы трения при покое опре­деляется неравенством (40) и что, следовательно, это значение мо­жет быть любым, но не большим, чем . Чему конкретно равна сила трения, можно установить, только решив соответствующую задачу (см. § 25). Величине сила трения будет равна лишь тогда, когда действующая на тело сдвигающая сила достигает такого зна­чения, что при малейшем ее увеличении тело начинает двигаться (скользить). Равновесие, имеющее место, когда сила трения равна , будем называть предельным равновесием.

В заключение приведем значения коэффициента трения для некоторых материалов: дерево по дереву 0,4—0,7; металл по металлу 0,15—0,25; сталь по льду 0,027.

Более подробные сведения даются в соответствующих справочни­ках.

Все изложенное выше относилось к трению скольжения при покое. При движении сила трения направлена в сторону, противо­положную движению, и равна произведению динамического коэф­фициента трения на нормальное давление *:

.

Динамический коэффициент трения скольжения также являет­ся величиной безразмерной и определяется опытным путем. Значе­ние коэффициента зависит не только от материала и состояния поверхностей, но и в некоторой степени от скорости/движущихся тел. В большинстве случаев с увеличением скорости коэффициент сначала несколько убывает, а затем сохраняет почти постоянное значение.

РЕАКЦИИ ШЕРОХОВАТЫХ СВЯЗЕЙ. УГОЛ ТРЕНИЯ

Р еакция реальной (шероховатой) связи слагается из двух состав­ляющих: из нормальной реакции и перпендикулярной ей силы трения . Следовательно, полная реакция будет отклонена от нормали к поверхности на некоторый угол. При изменении силы трения от нуля до у сила . изменяется от до , а ее угол с нормалью растет от нуля до некоторого предельного значения (рис. 75). Наибольший угол , который полная реакция шерохова­той связи образует с нормалью к поверхности, называется углом трения. Из чертежа видно, что

.

Так как , то отсюда находим следующую связь между углом трения и коэффициентом трения:

.

При равновесии полная реакция в зависимости от сдвигающих сил может проходить где угодно внутри угла трения. Когда равно­весие становится предельным, реакция будет отклонена от нормали на угол .

Если к телу, лежащему на шероховатой поверхности, приложить

силу , образующую угол с нормалью (рис. 76), то тело сдвинется только тогда, когда сдвигающее усилие будет больше (мы считаем , пренебрегая весом тела). Но неравенство , в котором , выполняется только при , т.е. при . Следовательно, никакой силой, образующей с нормалью угол , меньший угла трения , тело вдоль данной поверхности сдвинуть нельзя. Этим объясняются известные явления заклинивания или самоторможения тел.

Изучение равновесия тел с учетом трения скольжения можно свести к рассмотрению предельного равновесия, которое имеет мес­то, когда сила трения равна .

При аналитическом решении реакцию шероховатой связи изобра­жают двумя ее составляющими . Затем составляют обычные уравнения равновесия и присоединяют к ним равенство . Из полученной таким путем системы уравнений и определяют искомые величины.

Если в задаче требуется определить условия равновесия при всех значениях, которые может иметь сила трения, т.е. при , то ее тоже можно решить, рассмотрев предельное равновесие и уменьшая затем в полученном результате коэффициент трения до нуля *.

В самом деле, когда равновесие является предельным, сила трения . В остальных положениях равновесия . Следовательно, в каждом из этих положений можно считать , где . При (или ) получим положение равновесия, соответствующие случаю, когда связь является гладкой (идеальной).

При геометрическом решении реакцию шероховатой связи удоб­нее изображать одной силой , которая в предельном положении равновесия отклонена от нормали к поверхности на угол .

ТРЕНИЕ КАЧЕНИЯ

Трением качения называется сопротивление, возникающее при качении одного тела по поверхности другого.

Р ассмотрим круглый цилиндрический каток радиуса и веса , лежащий на горизонтальной шероховатой плоскости. Приложим к оси катка силу (рис. 83, а), меньшую . Тогда в точке воз­никает сила трения , численно равная , которая будет препятст­вовать скольжению цилиндра по плоскости. Если считать нормаль­ную реакцию тоже приложенной в точке , то она уравновесит силу , а силы и образуют па­ру, вызывающую качение цилинд­ра. При такой схеме качение долж­но начаться, как видим, под дей­ствием любой, сколь угодно малой силы .

Истинная же картина, как по­казывает опыт, выглядит иначе.

Объясняется это тем, что фактически вследствие деформаций тел касание их происходит вдоль некоторой площадки (рис. 83, б). При действии силы интенсивность давления у края убывает, а у края возрастает. В результате реакция оказывается сме­щенной в сторону действия силы . С увеличением это смещение растет до некоторой предельной величины . Таким образом, в предельном положении на каток будут действовать пара с моментом и уравновешивающая ее пара , с моментом . Из равенства моментов находим или

. (43)

Пока каток находится в покое; при начинается качение.

Входящая в формулу (43) линейная величина называется коэффициентом трения качения. Измеряют величину обычно в сантиметрах. Значение коэффициента зависит от материала тел и определяется опытным путем. Приведем приближенные значения этого коэффициента (в см) для некоторых материалов:

Дерево по дереву ...........

Сталь мягкая по стали (колесо по рельсу)

Сталь закаленная по стали (шариковый подшипник) .............

Отношение для большинства материалов значительно мень­ше статического коэффициента трения . Этим объясняется то, что в технике, когда это возможно, стремятся заменить скольжение качением (колеса,, катки, шариковые подшипники и т. п.).

ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ

МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ.

ВЫЧИСЛЕНИЕ ГЛАВНОГО ВЕКТОРА И ГЛАВНОГО МОМЕНТА СИСТЕМЫ СИЛ

В § 8 было введено понятие о моменте силы относительно центра О. Это вектор , направленный перпендикулярно плос­кости ОАВ (рис. 85), модуль которого согласно формуле (13) имеет значение

=2 пл. ОАВ.

Как это было и для силы, в дальнейшем окажется необходимым рассматривать проекции вектора на разные оси. Проекция вектора , т. е. момента си­лы относительно центра О, на какую-нибудь ось z, проходящую через этот центр, называется мо­ментом силы относительно оси z, т. е.

или ,(44)

где — момент силы относительно оси z; — угол между век­тором и осью z. Из определения следует, что , как про­екция вектора на ось, является величиной алгебраической (знак определяется так же, как знак проекции любого вектора; например. на рис. 85 >0).

Найдем другое выражение для , позволяющее непосредст­венно вычислять эту величину. Для этого проведем через произ­вольную точку O₁ оси z (рис. 85) плоскость ху, перпендикулярную этой оси, и спроектируем ОAВ на эту плоскость. Так как вектор перпендикулярен плоскости ОАВ, а ось г перпендикулярна плоскости O₁A₁B₁, то угол у, как угол между нормалями к назван­ным плоскостям, является углом между этими плоскостями. Следо­вательно, если одновременно учесть равенство (44), то

2пл. O₁A₁B₁= 2 пл. ОAВ = .

Но, как видно из рис. 85, в треугольнике сторона A₁B₁ представляет собой одновременно проекцию силы на плоскость ху (см. §5). Тогда 2пл. О₁A₁B₁=F_xyh= , где - алгебраический момент силы относительно центра О₁. Из этого и предыдущего равенств следует (с учетом знаков), что

или .(45)

Таким образом, момент силы относительно оси z равен алгеб­раическому моменту проекции этой силы на плоскость, перпенди­кулярную оси z, взятому относительно точки О₁ пересечения оси с этой плоскостью. Этот результат может служить другим определе­нием понятия момента силы относительно оси.

Замечая как направлен поворот, который стремится совершить сила , когда >0 (см. рис. 85; случай, когда <0 получится, если изменить направление силы на прямо противо­положное), приходим к следующему выводу: момент силы относи­тельно оси будет иметь знак плюс, когда с положительного конца оси поворот, который стремится совершить сила , виден проис­ходящим против хода часовой стрелки, и знак минус — когда по ходу часовой стрелки.

Из рис. 85 видно еще, что если менять положение точки O на оси z, то и модуль и направление вектора будут при этом из­меняться, но O₁A₁B₁, а с ним и значение изменяться не будут.

Механический смысл величины состоит в том, что она ха­рактеризует вращательный эффект силы , когда эта сила стремится повернуть тело вокруг оси z. В самом деле, если разложить силу на составляющие и , где \\O_z (рис. 86), то поворот вокруг оси z будет совершать только составляющая и вращательный эффект всей силы будет, согласно формуле (45), определяться ве­личиной . Составляющая же повернуть тело вокруг оси z не может (она лишь может сдвинуть тело вдоль оси z).

В заключение рассмотрим подробнее, как вычисляется момент силы относительно оси z по формуле (45). Для этого надо (рис. 87):

1) провести плоскость ху, перпендикулярную оси z (в любом месте);

2) спроектировать силу на эту плоскость и найти величину ;

3) опустить из точки пересечения оси с плоскостью (на рис. 87 это точка О) перпендикуляр на линию действия и найти его длину h;

4) вычислить произведение ; 5) определить знак момента.

При вычислении моментов надо иметь в виду следующие частные случаи:

1) если сила параллельна оси, то ее момент относительно оси ра­вен нулю (так как =0);

2) если линия действия силы пересекает ось, то ее момент отно­сительно оси также равен нулю (так как h=0).

Объединяя оба случая вместе, заключаем, что момент силы отно­сительно оси равен нулю, если сила и ось лежат в одной плоскости;

3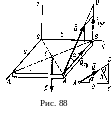 ) если сила перпендикулярна оси (лежит в плоскости, перпен­дикулярной этой оси), то ее момент относительно оси равен взятому с соответствующим знаком произ­ведению модуля силы на расстоя­ние между линией действия силы и осью, т. е. вычисляется по форму­ле (45), в которую вместо вой­дет модуль силы F.

ЦЕНТР ТЯЖЕСТИ

СИЛОВОЕ ПОЛЕ.

ЦЕНТР ТЯЖЕСТИ ТВЕРДОГО ТЕЛА

Область, в каждой точке которой на помещенную туда материальную частицу действует сила, зависящая от положения (координат) этой точки, называется силовым полем¹. Примером силового поля является поле тяготения (поле сил притяжения к Земле или к любому другому небесному телу).

На каждую частицу тела, находящегося вблизи земной поверхности, действует направленная вертикально вниз сила, которую называют силой тяжести (вопрос о том, что собой представляет сила тяжести, будет рассмотрен в § 92). Эти силы образуют поле сил тяжести.

Для тел, размеры которых очень малы по сравнению с земным радиусом, силы тяжести, действующие на частицы тела, можно считать параллельными друг другу и сохраняющими для каждой частицы постоянное значение при любых поворотах тела. Поле тяжести, в котором выполняются эти два условия, называют однородным полем тяжести.

Р авнодействующую сил тяжести , действующих на частицы данного тела, обозначим (рис. 105). Модуль этой силы называется весом тела и определяется равенством

. (58)

При любом повороте тела силы остаются приложенными в одних и тех же точках тела и параллельными друг другу, изменяется только их направление по отношению к телу. Следовательно, по доказанному в § 31, равнодействующая сил будет при любых положениях тела проходить через одну и ту же неизменно связанную с телом точку С, являющуюся центром параллельных сил тяжести . Эта точка и называется центром тяжести тела. Таким образом, центром тяжести твердого тела называется неизменно связанная с этим телом точка, через которую проходит линия действия равнодействующей сил тяжести, действующих на частицы данного тела, при любом положении тела в пространстве.

Координаты центра тяжести, как центра параллельных сил, определяются формулами (57); следовательно,

, (59)

где — координаты точек приложения сил тяжести , действующих на частицы тела.

Отметим в заключение, что согласно определению центр тяжести — это точка геометрическая; она может лежать и вне пределов данного тела (например, для кольца).

КООРДИНАТЫ ЦЕНТРОВ ТЯЖЕСТИ ОДНОРОДНЫХ ТЕЛ

Для однородного тела вес p_k любой его части пропорционален объему , этой части: , а вес Р всего тела пропорционален объему V этого тела, т. е. , где — вес единицы объема.

Подставив эти значения Р и р_k в формулы (59), заметим, что во всех суммах у как общий множитель выносится за скобки и сокращается с в знаменателе. В результате из формул (59) получим:

. (60)

Как видно, положение центра тяжести однородного тела зависит только от его геометрической формы, а от величины не зависит. По этой причине точку С, координаты которой определяются формулами (60), называют центром тяжести объема V.

Путем аналогичных рассуждении легко найти, что если тело представляет собой однородную плоскую и тонкую пластину, то для нее

, (61)

где S — площадь всей пластины; s_k — площади ее частей.

Точку, координаты которой определяются формулами (61), называют центром тяжести площади S.

Точно так же получаются формулы для координат центра тяжести линии:

,(62)

где L — длина всей линии; l_k — длины ее частей.

По формулам (62) можно находить центры тяжести изделий из тонкой проволоки постоянного сечения.

Таким образом, центр тяжести однородного тела определяется, как центр тяжести соответствующего объема, площади или линии.

СПОСОБЫ ОПРЕДЕЛЕНИЯ КООРДИНАТ ЦЕНТРОВ ТЯЖЕСТИ ТЕЛ

Исходя из полученных выше общих формул, можно указать конкретные способы определения координат центров тяжести тел.

1.Симметрия. Если однородное тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно или в плоскости симметрии, или на оси симметрии, или в центре симметрии.

Допустим, например, что однородное тело имеет плоскость симметрии. Тогда этой плоскостью оно разбивается на две такие части, веса которых и равны друг другу, а центры тяжести находятся на одинаковых расстояниях от плоскости симметрии. Следовательно, центр тяжести тела как точка, через которую проходит равнодействующая двух равных и параллельных сил и , будет действительно лежать в плоскости симметрии. Аналогичный результат получается и в случаях, когда тело имеет ось или центр симметрии.

Из свойств симметрии следует, что центр тяжести, однородного круглого кольца, круглой или прямоугольной пластины, прямоугольного параллелепипеда, шара и других однородных тел, имеющих центр симметрии, лежит в геометрическом центре (центре симметрии) этих тел.

2. Разбиение. Если тело можно разбить на конечное число таких частей, для каждой из которых положение центра тяжести известно, то координаты центра тяжести всего тела можно непосредственно вычислить по формулам (59) — (62). При этом число слагаемых в каждой из сумм будет .равно числу частей, на которые разбито тело.

3. Дополнение. Этот способ является частным случаем способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны.

4. Интегрирование. Если тело нельзя разбить на несколько конечных частей, положения центров тяжести которых известны, то тело разбивают сначала на произвольные малые объемы , для которых формулы (60) принимают вид

и т.д (63)

где x_k,y_k,z_k — координаты некоторой точки, лежащей внутри объема . Затем в равенствах (63) переходят к пределу, устремляя все к нулю, т.е. стягивая эти объемы в точки. Тогда стоящие в равенствах суммы обращаются в интегралы, распространенные на весь объем тела, и формулы (63) дают в пределе:

, (64)

Аналогично для координат центров тяжести площадей и линий получаем в пределе из формул (61) и (62):

И

(66)

Пример применения этих формул к определению координат центра тяжести рассмотрен в следующем параграфе.

5 . Экспериментальный способ. Центры тяжести неоднородных тел сложной конфигурации (самолет, паровоз и т.п.) можно определять экспериментально. Один из возможных экспериментальных методов (метод подвешивания) состоит в том, что тело подвешивают на нити или тросе за различные его точки. Направление нити, на которой подвешено тело, будет каждый раз давать направление силы тяжести. Точка пересечения этих направлений определяет центр тяжести тела. Другим возможным способом экспериментального определения центра тяжести является метод взвешивания. Идея этого метода ясна из рассмотренного ниже примера.

ЦЕНТРЫ ТЯЖЕСТИ НЕКОТОРЫХ ОДНОРОДНЫХ ТЕЛ.

Центр тяжести дуги окружности. Рассмотрим дугу радиуса R с центральным углом АОВ=2 . В силу симметрии центр тяжести этой дуги лежит на оси Ох (рис. 109). Найдем координату x_c по формулам (66). Для этого выделим на дуга АВ элемент ММ' длиной dl=Rdφ, положение которого определяется углом φ. Координата х элемента ММ' будет x=Rcosα . Подставляя эти значения х и dl в первую из формул (66) и имея в виду, что интеграл должен быть распространен на всю длину дуги, получим:

,

где L — длина дуги АВ, равная R^.2 . Отсюда окончательно находим, что центр тяжести дуги окружности лежит на ее оси симметрии на расстоянии от центра О, равном

, (67)

где угол , измеряется в радианах.

. Центр тяжести площади треугольника. Разобьем площадь треугольника АВО (рис. 110) прямыми, параллельными стороне АВ, на п узких полосок; центры тяжести этих полосок будут лежать на медиане ВЕ треугольника. Следовательно, и центр тяжести всего треугольника лежит на этой медиане. Аналогичный результат получается для двух других медиан. Отсюда заключаем, что центр тяжести площади треугольника лежит в точке пересечения его медиан. При этом, как известно,

. (68)

3 .Центр тяжести площади кругового сектора. Рассмотрим круговой сектор ОАВ радиуса R с центральным углом (рис. 111). Разобьем мысленно площадь сектора ОАВ радиусами, проведенными из центра О, на п секторов. В пределе при неограниченном увеличении числа п, эти секторы можно рассматривать как плоские треугольники, центры тяжести которых лежат на дуге DЕ радиуса 2R/3. Следовательно, центр тяжести сектора ОАВ совпадает с центром тяжести дуги ВЕ, положение которого найдется по формуле (67). Окончательно получим, что центр тяжести площади кругового сектора лежит на его оси симметрии на расстоянии от центра О, равном

. (69)

Приведем без доказательств еще два результата.

4. Центр тяжести объема пирамиды (или конуса). Этот центр С лежит на прямой С₁Е (рис. 112), где Е — вершина, а С₁ — центр тяжести площади основания пирамиды, при этом

. (70)

Результат справедлив для любой многоугольной пирамиды и для конуса.

5. Центр тяжести объема полушара. Этот центр С лежит на оси Ох (оси симметрии, рис. 113), а его координата

, (71)

где R — радиус полушара.

Формулы, определяющие координаты центров тяжести других однородных тел, можно найти в различных технических справочниках.