
- •Часть IV
- •Санкт-Петербург
- •1.1. Основные понятия
- •1.2. Действия с матрицами
- •2. Определители
- •3. Обращение квадратных матриц
- •4. Ранг матрицы
- •4.1. Элементарные преобразования не изменяют ранга матрицы.
- •4.3. Любой ряд матрицы можно представить в виде линейной комбинации параллельных базисных рядов.
- •4.4. Для того чтобы определитель квадратной матрицы был равен нулю, необходимо и достаточно,
- •5. Системы линейных уравнений
- •5.3.7. Если (система имеет бесчисленное множество решений), то каждому набору
- •5.4.1. Теорема Крамера
- •5.4.2. Если система 5.4. - однородна, то она имеет ненулевое решение в том и только в том случае,
- •5.5. Метод обратной матрицы
- •6. Векторное n-мерное пространство
- •7. Собственные числа и собственные векторы
- •Выпуклые множества
- •- Выпуклое множество.
- •- Выпуклое множество.
- •9. Производная по направлению, градиент
- •9.1. Градиентом данной функции в данной будем называть вектор, координатами
- •9.3. Наискорейшее возрастание функции происходит при движении от данной точки в направлении градиента.
- •9.4. Градиент функции в данной перпендикулярен к касательной линии уровня в этой точке.
- •10. Векторы и системы линейных уравнений в экономике
- •10.1. Модель Леонтьева (основная задача межотраслевого баланса)
- •10.2. Линейная модель обмена (модель международной торговли)
- •11. Метод полного исключения для решения системы линейных уравнений
- •3. Третий шаг решения (III шаг) состоит в том, что неизвестная исключается из всех уравнений кроме третьего, а в третье должна входить с коэффициентом единица.
- •Литература
- Выпуклое множество.
Примеры выпуклых множеств:
прямая в
![]() ,
плоскость в
,
плоскость в
![]() ,
гиперплоскость в
,
пространство
,
полупространство в
,
пересечение полупространств.
,
гиперплоскость в
,
пространство
,
полупространство в
,
пересечение полупространств.
Определение Выпуклое множество будем называть ограниченным, если ограничены все координаты всех его точек.

 Примеры Гиперплоскость,
полупространство и пространство –
неограниченные множества.
Примеры Гиперплоскость,
полупространство и пространство –
неограниченные множества.

P
O S

![]() - ограниченное множество.
- ограниченное множество.
9. Производная по направлению, градиент
Рассмотрим функцию
![]() ,
которая определена, непрерывна и
дифференцируема в заданной области D.
,
которая определена, непрерывна и
дифференцируема в заданной области D.
Внутри области выберем произвольную
![]() области D.
области D.
9.1. Градиентом данной функции в данной будем называть вектор, координатами
которого являются частные производные этой функции, вычисленные в этой точке.
![]() .
.
Зададим вектор
![]() следующим образом:
следующим образом:
![]() .
.
Выберем в области D
произвольную
![]() так, чтобы выполнялось условие:
так, чтобы выполнялось условие:
![]() .
.
Если
![]() - переменные, то точка М будет
перемещаться по области в данном
направлении
.
- переменные, то точка М будет
перемещаться по области в данном
направлении
.


![]() М
М
![]()
![]() М0
М0

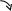

![]()
 О
О
![]()
![]()
![]()
Из заданных условий следует:
![]() .
.
Полное приращение функции
![]() ,
где
,
где
![]() - бесконечно малые более высокого
порядка малости, чем
- бесконечно малые более высокого
порядка малости, чем
![]() .
.
Пусть
![]() .
.
Скорость изменения функции при движении точки от в данном направлении измеряется с помощью специальной производной, которую называют “производная по направлению”.
9.2. Производной по направлению
данной функции
в данном направлении
,
вычисленной в данной точке
будем назывть предел отношения
полного приращения функции
![]() к вызвавшему его приращению
вектора-направления
к вызвавшему его приращению
вектора-направления
![]() , при условии, что последнее стремится
к нулю, а также при условии, что такой
предел существует и конечен.
, при условии, что последнее стремится
к нулю, а также при условии, что такой
предел существует и конечен.
![]() .
.
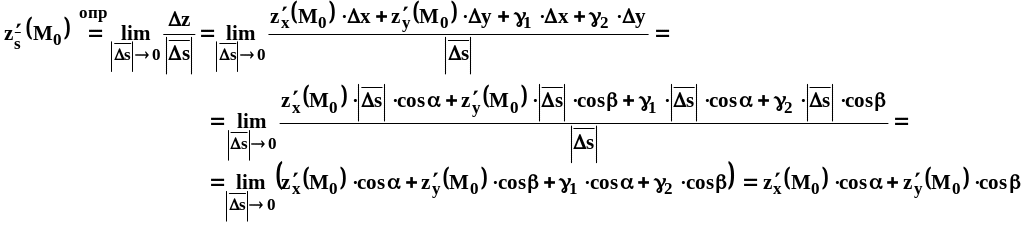
![]() .
.
9.3. Наискорейшее возрастание функции происходит при движении от данной точки в направлении градиента.
![]() ,
поэтому принимает максимальное значение,
когда
,
поэтому принимает максимальное значение,
когда
![]() .
.
