5. Характеристичний та мінімальний многочлени матриці

Нехай – квадратна матриця порядку над полем .

Означення. Характеристичною матрицею матриці називається матриця

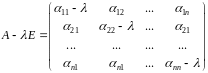
із змінною , яка набуває будь-які числові значення.

Означення. Характеристичним многочленом матриці називається визначник характеристичної матриці:

,

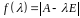який являє собою многочлен від змінної степеня . Корені характеристичного многочлена називаються характеристичними коренями або характеристичними числами матриці .

В довільний многочлен 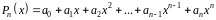замість змінної можна підставити квадратну матрицю порядку .

Означення. Якщо для заданої квадратної матриці порядку 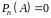, то називається матричним коренем многочлена 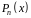, а многочлен називається многочленом, що анулюється матрицею .

Має місце теорема.

Теорема (Гамільтона-Келі). Кожна матриця є коренем свого характеристичного многочлена.

Означення. Мінімальним многочленом матриці над полем називається нормований многочлен 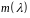найменшого степеня, що анулюється матрицею .

Теорема (про анулюючий многочлен). Будь-який многочлен, що анулюється матрицею , ділиться без остачі на мінімальний многочлен матриці . Зокрема, характеристичний многочлен матриці ділиться без остачі на мінімальний многочлен матриці .

Наслідок. Будь-який корінь мінімального многочлена матриці є її характеристичним коренем.

Коренями мінімального многочлена є всі різні корені характеристичного многочлена 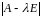причому, якщо

,

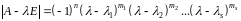то

,

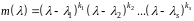де , .

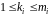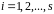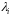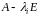Для побудови мінімального многочлена матриці для кожного характеристичного кореня , , складають матрицю і підносять її до степенів 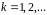доти, поки не буде виконана рівність :

,

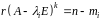де 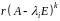– ранг матриці 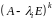; – порядок матриці ; 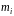– кратність характеристичного кореня матриці . Найменше натуральне число , при якому виконується рівність , дає кратність 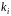кореня в мінімальному многочлені матриці .

Також для побудови мінімального многочлена матриці можна застосовувати теорему про анулюючий многочлен.

Приклад. Знайти мінімальний многочлен матриці

.

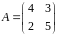Розв’язання. Характеристичний многочлен матриці

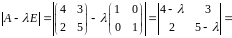
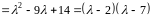
має два простих кореня 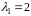і 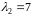. При цьому

,

,

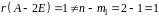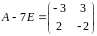
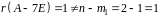Таким чином, і є коренями мінімального многочлена. Отже, мінімальний многочлен є .

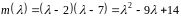Другий спосіб. За теоремою про анулюючий многочлен мінімальним многочленом може бути один з многочленів 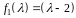, , 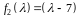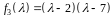. Треба перевірити, які з цих многочленів є анулюючими і вибрати з них многочлен мінімального степеня.

;

;

.

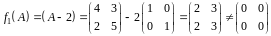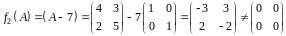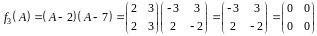Отже, мінімальний многочлен є .

6. Мінімальний многочлен вектора відносно матриці

Нехай – квадратна матриця порядку над полем , .

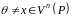Означення. Мінімальним многочленом вектора відносно матриці називається нормований многочлен 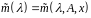найменшого степеня, для якого .

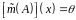Коли матриця є відомою з контексту, цей многочлен часто називають мінімальним многочленом вектора , або просто відносним мінімальним многочленом.

Оскільки 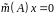для довільного вектора 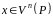, то 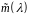іноді називають мінімальним многочленом всього простору 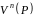відносно матриці .

Відносний мінімальний многочлен визначається однозначно. Якщо 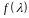довільний многочлен, який анулює вектор , тобто 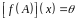, то ділиться на .

Для побудови мінімального многочлена вектора відносно матриці розглянемо послідовність векторів 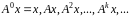. На кожному кроці будемо перевіряти, чи є система отриманих векторів лінійно незалежною. В силу скінченновимірності простору знайдеться таке ціле число , 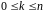, що вектори 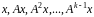будуть лінійно незалежні, а вектор 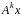буде лінійною комбінацією цих векторів з коефіцієнтами з поля . Інакше кажучи, знайдуться коефіцієнти, не всі рівні нулю, що виконається співвідношення . 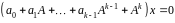Цьому співвідношенню відповідає многочлен

,

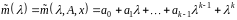який залежить від матриці та вектора .

Справедливі наступні властивості мінімального многочлена вектора :

1. Мінімальний многочлен суми векторів є найменшим спільним кратним мінімальних многочленів векторів-доданків.

2. Мінімальний многочлен суми лінійно незалежних векторів є добутком їхніх мінімальних многочленів

3. Мінімальний многочлен матриці ділиться на мінімальний многочлен довільного вектора .

Очевидно, найменше спільне кратне мінімальних многочленів базисних векторів відносно матриці є мінімальним многочленом цієї матриці.