4. Визначник матриці

4.1 Підстановки

Нехай – скінченна множина з елементів.

Підстановкою порядку на множині з елементів називається взаємно однозначне відображення множини на себе.

Нехай впорядкована, тоді їй відповідає послідовність номерів 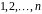. Після застосування підстановки порядок елементів зміниться і прийме вигляд .

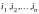Підстановку можна представити у вигляді дворядного запису: .

Очевидно, обернене перетворення має вигляд .

Підстановки утворюють групу відносно операції композиції, яка позначається 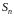Порядок групи підстановок дорівнює .

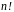Композицією (добутком) підстановок і називається результат їхньої послідовної дії. Таким чином, якщ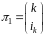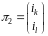о, , , то 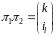. Очевидно, існує обернений елемент 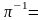, а також, одиничний елемент – тотожна підстановка 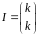, для якої 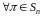і, таким чином, дійсно є групою.

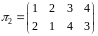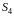
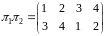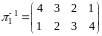Приклад. Для , з , , а .

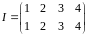4.2 Підстановочні матриці

Підстановку 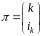можна задати (представити) як матрицю. Існує ізоморфне відображення . Матриця вигляду 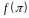, , 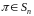називається матрицею підстановки, або підстановочною матрицею.

В підстановочній матриці 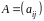порядку елементи з індексами 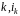дорівнюють одиниці, а інші елементи дорівнюють нулю. Наприклад, для підстановки 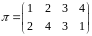отримаємо .

Оскільки , то матриця реалізує підстановку .

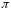Виходячи з означення підстановки, підстановочні матриці оборотні. Якщо матриця 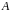підстановочна, т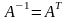о , тому, що .

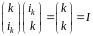4.3 Цикли, транспозиції

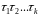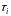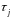Кожну підстановку можна представити у вигляді добутку деяких спеціальних підстановок, як називаються циклами, причому цикли попарно незалежні. Останнє означає, що підстановки і , при , діють на підмножинах підстановки, що не перерізаються, якщо не брати до уваги елементи, що залишаються нерухомими.

Нехай 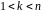и – підстановка степеня , причому .

Означення. Підстановка називається -членним циклом, якщо вона не переміщає елементів, а її дію на ті елементи, що залишилися, 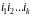можна представити у вигляді циклічної діаграми переходів: . У цій діаграмі допускається лише один перехід від елементу з більшим індексом до елементу з меншим індексом, а саме: .

Наприклад, в тричленному циклі п'ятого степеня . елементи 4 і 5 нерухомі, а елементи 1,2,3 утворюють цикл, причому , , .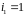

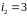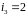Циклічна діаграма переходів може бути виписана, починаючи з будь-якого свого елементу. Цикл записують у вигляді, аналогічному діаграмі переходів: 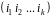. Нерухомим елементам зіставляються так звані одиничні цикли виду . Одиничну підстановку розглядають як добуток одночленних циклів вигляду .

Для запису підстановки у вигляді добутку незалежних циклів достатньо виписати всі різні діаграми переходів. Наприклад, підстановка може бути представлена як 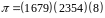. Тут число циклів дорівнює 3. Як правило, одночленні цикли в записі часто опускаються.

Запис підстановки у вигляді добутку незалежних циклів називається цикловим записом. Оскільки цикли незалежні, то порядок циклів у цикловому записі підстановки є довільним.

Означення. Цикловою структурою підстановки 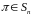називається запис виду 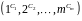, який означає, що розкладається в добуток 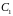циклів довжини 1, циклів довжини 2, і так далі, 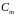циклів довжини .

Підстановка називається регулярною, якщо її циклічний запис складається з циклів рівної довжини.

Підстановка називається повноцикловою, якщо її цикловий запис складається з одного циклу.

Найбільш простим циклом, очевидно, є підстановка, яка переставляє місцями лише два елементи.

Означення. Цикл довжини 2 називається транспозицією.

Транспозиції не обов'язково є незалежними циклами.

Нехай – підстановка з , – будь-який її розклад в добуток транспозицій. Тоді число , яке називається знаком (або сигнатурою, або парністю ) повністю визначається підстановкою і не залежить від способу розкладу в добуток транспозицій.