2. Лінійні оператори і матриці

Нехай у векторному просторі заданий деякий базис .

Означення. Матрицею лінійного оператора в базисі називається матриця

,

елементами якої є коефіцієнти в розкладі образів векторів за базисом , тобто

;

;

………………………………………..

.

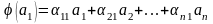З означення випливає, що стовпцями матриці є координатні рядки векторів , , в базисі .

При фіксованому базисі кожному лінійному оператору простору відповідає певна матриця -го порядку – матриця цього лінійного оператора . Справедливе і обернене: кожна матриця -го порядку є матрицею певного лінійного оператора простору в базисі .

У координатному вигляді дія лінійного оператора на вектор зводиться до множення матриці лінійного оператора на координатний стовпчик вектора :

.

Ясно, що матриця оператора залежить від вибору базису простору .

Знайдемо матриці деяких лінійних операторів з попередніх прикладів:

Приклади.

1) Матрицею нульового оператора є нульова матриця .

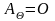2) Матрицею тотожного оператора є одинична матриця: , Тотожний оператор будь-який вектор переводить в вектор , зокрема, кожен вектор базису переводить в вектор . Координатні рядки базисних векторів в базисі складають одиничну матрицю

,

3) Оператор подібності : має матрицю

.

Приклад. Лінійний оператор переводить вектор в вектор . Знайти матрицю оператора .

Розв’язання. Знайдемо образи векторів базису , , під дією оператора :

,

,

.

Координатні рядки векторів , , утворюють стовпці матриці оператора :

.

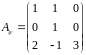Теорема. Нехай – лінійний оператор у векторному просторі , – його матриця. Тоді:

1. Ранг оператора збігається з рангом його матриці ;

2. Дефект оператора дорівнює різниці розмірності векторного простору , і рангу оператора ;

3. Сума рангу і дефекту оператора дорівнює розмірності векторного простору .

3. Дії з лінійними операторами

Оскільки дії лінійних операторів на вектор , заданий своїми координатами в певному базисі, визначаються у термінах операцій над матрицями, то дії з лінійними операторами можна звести до дій з матрицями.

Визначимо основні операції над лінійними операторами і паралельно згадаємо основні операції над матрицями

Нехай і – лінійні оператори у векторному просторі над полем , а і – відповідно їх матриці.

Означення. Лінійні оператори і називаються рівними, якщо для будь-якого вектора його образи при дії цих операторів рівні, тобто

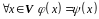
Рівні лінійні оператори в одному й тому самому базисі мають однакові матриці:

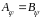
Означення. Сумою лінійних операторів і називається лінійний оператор , який будь-який вектор переводить в суму образів від дії на окремо операторів і , тобто

Матрицею суми лінійних операторів в фіксованому базисі є сума матриць операторів-доданків в тому ж базисі. Сумою матриць і розмірності називається матриця , де .

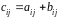Додавання лінійних операторів асоціативне, тобто вірна рівність

і комутативне, тобто вірна рівність

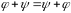
З урахуванням цих властивостей, а також наявності нульового оператора і протилежного для кожного оператора, заключаємо, що множина всіх лінійних операторів у векторному просторі є абелевою групою по додаванню.

Означення. Добутком лінійного оператора на число називається лінійний оператор , при дії якого образ будь-якого вектора множиться на число , тобто

При множенні лінійного оператора на число, його матриця множиться на це ж саме число: Добуток матриці на константу з поля виконується поелементно: .

Означення. Добутком лінійних операторів і називається лінійний оператор , який діє за правилом

Множення лінійних операторів не є алгебраїчною операцією, тому що воно визначено не для будь-якої пари операторів. Множення операторів, якщо воно виконується, має наступні властивості:

1. ;

2. ;

3. ;

4. 

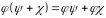
Матрицею добутку лінійних операторів в фіксованому базисі є добуток матриць операторів-множників в тому ж базисі.

Означення. Лінійною формою над кільцем з вектором змінних і фіксованими коефіцієнтами , , називається функція .

У випадку числових векторів лінійна форма – це скалярний добуток векторів. Зауважимо, що на відміну від скалярного добутку, тут можливий випадок , при . Це залежить від кільця .

Очевидно, якщо кільце є полем , функція є лінійним відображенням .

Добутком матриць розмірності і розмірності називається матриця розмірності , де , , .

У загальному випадку операція множення матриць некомутативна: . Операція множення матриць є асоціативною, якщо добутки, необхідні для виконання відповідних операцій, визначені.

В окремому випадку множення матриці-рядка на матрицю-стовпчик , результат визначається як .

В загальному випадку елемент матриці визначається як , де – рядок матриці з номером , а – стовпець матриці з номером .

Означення. Оберненим оператором до лінійного оператора називається лінійний оператор такий, що .

Матриця оператора , який має обернений, є квадратною невиродженою матрицею. Матриці операторів і є взаємно оберненими.

Матриця розмірності називається квадратною, якщо . Число називається її порядком.

Множина квадратних матриць порядку утворює некомутативне кільце. В цьому кільці нулем є нульова матриця , що складається з нулів. Одиницею є одинична матриця , в якої всі елементи головної діагоналі дорівнюють 1, а решта – 0.

Добуток квадратної матриці порядку на матрицю-стовпець можна розглядати як операцію над вектором. Ця операція є лінійним перетворенням -вимірного векторного простору. Квадратна матриця називається оборотною, якщо згадане лінійне перетворення є взаємно однозначним.

Нехай – оборотна матриця. Матрицею, оберненою до називається матриця , для якої виконується умови .