12

Динамика вращательного движения

Из опыта следует, что только сила F_ способна вызвать вращение тела вокруг закрепленной оси. Чем дальше от оси расположена точка приложения тангенциальной составляющей силы, тем легче осуществить поворот. Следовательно,

момент силы относительно оси характеризует способность силы вращать тело относительно данной оси.

Момент силы M относительно точки, в которой закреплено тело, характеризует способность силы вращать тело вокруг точки, относительно которой он берется. Причем поворот произойдет вокруг оси, параллельной вектору момента сил M.

При вращательном движении силовое воздействие характеризуется моментом силы, а не силой.

Момент инерции. 

Моментом инерции материальной точки массы m относительно оси называется величина, равная:

I = m·r²,        где r - кратчайшее расстояние от оси вращения до точки.

Момент инерции твердого тела равен сумме моментов инерции его частей:

I = m_i·r_i²     

Следовательно, момент инерции твердого тела зависит от:

	массы тела;
	формы и размеров тела;
	распределения массы относительно оси вращения (при переносе оси вращения или отдельных частей тела его момент инерции изменяется).

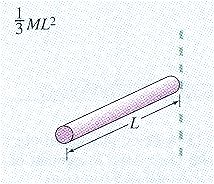
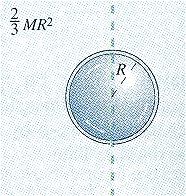
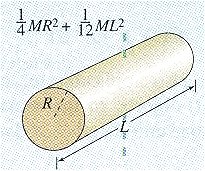
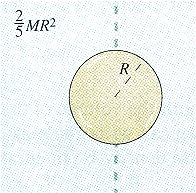
Для симметричных тел момент инерции рассчитывается с помощью интегрального исчисления. Моменты инерции некоторых симметричных тел приведены в таблице.

Д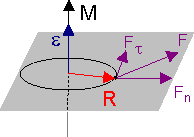 инамика вращательного движения материальной точки.

Рассмотрим частицу массы m, вращающуюся вокруг токи О по окружности радиуса R, под действием результирующей силы F (см. рис. 6.5). В инерциальной системе отсчета справедлив 2^ой закон Ньютона. Запишем его применительно к произвольному моменту времени:

F = m·a.

Нормальная составляющая силы не способна вызвать вращения тела, поэтому рассмотрим только действие ее тангенциальной составляющей. В проекции на тангенциальное направление уравнение движения примет вид:

F_= m·a_.

Поскольку  a_ = ·R, то

F_= m··R(6.6)

Умножив левую и правую части уравнения скалярно на R, получим:

F_·R= m··R²         (6.7) M = I·                (6.8)

Уравнение (6.8) представляет собой 2^ой закон Ньютона (уравнение динамики) для вращательного движения материальной точки. Ему можно придать векторный характер, учитывая, что наличие момента сил вызывает появление параллельного ему вектора углового ускорения, направленного вдоль оси вращения (см. рис. 6.5):

M = I·(6.9)

Основной закон динамики материальной точки при вращательном движении можно сформулировать следующим образом:

произведение момента инерции на угловое ускорение равно результирующему моменту сил, действующих на материальную точку.

Моменты инерции симметричных тел

Закон динамики вращательного движения твердого тела.

Обобщим полученный результат для твердого тела. Разобьем тело на элементарные участки массой m_i. Пусть r_i - расстояние от оси вращения до элемента массой m_i, а I_i - его момент инерции. Обозначим за M_i результирующий момент внешних сил, действующий на элемент m_i, а M_i^* - результирующий момент внутренних сил, действующий на него со стороны других элементов тела. Из уравнения (6.9) следует, что:

M_i + M_i^* = I_i·(6.10) где I_i - момент инерции элементарного участка тела относительно оси вращения.

Просуммировав уравнения (6.10) по всем элементам, и учитывая, что согласно 3^ему закону Ньютона суммарный момент внутренних сил равен нулю, получим уравнение, аналогичное (6.9):

M = I·(6.11) где M - суммарный момент внешних сил, действующих на твердое тело, относительно закрепленной точки О; I - момент инерции тела относительно оси вращения.

Следовательно, основной закон динамики вращательного движения твердого тела относительно закрепленной точки можно сформулировать следующим образом:

произведение момента инерции тела на его угловое ускорение равно суммарному моменту внешних сил, действующих на тело. Моменты сил и инерции берутся относительно оси, вокруг которой происходит вращение.

В случае движения тела относительно закрепленной оси необходимо спроецировать уравнение (6.11) на эту ось.

M _z = I_z·.     (6.12)

Из уравнения (6.12) можно найти какое угловое ускорение относительно закрепленной оси приобретет тело под действием момента сил M_z.

Условия равновесия твердого тела.

Тело находится в равновесии, если оно не обладает ускорением поступательного и вращательного движений, т.е. выполняются следующие условия: a = 0,  = 0. Очевидно, что это имеет место при равенстве нулю результирующей силы и суммарного момента внешних сил. Следовательно, в условии равновесия выполняются равенства: F = 0 и M = 0.

Заметим, что равенство нулю результирующего вектора сил, действующих на тело, не обязательно обуславливает равенство нулю суммарного момента внешних сил. Типичным примером является момент пары сил, вызывающего движение тела с угловым ускорением (см. рис. 6.6). Расстояние между линиями продолжения сил l  называется плечом пары. Момент пары сил равен:

M = [R₁₂·F], где R₁₂ - вектор расстояния между точками приложения сил.

Абсолютное значение момента пары сил равно:

|M| = l·F.

Кинетическая энергия вращающегося тела. Теорема Штейнера.

Кинетическая энергия твердого тела при вращательном движении.

Кинетическая энергия твердого тела складывается из кинетических энергий его частей E_i. Рассчитаем значение E_i для элементов твердого тела.

E_i = m_i·v_i²/2 = m_i·w²·r_i²/2.

Кинетическая энергия твердого тела будет равна:

E_к = w²/2·m_i·r_i² = I·w²/2.      (8.13)

Заметим, что формула для расчета E_к похожа на выражение для определения кинетической энергии поступательного движения тела, только роль меры инертности в этом случае играет момент инерции, а не масса и характеристикой движения является угловая, а не линейная скорость твердого тела.

Работа при вращательном движении твердого тела.

Рассчитаем работу силы, вызывающей вращательное движение тела вокруг некоторой оси и приложенной к произвольной точке этого тела. Согласно определению работы имеем:

A = F·ds = F_·ds. 

Поскольку ds = r·d, то получим следующее выражение для работы:

A = F_·r·d = M·d.

При вращательном движении твердого тела под действием силы F работа равняется произведению момента этой силы на угол поворота.

Работа переменной силы при повороте тела на конечный угол равняется определенному интегралу от момента сил:

  .

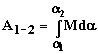Покажем, работа, совершаемая под действием равнодействующего момента сил, равна изменению кинетической энергии тела. Действительно,

A = M·d= I··d = I·(dw/dt)·w·dt = I·d(w²/2), где M - суммарный момент всех сил, действующих на тело.

Произведя интегрирование по углу, получим:

 A₁₂ = I·w₂²/2 - I·w₁²/2 = E_к.

Кинетическая энергия твердого тела, совершающего вращательное и поступательное движения.

Любое произвольное движение твердого тела можно представить в виде суммы поступательного движения центра масс тела и вращательного движения в СО, связанной с этим центром масс. Проанализируем движение тела относительно двух таких систем: СО, связанной с центром масс тела - точкой С, и инерциальной СО - системой XY, относительно которой перемещается центр масс (см. рис. 6.7). Любая точка тела участвует в двух движениях: поступательном, происходящим в данный момент времени со скоростью V_c, и вращательном, происходящим с угловой скоростью  w' = v_i'/R_i, относительно точки С. 

Скорости тела в этих системах связаны между собой известным соотношением:

v_i = V_c + v_i', где v_i - скорость i^ой части в ИСО; V_c - скорость движения центра масс тела; v_i' - скорость i^ой части в СО, связанной с центром масс.

Можно показать, что

кинетическая энергия твердого тела состоит из кинетической энергии его поступательного движения и энергии его движения E' = I·w²/2 относительно СО, связанной с центром масс тела.  Это утверждение называется теоремой Кёнига. E_к = E' + M·V_c²/2.

Теорема Кёнига справедлива для любого плоского движения при котором центр масс перемещается в некоторой фиксированной плоскости, а вектор угловой скорости все время перпендикулярен к этой плоскости. Примером плоского движения является качение.

Т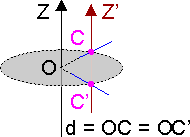 еорема Штейнера.

Рассмотрим вращение стержня вокруг некоторой оси Z (см. рис. 6.8). Кинетическую энергию стержня можно представить в виде:

E_к = I·w²/2. где I - момент инерции стержня относительно оси Z.

С другой стороны, согласно теореме Кёнига, эту энергию можно найти как сумму кинетических энергий поступательного движения по окружности радиуса d центра масс тела (точки С) и вращательного движения стержня относительно оси Z':

E_к = m·V_c²/2 + I_c·w²/2, где I_c - момент инерции стержня относительно оси Z'.

Учитывая, что для случая движения по окружности справедливо соотношение V_c = d·w, и приравнивая приведенные выше выражения для кинетической энергии стержня, получим уравнение, которое является выражением теоремы Штейнера:

I = I_c + m·d²/2.

Момент инерции тела относительно произвольной оси вращения равен его моменту инерции относительно параллельной оси, проходящей через центр масс тела, плюс произведение массы на квадрат расстояния между этими осями.

Пример. Тонкий стержень, вращающийся вокруг оси, направленной перпендикулярно к его длине.

Тело	Положение оси вращения	Момент инерции
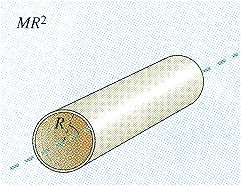
Полый тонкостенный цилиндр радиуса R	Ось симметрии
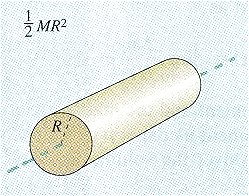
Сплошной цилиндр или диск радиуса R	То же
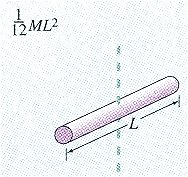
Прямой тонкий стержень длиной l	Ось перпендикулярна стержню и проходит через его середину
Прямой тонкий стержень длиной l	Ось перпендикулярна стержню и проходит через его конец
Шар радиусом R	Ось проходит через центр шара

В табл. 4.2 сопоставлены основные физические величины и уравнения, определяющие вращение тела вокруг неподвижной оси и его поступательное движение.  

Поступательное движение	Вращательное движение
Масса  m	Момент инерции Jz
Скорость	Угловая скорость
Ускорение	Угловое ускорение
Сила	Момент силы
Импульс	Момент импульса
Основное уравнение динамики:	Основное уравнение динамики:
Работа	Работа вращения
Кинетическая энергия	Кинетическая энергия вращения