
- •Раздел 1. Проектирование и кинематический анализ
- •Раздел 2. Силовой расчет механизма
- •Введение
- •1.Проектирование и кинематический анализ
- •1.1. Построение крайних положений звеньев механизма.
- •1.2. Построение промежуточных положений механизма
- •1.3. Кинематический анализ исходного звена
- •1.4. Построение планов скоростей для 2-х положений механизма.
- •1.5. Построение планов ускорений для 2-х положения механизма.
- •Раздел 2. Силовой расчет механизма.
- •2.1. Силовой расчет кинематической пары звеньев 2-3.
- •2.2 Силовой расчет ведущего звена.
- •Список литературы
2.1. Силовой расчет кинематической пары звеньев 2-3.
Силовой расчет механизма ведем для положения 1, к которому построен план ускорений. Зарисовываем группу в масштабе μl=0,001 м/мм, сохраняя положения звеньев, прикладывая Рпс=0Н. Прикладываем также, силы веса
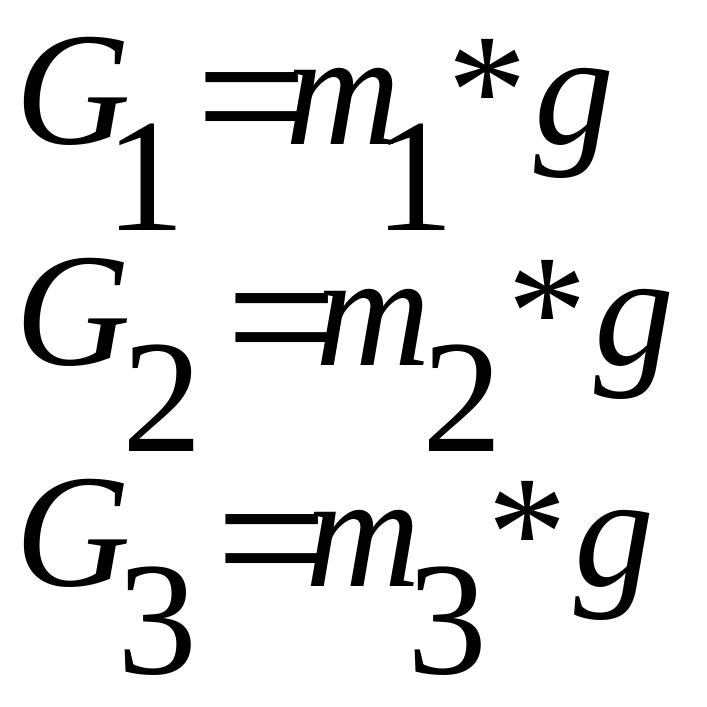 ,
(2.1)
,
(2.1)
где
![]() масса
звена, кг
масса
звена, кг
![]() ускорение
свободного падения,
ускорение
свободного падения,
![]() ,
,
силы инерции:
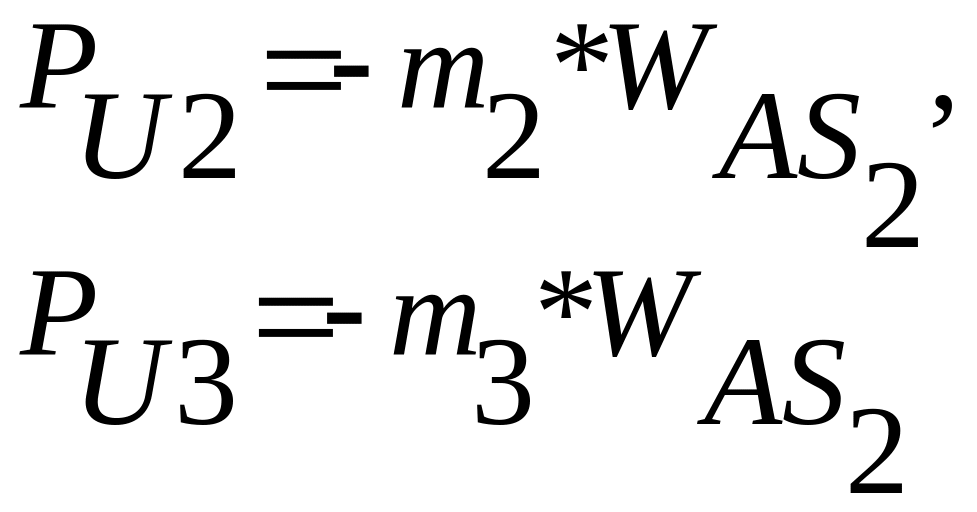 (2.2)
(2.2)
со
стороны отброшенных звеньев в
поступательной паре прикладываем
неизвестную реакцию
![]() перпендикулярно направляющей ползуна
и в шарнире А прикладываем также
неизвестную реакцию
перпендикулярно направляющей ползуна
и в шарнире А прикладываем также
неизвестную реакцию
![]() ,
которую можно разложить на составляющие
согласно равенству:
,
которую можно разложить на составляющие
согласно равенству:
![]()
![]() , (2.3)
, (2.3)
где
![]() направляется перпендикулярно линии
звена АВ, а
направляется перпендикулярно линии
звена АВ, а
![]() параллельна этой линии.
Определяем
тангенциальную составляющую
,
составляя уравнение звена 2 в форме
моментов относительно точки В:
параллельна этой линии.
Определяем
тангенциальную составляющую
,
составляя уравнение звена 2 в форме
моментов относительно точки В:
![]() (2.4)
(2.4)
![]() ,
(2.5)
,
(2.5)
где
![]() -плечо
силы
-плечо
силы
![]() ,
равное
,
равное
![]() μl*
μl*![]() ,
,
![]() -
плечо силы веса, равное
-
плечо силы веса, равное
![]() =
μl*
=
μl*![]() ,
,
![]() -момент
силы инерции, Н*м,
-момент
силы инерции, Н*м,
![]() ,
(2.6)
,
(2.6)
где
![]() -
момент инерции относительно центра
масс S
-
момент инерции относительно центра
масс S![]() звена 2,
звена 2,
![]() -
угловое ускорение звена,
-
угловое ускорение звена,
![]() ;
;
![]() -
длина звена 2.
-
длина звена 2.
Точное направление
![]() определиться знаком полученного
результата , при отрицательном результате
направление следует принять за
противоположное.
определиться знаком полученного
результата , при отрицательном результате
направление следует принять за
противоположное.
Для того, чтоб
определить
![]() и
,
запишем уравнение равновесия все группы
в векторной форме:
и
,
запишем уравнение равновесия все группы
в векторной форме:
![]() (2.7)
(2.7)
Векторы сил,
известные по величине и направлению,
подчеркнуты двумя чертами, известные
только по направлению линии действия
одной, в данном случае это силы
и
![]() .
.
Для построения
плана сил определяем масштабный
коэффициент плана сил
![]() ,
а отрезки, выражающие векторы сил на
плане, получаются делением натуральных
значений сил на плане на масштаб на
плане. Размещая векторы
и
радом,
находим точку их пересечения, которая
определяет величины этих векторов и их
точные направления, а соединив начало
,
а отрезки, выражающие векторы сил на
плане, получаются делением натуральных
значений сил на плане на масштаб на
плане. Размещая векторы
и
радом,
находим точку их пересечения, которая
определяет величины этих векторов и их
точные направления, а соединив начало
![]() с концом
,
определяем вектор
с концом
,
определяем вектор
![]() полной реакции в шарнире А.
полной реакции в шарнире А.
2.2 Силовой расчет ведущего звена.
Зарисовываем звено в масштабе μl=0,002м/мм , прикладывая в точку А
известную
реакцию
![]() (которая
равна и противоположна по направлению
(которая
равна и противоположна по направлению
![]() ).
Уравновешивающую силу прикладываем в
точке А перпендикулярно звено
).
Уравновешивающую силу прикладываем в
точке А перпендикулярно звено
![]() ,
ее плечом
,
ее плечом
![]() будет длина кривошипа. Освобождаем
звено от связей со стойкой и
прикладываем вместо нее реакцию
будет длина кривошипа. Освобождаем
звено от связей со стойкой и
прикладываем вместо нее реакцию
![]() .
.
Запишем векторное уравнение сил, действующих на ведущее звено:
![]() (2.9)
(2.9)
Из всех сил
действующих на кривошип, неизвестными
являются величина
![]() и величина и направление реакции
.
На кривошип также действует сила веса
и величина и направление реакции
.
На кривошип также действует сила веса
![]() в центре масс
в центре масс
![]() ,
который совпадает с точкой
,
который совпадает с точкой
![]() .
Уравновешивающую силу
целесообразно определить из уравнения
равновесия кривошипа в форме моментов
относительно точки
.
Уравновешивающую силу
целесообразно определить из уравнения
равновесия кривошипа в форме моментов
относительно точки
![]() (2.10)
(2.10)
где
![]() ,
,
![]()
Решая уравнение (2.11) относительно получаем
![]() 7742
Н,
7742
Н,
Решая уравнения
(2.9) строим план сил, в предварительно
выбранном масштабе
![]() и определим
из него вектор искомой реакции
.
По правилу сложения векторов этот вектор
направлен к началу
и определим
из него вектор искомой реакции
.
По правилу сложения векторов этот вектор
направлен к началу
![]() .
.
ЗАКЛЮЧЕНИЕ
При выполнении первого раздела курсового проекта был проведен кинематический анализ механизма методом планов. Во втором разделе рассмотрены построение планов сил, действующих на звенья реакции в кинематических парах, определена уравновешивающая сила методом планов.
