П равило дослідження функції f(X) на монотонність та екстремум:

1.	Знайти ОВФ f(x)
2.	Знайти першу похідну
3.	Знайти критичні точки 1-го роду функції f(x) і, розмістивши їх в порядку зростання, нанести на ОВФ
4.	Записати інтервали монотонності, на які критичні точки разом з точками розриву функції ділять ОВФ.
5.	За знаком похідної встановити, зростає чи спадає функція на кожному інтервалі.
6.	Скориставшись першою достатньою ознакою екстремуму, знайти екстремальні точки.
7.	Обчислити екстремальні значення функції.

Приклад 1. Знайти інтервали монотонності та дослідити на екстремум функцію

Розв’язання. Використаємо вище наведене правило. 1) ОВФ: 2) Знаходимо похідну

3) Знаходимо критичні точки 1-го роду:

а ) – стаціонарна точка;

б ) коли знаменник дробу дорівнює нулю, тобто коли – критична точка. Зазначимо, що в цій точці похідна терпить розрив, а сама функція визначена і неперервна. Інших критичних точок немає. 4) Відмічаємо критичні точки на ОВФ (д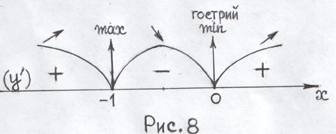 ивись рис. 8) Інтервали монотонності:

5) Визначаємо знак похідної на кожному інтервалі за знаком похідної у пробній точці інтервалу:

– функція зростає на ;

– функція спадає на (–1;0);

– функція зростає на

6) При переході через стаціонарну точку похідна змінює знак з «+» на «–», отже точка – точка круглого максимуму. При переході через критичну точку похідна змінює знак з

«–» на «+», тому точка – це точка гострого мінімуму (дивись рис. 8) . 7) Обчислимо екстремальні значення функції:

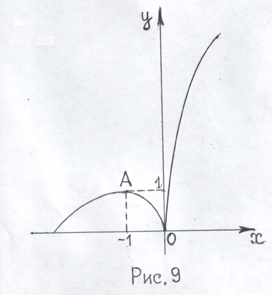
А(-1;1) і О(0;0) – точки на графіку

функції, де вона має max і min відповідно.

8) Будуємо ескіз графіка функції (дивись рис.9).

У більш– менш складних прикладах визначити знак похідної у пробних точках досить трудно. Щоб «обійти» ці труднощі, в окремих випадках можна скористатися іншим способом дослідження функції на екстремум. Сформулюємо так звану другу достатню ознаку екстремуму, яка інколи виявляється зручнішою і простішою, ніж перша достатня ознака.

Друга достатня ознака екстремуму (друге правило). Нехай в околі стаціонарної точки існує неперервна друга похідна функції f(x), причому Тоді

Якщо то – точка min функції f(x);

Якщо то – точка max функції f(x).

При у точці може бути або max, або min,або ж не буде ні max, ні min. Потрібні додаткові дослідження.

Унаочнює другу достатню ознаку так зване правило «ковшика»:

Правило знаходження екстремуму функції за допомогою другої похідної:

1.	Знайти першу похідну .
2.	Знайти стаціонарні точки даної функції, тобто точки, в яких
3.	Знайти другу похідну .
4.	Дослідити знак другої похідної в кожній з стаціонарних точок. Якщо при цьому друга похідна буде додатною, то функція в такій точці має min, а якщо від’ємною, то max.
5.	Обчислити значення функції в точках екстремуму.

Приклад 2. Дослідити на екстремум функцію

Розв’язання. 1) Задана функція всюди неперервно диференційовна. Знайдемо її першу похідну:

2) Шукаємо стаціонарні точки із умови

Стаціонарні точки будуть такими:

3) Знайдемо другу похідну:

4) Досліджуємо знак другої похідної в стаціонарних точках:

Отже, Тому, згідно з другого правилом у стаціонарних точках та функція досягає максимуму.

5) Обчислимо екстремальні значення функції:

Примітка. Що стосується стаціонарної точки то нічого конкретного поки сказати неможливо. Для її дослідження потрібно скористатися першою достатньою ознакою. Доходимо висновку, що друге правило застосовне для вужчого класу функцій , ніж перше.