2.4.2. Точкові оцінки математичного сподівання і дисперсії
Нехай
– деяка статистична оцінка, одержана
по вибірці
,
і яка оцінює невідомий параметр
розподілу генеральної сукупності. Якщо
оцінка визначається одним числом
,
то
її
називають
точковою;
якщо
обчислюються
дві величини
і
такі, що
,
то оцінку для
називають інтервальною,
а величини
,
– границями
інтервалу.
Нехай випадкова
величина X (генеральна
сукупність) має математичне сподівання
і дисперсію
Обидва ці параметри невідомі. Над X
проводяться n спостережень
і добувається вибірка
.
Необхідно знайти незміщені і слушні
оцінки параметрів
і
.
За оцінку математичного сподівання природно прийняти вибіркове середнє :
.
(2.25)
Ця оцінка є слушною:
згідно з законом великих чисел
збігається за ймовірністю до
.
Оцінка
є також і незсуненою, оскільки:
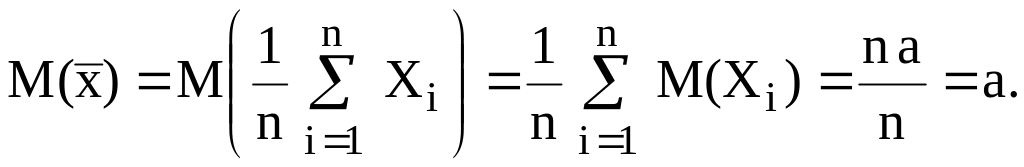
У випадку нормального
розподілу з параметрами
оцінка
,
як було сказано раніше, також і ефективна.
Дійсно
,
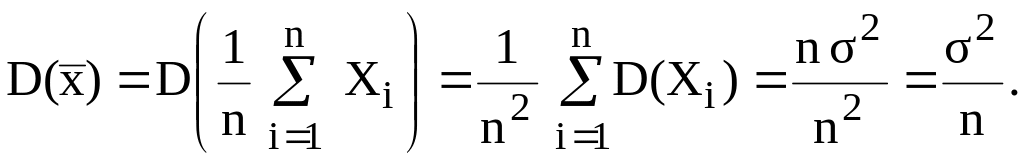
Для обчислення
ефективності визначимо ще величину
для
.
Покладаючи
знаходимо
За формулою для ефективності оцінки знаходимо
Отже, оцінка математичного сподівання нормального розподілу є ефективною.
Визначимо тепер
дисперсію
За оцінку
візьмемо вибіркову дисперсію:
(2.26)
Ця оцінка є слушною. Щоб це показати, приведемо її до вигляду:
,
де .
Оскільки згідно з законом великих чисел
,
,
Що й означає слушність оцінки . Знайдемо математичне сподівання :
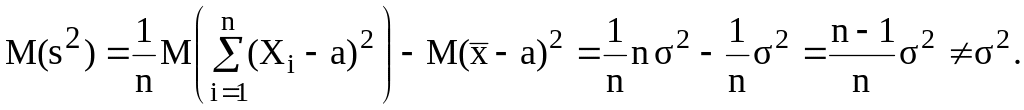
Тут
використаний той факт, що
Таким
чином оцінка
є зміщеною оцінкою дисперсії генеральної
сукупності. Щоб ліквідувати зсуненність,
потрібно ввести поправку
.
Одержуємо:
(2.27)
Цю
оцінку називають виправленою
вибірковою дисперсією.
Вона є незсуненою і слушною. Величину
називають поправкою Бесселя. При малих
n
ця поправка значно відрізняється від
одиниці. При збільшенні n
вона швидко прямує до одиниці та при
практично дорівнює одиниці.
У
загальному випадку оцінка
дисперсії не є ефективною. Для нормального
розподілу ефективність її дорівнює
;
таким чином, при
вона асимптотично
ефективна.
2.4.3. Методи знаходження оцінок параметрів розподілу
Припускається,
що невідома функція розподілу належить
деякому сімейству розподілів
,
яке залежить від деякого параметра
(параметр
,
можливо, векторний
Так, наприклад, сімейство нормальних
розподілів залежить від двох параметрів
– математичного сподівання і дисперсії.
Потрібно за результатами спостережень
(значенням вибірки) оцінити параметр
(або декілька параметрів) розподілу.
Для побудови оцінок використовуються статистики функції від вибіркових значень. Розповсюдженими статистиками є:
вибіркова середня ;
вибіркова дисперсія ;
вибірковий k-й початковий момент
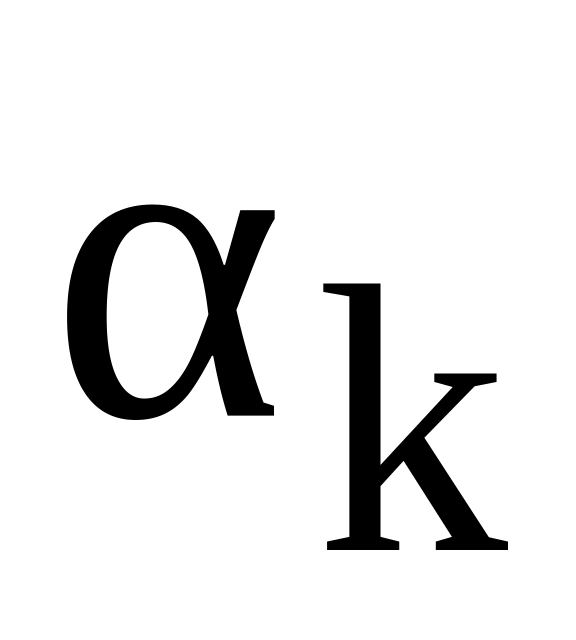;вибірковий k-й центральний момент
;
Оскільки результати спостережень випадкові, будь-яка статистика представляє собою випадкову величину. Для того, щоб статистика могла служити оцінкою даного параметра , необхідно, щоб розподіл цієї статистики був зосереджений у достатній близькості від невідомого значення параметра , тобто, щоб імовірність великих відхилень цієї статистики від була достатньо мала. Бажано також, щоб точність оцінювання зростала при збільшенні об’єму вибірки. Для цього оцінка повинна мати вказані раніше властивості незсуненності, слушності і ефективності.
Розглянемо основні методи знаходження оцінок.