2.5.2. Надійний інтервал для математичного сподівання нормального розподілу a при відомому σ

При великому об’ємі вибірки (n→∞) розподіл вибіркових характеристик (статистик) необмежено наближається до нормального (практично при розподіл вибіркової середньої можна вважати приблизно нормальним).

Статистична модель. Нехай генеральна сукупність (випадкова величина Х) розподілена нормально з невідомим математичним сподіванням а і відомим середнім квадратичним відхиленням . Треба оцінити невідоме математичне сподівання a (генеральне середнє арифметичне) за вибірковим середнім і знайти надійний інтервал з довірчою ймовірністю .

Для повторної вибірки вибіркові значення є незалежні випадкові величини, розподілені як і величина (генеральна сукупність) за нормальним законом. Відносно випадкових величин і відомо наступне:

• математичне сподівання 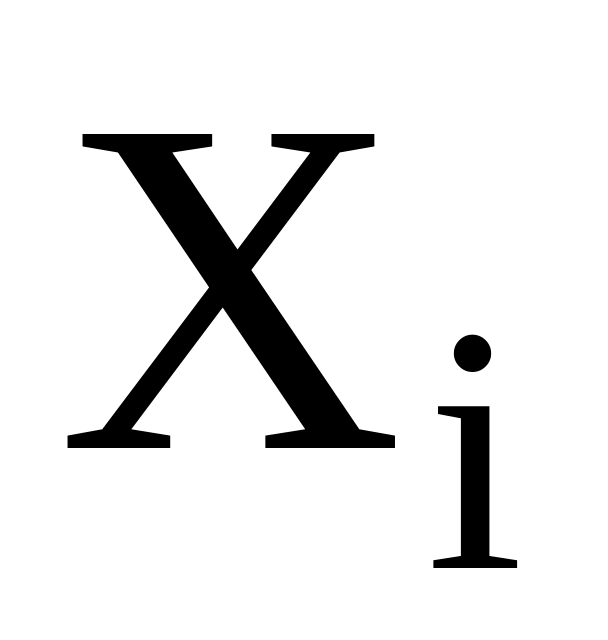дорівнює а, дисперсія :

, = .

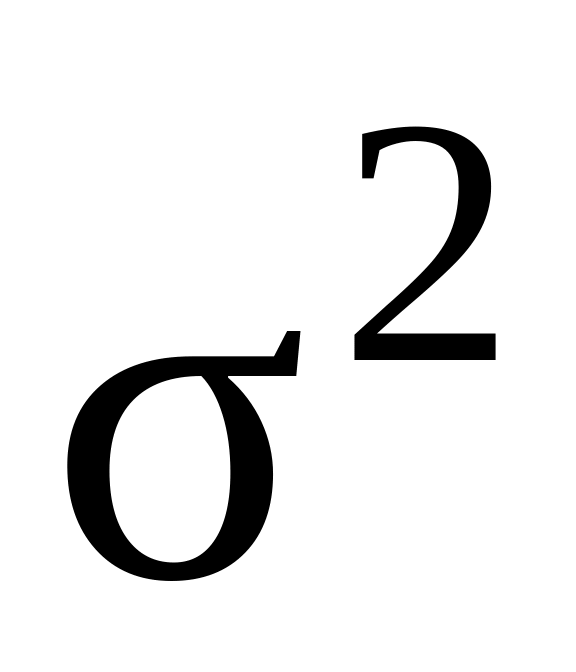• оскільки величини 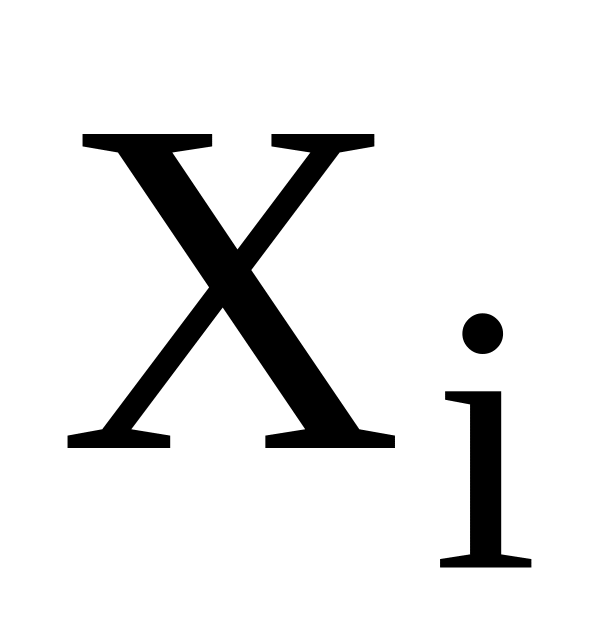розподілені нормально, то і їх сума (середнє арифметичне)

також розподілена за нормальним законом з параметрами

.

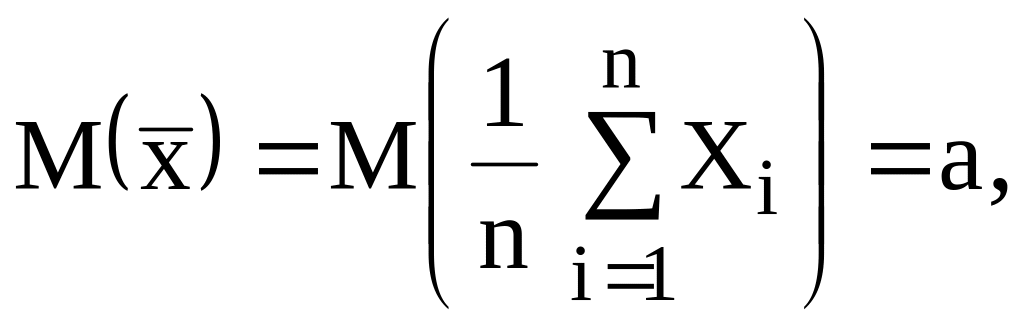
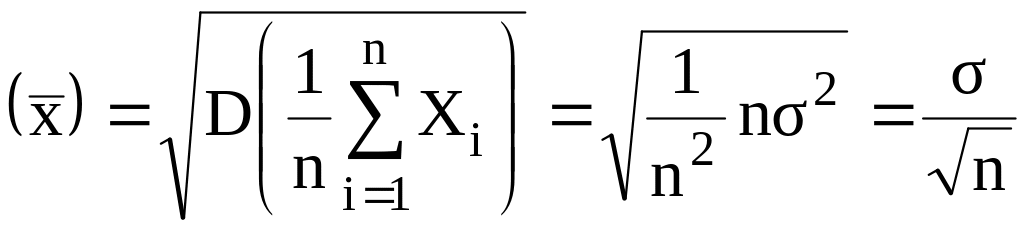• випадкова величина 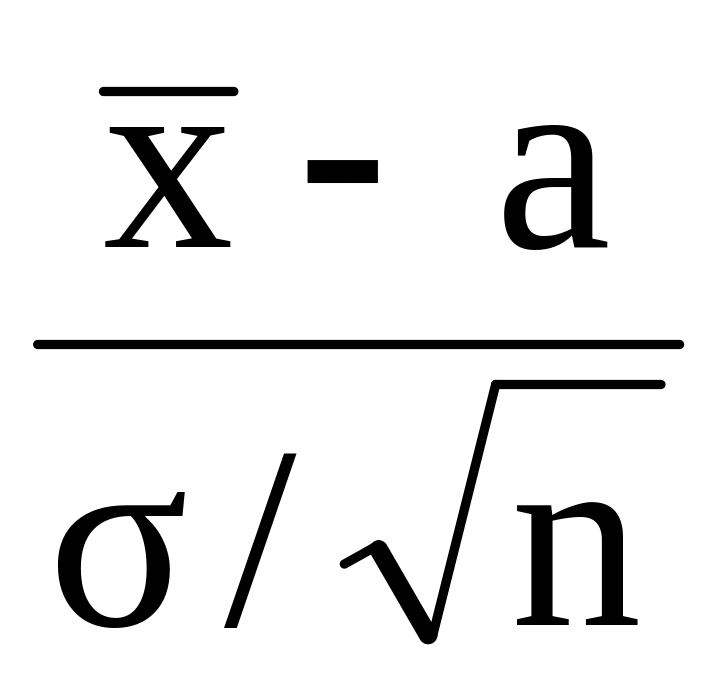розподілена за нормальним законом 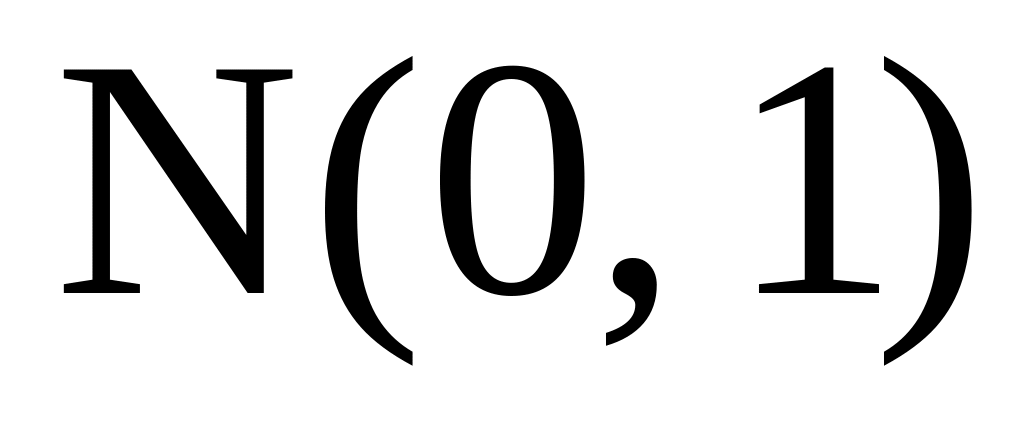з параметрами 0 і 1 і розподіл не залежить від оцінюваного параметра а.

Задамо надійну ймовірність і визначимо величину із рівняння

.

Оскільки нормально розподілена величина з параметрами a і , то ймовірність того, що буде дорівнювати

(2.39)

де – функція Лапласа (інтеграл ймовірностей), а дорівнює:

. (2.40)

Величину визначаємо із рівності

або

де рівень значущості.

У Mathcad визначається як квантиль нормованого нормального розподілу порядку за функцією qnorm( ):

(2.41)

Знайшовши із формули (2.41), визначаємо граничну похибку оцінки :

. (2.42)

Обчисливши , одержуємо, що із імовірністю виконана нерівність

або (2.43)

На рис 2.3 показано, що випадкова величина , яка має стандартний нормальний розподіл, з імовірністю приймає значення, що попадають в інтрервіл , отже, з імовірністю виконується нерівність (2.43).

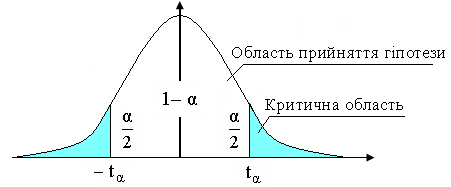
Рис. 2.3. Надійний інтервал для математичного сподівання

Таким чином, інтервал є надійним інтервалом для математичного сподівання нормального розподілу. Смисл цього співвідношення такий: з надійністю можна стверджувати, що надійний інтервал покриває невідоме середнє арифметичне генеральної сукупності.

Для безповторної вибірки об’єму n із генеральної сукупності об’єму N, представляє собою суму залежних випадкових величин. Однак і в цьому випадку при n→∞ закон розподілу як завгодно близько наближається до нормального. При цьому середнє квадратичне відхилення дорівнює

,

значення якого підставляється у (2.42.). Отже, і для безповторної вибірки надійний інтервал для a має вигляд (2.43).

Формула (2.42) зв’язує між собою три величини: надійну ймовірність , граничну похибку вибірки і об’єм вибірки n. У кожній конкретній задачі дві із цих величин задаються і визначається третя. У результаті одержуємо три типи задач:

1. Дані n і , визначається .

2. Дані n і , визначається .

3. Дані і , визначається n.

Перші дві задачі зв’язані з аналізом результатів вже зробленої вибірки даного об’єму n, отже, і із заданою точковою оцінкою .

Ціллю розв’язання задач третього типу є розрахунок необхідного об’єму вибірки n, який забезпечить задану граничну похибку вибірки при вибраній величині надійної ймовірності

Перша задача – визначення точності оцінки δ – є задача побудови надійних інтервалів для оцінок параметрів розподілів, що розглядалась вище. Розглянемо тепер другу і третю задачі.

Алгоритм визначення надійної ймовірності γ

Якщо заданий об’єм вибірка n і гранична похибка вибірки і необхідно визначити надійну ймовірність γ, то алгоритм розв’язку задачі наступний :

• за формулою (2.40) визначаємо ;

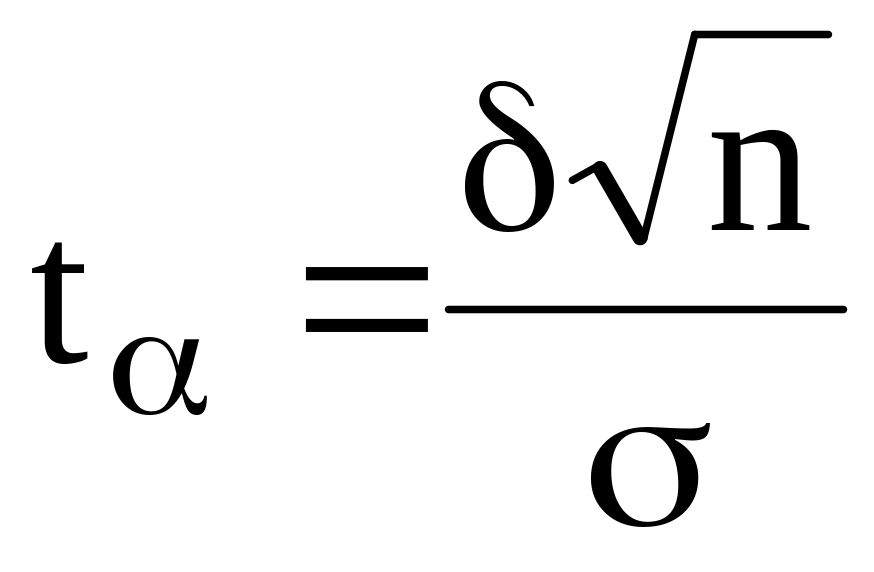• імовірність знаходимо за формулою .

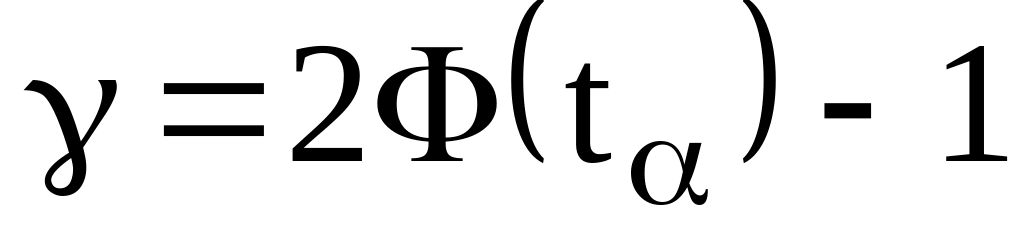Алгоритм визначення об’єму вибірки:

Встановлення об’єму вибірки n для проведення вибіркових спостережень є важливим, оскільки це визначає необхідні при цьому часові, трудові і вартісні витрати. Для визначення n необхідно задати: надійну ймовірність (надійність оцінки) і граничну похибку оцінки (точність оцінки). Із формули (2.42) одержуємо :

. (2.44)

Якщо вибірка безповторна, то об’єм вибірки із генеральної сукупності об’єму N визначається за формулою :

. (2.45)

Якщо знайдений об’єм повторної вибірки n, то об’єм безповторної вибірки можна визначити за формулою :

. (3.47)

Оскільки , то при одній і тій же точності і надійності оцінок, об’єм безповторної вибірки завжди менший об’єму повторної вибірки n. Цим пояснюється той факт, що на практиці в основному використовується безповторна вибірка.

Припускається, що математичне сподівання розподілу генеральної сукупності невідоме, але відома її дисперсія .

Коментар. Цей метод стійкий при помірних відхиленнях розподілу від нормальності.

Алгоритм побудови надійного інтервалу

1. Обчислюється точкова оцінка математичного сподівання

2. Задається рівень значущості оцінки .

3. Із рівності де – функція стандартного нормального розподілу, обчислюється квантиль , – функція обернена до функції . У Mathcad квантиль нормованого нормального розподілу обчислюється за функцією qnorm ( ).

4. Обчислюється точність оцінки .

5. Обчислюється надійний інтервал: .

Приклад 2.6. Вибірка об’єму одержана із генеральної сукупності, розподіленої за нормальним законом з невідомим математичним сподіванням а і відомим середнім квадратичним відхиленням . Треба оцінити невідоме генеральне середнє арифметичне (математичне сподівання ) за вибірковим середнім і знайти надійний інтервал з імовірністю .

Розв’язання. Змоделюємо вибірку об’єму у припущенні, що генеральна сукупність розподілена за нормальним законом з параметрами . Вибірку моделюємо за допомогою функції . Обчислення проводимо за наступним алгоритмом.

Алгоритм у Mathcad

_{Початкові дані моделі}

_{Моделювання вибірки із нормально розподіленої генеральної сукупності}

_{Фрагмент вибірки}

_{Вибіркове середнє арифметичне і середнє квадратичне відхилення}

Квантиль нормованого нормального розподілу порядку

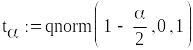
_{Точність оцінки математичного сподівання}

Границі надійного інтервалу

Надійний інтервал для математичного сподівання а

◄