Вывод формул для дисперсий коэффициентов регрессии и расчетных значений

Приведем систему исходных предпосылок регрессионного анализа (гипотезы Гаусса–Маркова) в порядке убывания их важности:

1. y_i = h(x_i) + e_i ; Все случайные ошибки относятся только к у; h(x_i) – известная функция.

2. M(e_i) = 0;       Систематических ошибок нет; .

3. ;   Наблюдения равноточны (гомоскедастичность – одинаковый разброс).

4. M(e_ie_j) = 0;    Наблюдения не коррелированы (не зависимые).

5. e_i ~ N(0; s_e);  Ошибки распределены нормально (самая несущественная предпосылка).

По исходным данным (x_i, y_i) вычислены некоторые числовые характеристики: . Первые две из этих характеристик считаются измеренными точно, поскольку все случайные ошибки относятся только к переменной y. Остальные же характеристики содержат случайную ошибку, поэтому они сами являются случайными величинами с известным законом распределения (такие характеристики называются “статистиками”).

Рассмотрим первую статистику из вышеприведенного списка:

Поскольку все (вторая гипотеза), то .

Вычисляем дисперсию :

.

Здесь использовано:

;

свойства математического ожидания;

для i ¹ j (четвертая гипотеза);

(третья гипотеза).

Мы получили известный факт – случайная дисперсия среднего арифметического в n раз меньше случайной дисперсии отдельных наблюдений.

Теперь рассмотрим коэффициент регрессии b₁ :

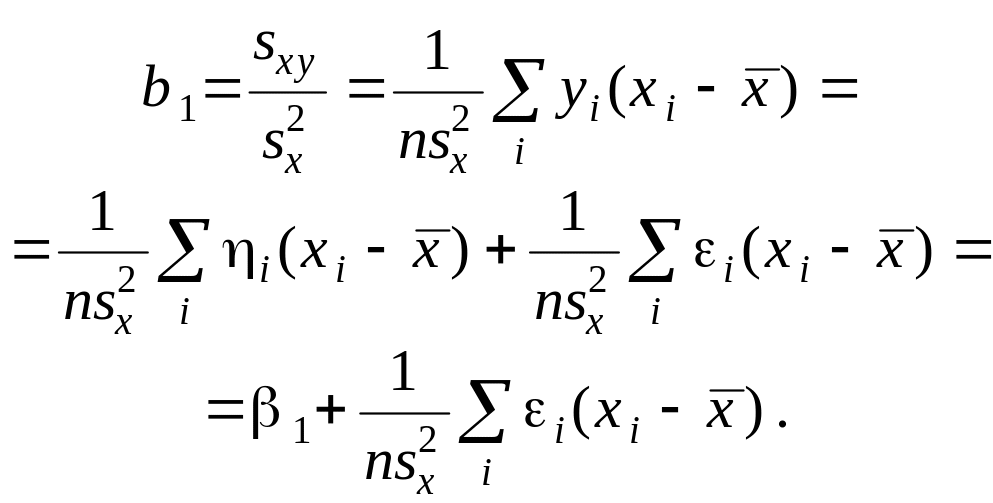
Здесь b₁=M(b₁) получается по той же формуле, что и b₁ с заменой y_i на h_i .

Вычисляем дисперсию :

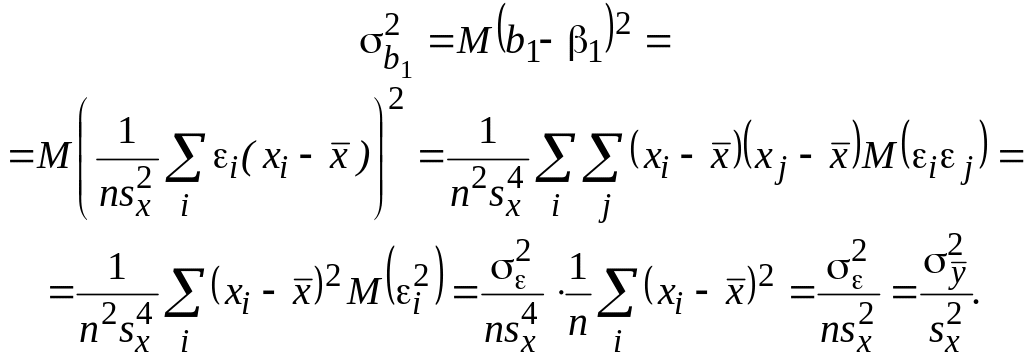
Покажем, что ковариация равна нулю:

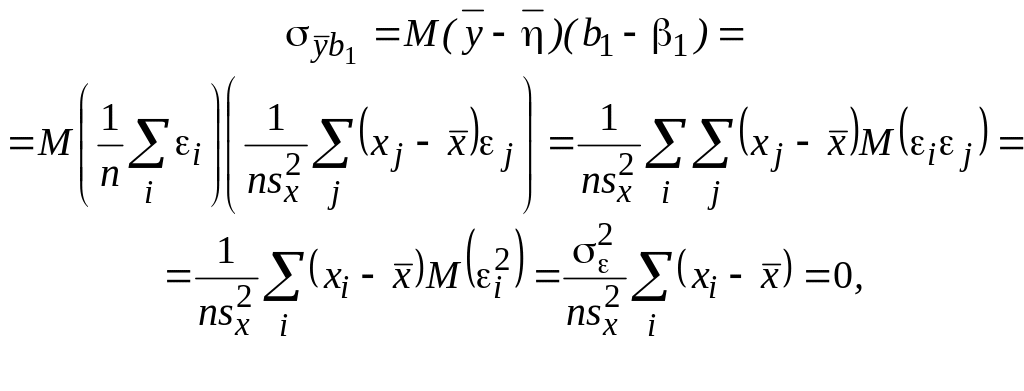
т.к.

Расчетное значение y_p для каждого x оказывается комбинацией двух случайных величин и b₁:

.

Вычисляем его дисперсию по известному свойству дисперсии суммы:

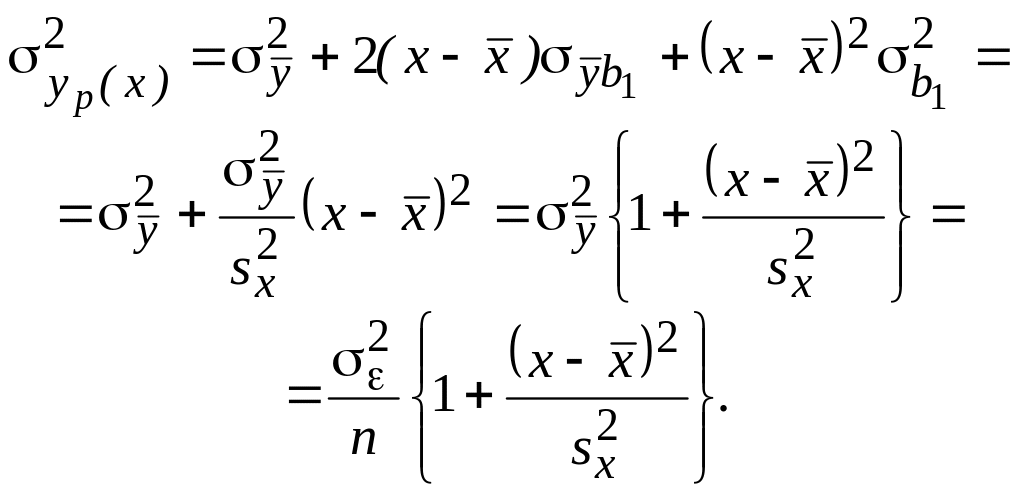
Осталось заменить дисперсию случайной ошибки на несмещенную дисперсию остатка модели:

.

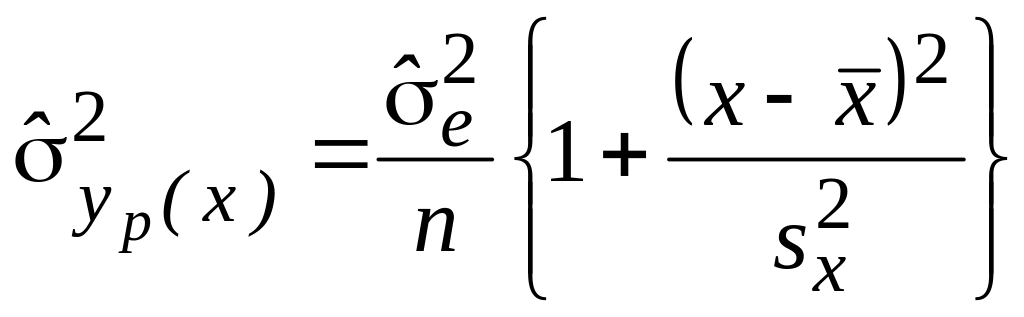Вопросы для самопроверки

1. Что такое "стандартизованные переменные"? Каковы из свойства?

2. Что такое "-коэффициенты"? Как они связяны с коэффициентами регрессии? Чему равно ₀ ?

3. Какой вид имеет система нормальных уравнений в стандартизован­ных переменных?

4. Как в стандартизованных переменных записывается выражение для коэффициента детерминации?

4. Как оценивается значимость модели в целом и значимость ее отдельных членов?

5. Как записать интервальные оценки для коэффициентов регрессии:

6. Как строится доверительная полоса на расчетные значения? Что она показывает?

7. Как составляется многофакторная регрессионная модель?

8. Что такое "коэффициенты частной корреляции"?

9. Каков общепринятый критерий качества регрессионной модели?

156