Коэффициенты частной корреляции

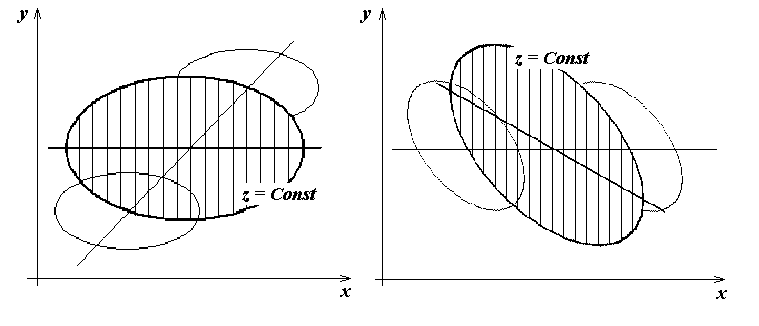
Неконтролируемая изменчивость переменных, которые не учтены в модели, может полностью исказить изучаемые корреляционные связи. На рис. 16.3 изображены две типичные ситуации, когда проявляется этот неприятный эффект. Рис. 16.3 (а) демонстрирует эффект появления ложной корреляции между показателями x, y. При любом фиксированном значении третьего показателя z облако рассеивания емпирических точек вытянуто вдоль координатной оси x, следовательно, никакой кореляционной связи между x и y нет. Но с изменением неконтролируемого показателя z облако рассеивания данных сдвигается вдоль некоторой наклонной линии (в координатах x, y), в результате чего по всей совокупности данных проявляется кореляционная зависимость, поскольку большим значениям одной из переменных (x) в среднем соответствуют большие значенни другой переменной (y).

а б

Рис. 16.3. Влияние неконтролируемой изменчивости показателя z на корреляционную зависимость между x и y

На рис. 16.3 (б) показано, как неконтролированная изменчивость показателя z может скрыть существующую корелряционную зазависимость между x и y. Общее (сумарное) облако рассеивания точек тут оказалось вытянутым вдоль оси x, что означает отсутствие корреляционной связи по всей совокупности данных.

Чаще всего подобные искажающие эффекты появляются, когда у исследователя недостаточно наблюдений и поэтому он дополняет изучаемую выборку данными из других родственных совокупностей (данные за разные годы, продукция разных предприятий и т.п.); иными словами, когда выборка данных – неоднородная.

Если для каждого наблюдения известны значения z = x_k , то при изучении корреляции между x = x_i  и y = x_j  появляется возможность предварительно скорректировать все значения переменных x_i  и x_j  на средний уровень показателя x_k , для чего запишем уравнения регрессии между x_i – x_k и x_j – x_k :

;

.

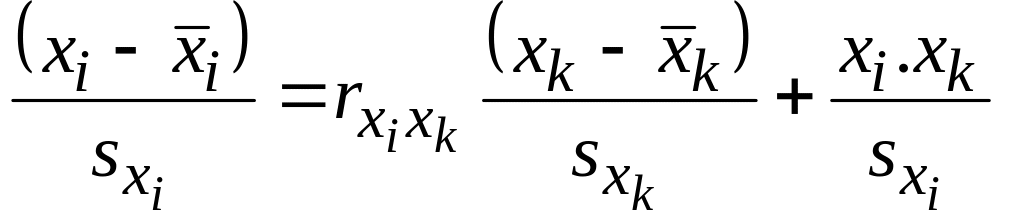Обратите внимание на новые обозначения остатков моделей – они тут обозначены через x_i.x_k и x_j.x_k , чтобы показать, что они не зависят от переменной x_k , изменчивость x_k  учтена в модели, переменная x_k  зафиксирована на среднем уровне.

Определяем "коэффициент частной корреляции" как коэффициент корреляции между остатками моделей, скорректированных на средний уровень x_k :

.

После некоторых преобразований получаем формулу:

.

По аналогии можно записать:

.

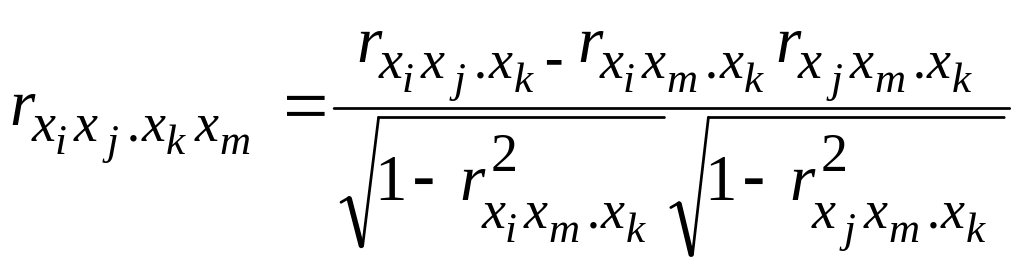Здесь при вычислении коэффициента частной корреляции между x_i  и x_j  фиксируются сразу два показателя x_k  и x_m .

Анализируя числитель и оба подкоренных выражения в формуле коэффициента сачтной корреляции, замечаем, что они получаются как промежуточные результаты при решении системы нормальных уравнений методом Гаусса–Жордана.

Предположим, мы собираемся составить методом последовательного подключения трехфакторную модель: Y = ₁X₁ + ₂X₂ + ₃X₃ . На каждом шаге надо подключать в модель наиболее значимый член и проверять целесообразность дальнейших подключений. На первом шаге значимость пока еще не подключенных членов оценивается обычными коэффициентами корреляции, поэтому в модель первой подключается переменная с максимальным (по модулю) значением коэффициента . Пусть для примера это будет переменная Х₃ . Тогда после первого этапа подключения надо будет вычислить коэффициенты частной корреляции и найти среди них наибольший (по модулю) – это определит выбор следующей переменной, которая будет подключаться на следующем этапе. Ниже изображен первый этап преобразований Гаусса–Жордана в табличной форме.

№	У	Х1	Х2	Х3	Примечания
1	1
2		1
3			1
4				1
5				0
6				0
7				0
8

Система нормальных уравнений в стандартизованной форме записана в строках 2–4 вышеприведенной таблицы. Очень полезно добавить первой строкой коэффициенты корреляции с результативной переменной и производить преобразования Гаусса–Жордана и с этой строкой. На первом этапе подключается Х₃ (разрешающий элемент выделен цветом и рамочкой). В строках 5–6 приведена преобразованная система уравнений после исключения Х₃ (в столбце Примечания указаны выполненные действия). В строке 8 подсчитаны коэффициенты частной корреляци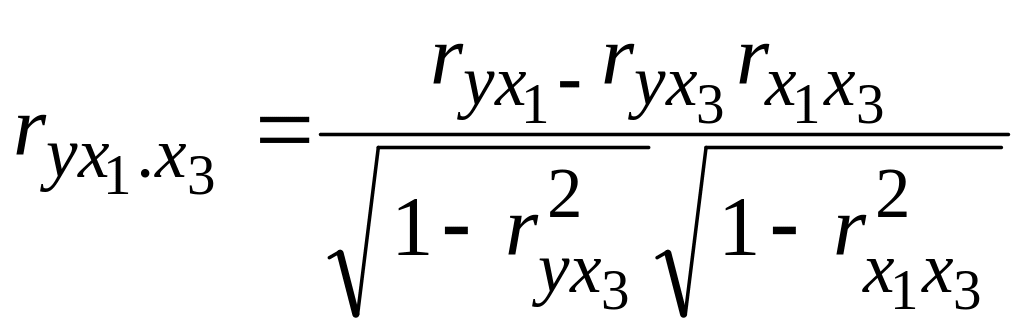и:

и .

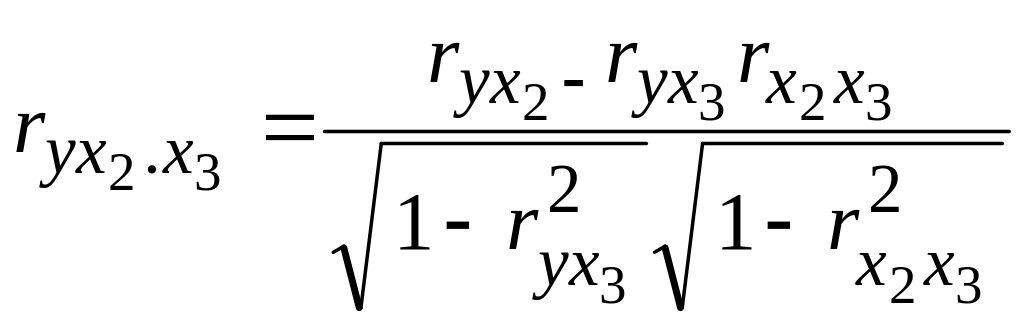Отмечаем, что числители для этих формул уже вычислены в строке 5 (преобразованная строка 1), а подкоренные выравжения расположены в диагональных клетках таблицы.

Следующая переменная выбирается по максимуму абсолютной величины частных коэффициентов корреляции и выполняется очередной этап преобразований Гаусса–Жордана.

В диагональной клетке преобразованной строки 1 автоматически получается число, пропорциональное величине остаточной дисперсии, что дает возможность на каждом шаге проверять целесообразность дальнейшего подключения неизвестных.