Вопросы для самопроверки

1. Какая разница между понятиями "значимость корреляционной связи" и "значимость регрессионной модели"?

2. Что такое "коэффициент детерминации", каковы его свойчтва?

3. Как вычисляется корреляционное отношение? Каковы ее свойства?

4. Как проверяется адекватность регрессионной модели?

5. Чем отличаются расчеты параметров модели по исходным и по сгруппированным данным?

6. Что такое "коэффициент контингенции"?

7. Как вычисляются коэффициенты контингенции Крамера и Кендела?

8. Как проверить значимость коэффициентов контингенции?

9. Что такое "коэффициент ранговой корреляции Спримена"? Как его можно вычислить?

Лекция 16. Линейный регрессионный анализ в стандартизованных переменных

Традиционно все формулы многомерного линейного регрессионного анализа записывают в стандартизованних переменных:

.

В этих переменных многие формулы принимают простейший вид, поэтому сложные вопросы анализа чаще всего обсуждаются именно в стандартизованных переменных.

Стандартизация позволяет выявить некоторые сомнительные значения данных, например, выбросы, которые могут появиться в результате ошибок при переписывании и наборе данных. Кроме описок, опечаток, ошибок измерения, выбросы могут быть следствием принадлежности сомнительных данных до другой совокупности: (например, когда в выборку включают данные о продукции другого предприятия, за другой временной период, когда часть наблюдений измерена другим прибором с другой шкалой калибровки и т.д.). Конечно, такие данные следует удалить из выборки и изучать отдельно. Возможность выявления выбросов основана на правиле 3-х сигм, которое утверждает, что крайне редко встречаются случайные ошибки, превышающие по модулю утроенное стандартное отклонение. Обычно все значения стандартизованных переменных Y, X_i не выходят за пределы интервала , а если встречаются большие отклонения, то такие данные следует выделять и проверять. Чаще всего границы интервала вариации стандартизованных переменных оказываются близкими к .

Сразу же отметим, что несмотря на более простой вид формул регрессионного анализа в стандартизованных переменных, никакого сокращения объема вычислителной работы не будет, т.к. добавляются опрерации нормирования переменных, более сложного составления системы нормальных уравнений и обратного перхода к исходным переменным после завершения вычислений.

Итак, последовательно преобразуем уравнение регрессии

к центрованной и стандартизованной формам:

,

,

,

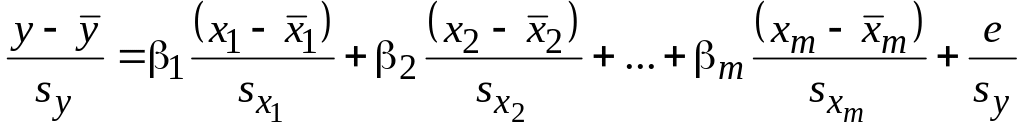где обозначено , , .

Внимание! Обычно коэффициенты регрессии b_j и остатки модели e_i рассматривают как оценки соответствующих генеральных значений _j , _i . Однако теперь обозначния _j , _i  используются как выборочные оценки (только в стандартизованных переменных).

На стадии центрирования уже было использовано одно из уравнений нормальной системы (або ), поэтому в окончательной записи уравнеия регрессии в стандартизованных переменных отсутствует свободный член ₀ = 0.

Составляем остальные уравнения нормальной системы ( )

,

которую приводим к виду:

,

поскольку для стандартизованных переменных , .

Формулу для расчета остаточной дисперсии получаем, преобразовывая выражение

,

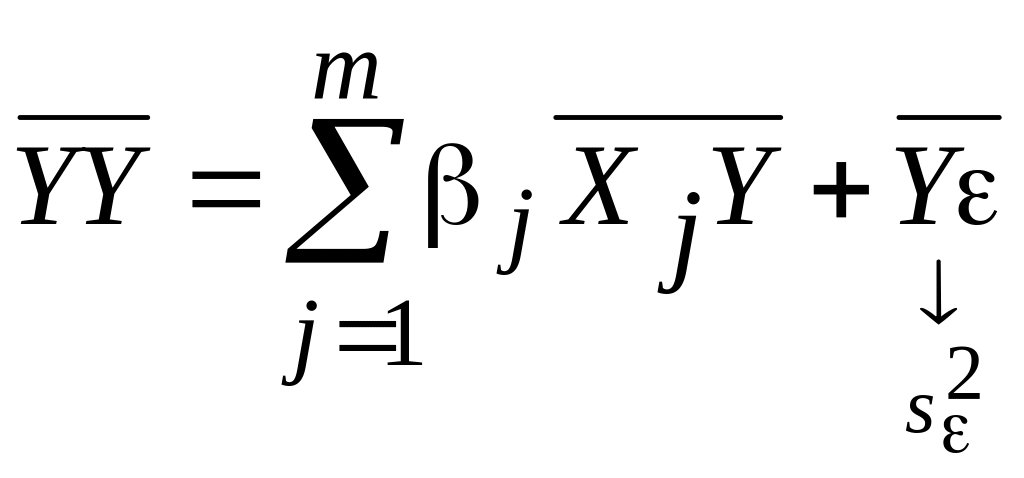где , , :

.

Отсюда получаем очень простую и легко запоминаемую формулу для расчета коэффициента детерминации:

.

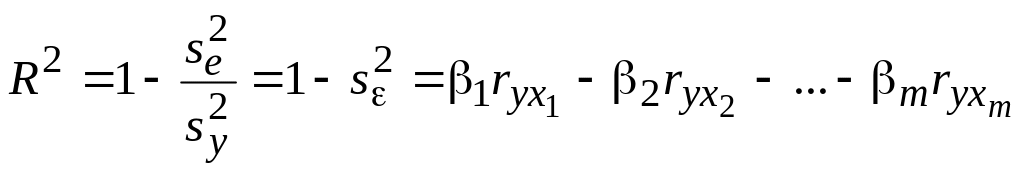После решения системы нормальных уравнений и вычисления коэффициента детерминации делаем обратный переход к исходным переменным, пересчитывая коэффициенты регрессии по формулам:

;

.

Наконец, получаем выражение для расчета несмещенной оценки остаточной дисперсии:

,

где dfe – число степеней свободы остатка модели dfe = n – m – 1.

Значимость модели в целом проверяем с помощью критерия Фишера , который надо сравнивать с табличными значениями F_(m, dfe) .

Если обозначить через c_ij  элементы матрицы, обратной к матрице коэффициентов корреляции , т.е. обратной к матрице системы нормальных уравнений в стандартизованной форме, то можно получить такие формулы для дисперсий и ковариаций стандартизованных -коэффици­ентов:

,

Эти формулы дают возможность оцинить значимость отдельных членов регрессионной модели по критерию Стьюдента

,

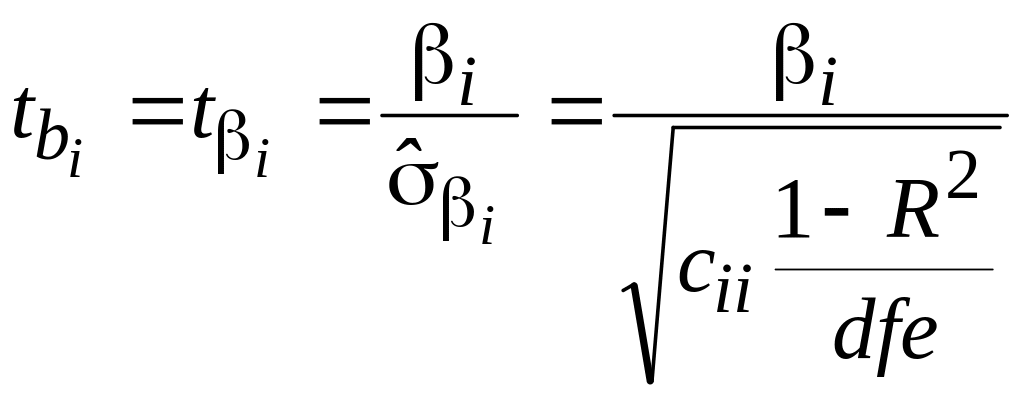построить доверительные интервалы на коэффициенты регрессии ("инструменты экономического воздействия" – по выражению К. Доугерти)

и вычислить дисперсии расчетных значений

.

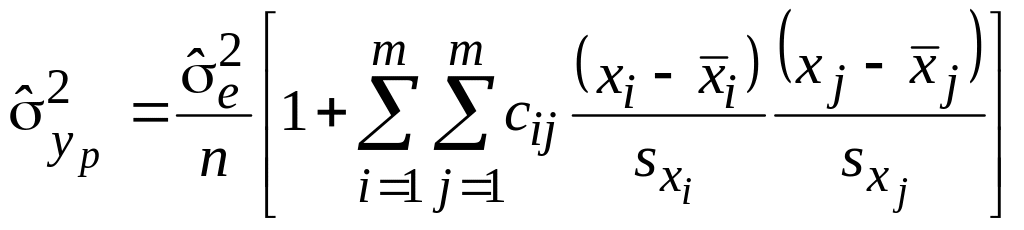Теперь для любого набора значений аргументов можно вычислить y_p вместе с границами его 95%-ного доверительного интервала y_p  y_p , где

.

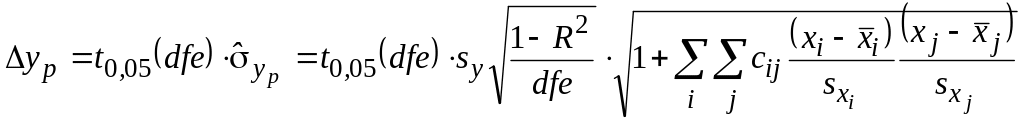Наличие на графиках 95%-й доверительной полосы позволяет установить границы применимости регрессионной модели.

Рассмотрим частный случай однофакторной (m = 1) линейной модели:

y = b₀ + b₁x .

Уравнение регрессии в стандартизованных переменных имеет вид Y = ₁X + , где обозначено , . Система нормальных уравнений для этого частного случая сводится к одному равенству ₁ = r_xy . Коэффициент детерминации R² = ₁r_xy = (r_xy)² здесь равен квадрату коэффи­циента парной корреляции.

Формулы обратного перехода к исходным переменным:

.

Выражение для расчета дисперсии остатка модели принимает вид:

,

где dfe = (n – 2) – число степеней свободы остатка модели при m = 1.

Корреляционная матрица состоит из единственного элемента r_xx = 1, обратная матрица также содержит один эдемент с₁₁ = 1, откуда получаем формулу для расчета дисперсии -коэффициента в виде:

.

Значимость коэффициента регрессии оцениваем по критерию Стьюдента:

,

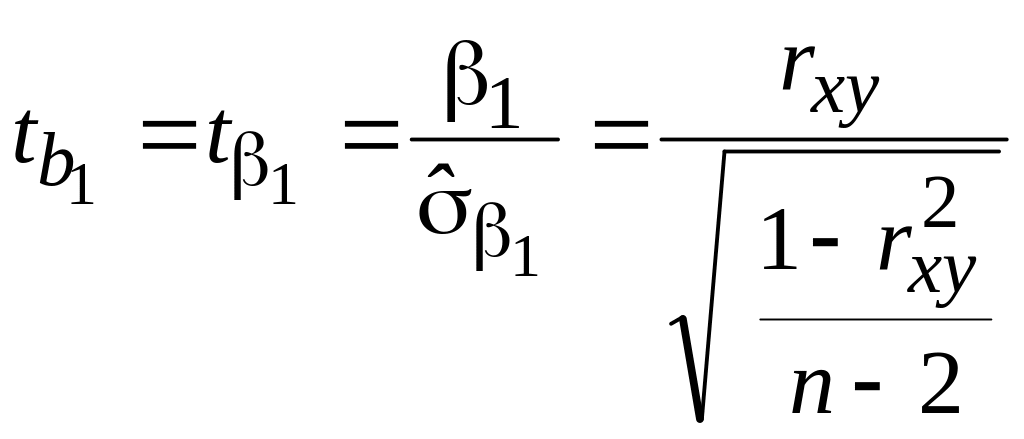а значимость модели в целом по критерию Фишера . Нетрудно убедиться, что для одномерного случая эти два критерия совпадают, т.к. получилось, что (значимость коэффициента регрессии автоматически означает значимость модели).

Пока все вышеприведенные формулы мы уже выводили ранее. Новыми для нас является интервальная оценка коэффициента регрессии

и формула для расчета дисперсий расчетных значений

.

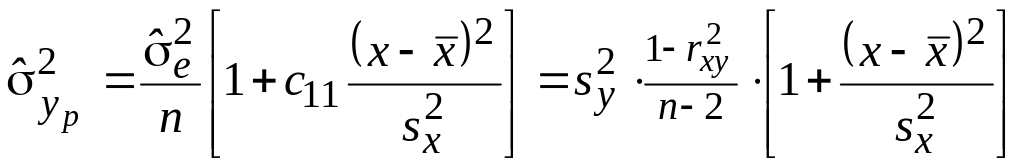Оказывается, что наиболее надежные результаты расчета (с наименьшей случайной ошибкой) будут вблизи центра рассеивания наблюдаемых емпиричных точек (когда ). По мере удаления от центра увеличивается случайная ошибка расчетных значений, что ставит пределы применимости регрессионной модели.

На основе центральной предельной теоремы можно утверждать, что при достаточном объеме выборки любые суммарные характеристики, в частности, , b₁ , y_p(x), будут распределены асимптотически нормально, для этих характеристик известны несмещенные оценки дисперсий, поэтому для них возможно построить 95%-ные доверительные интервалы. Так, для расчетных значений однофакторной линейной модели y_p(x) = b₀ + b₁x довери­тельная ошибка y_p вычисляется по формуле:

,

где для равняется 2.

Доверительный интервал y_p(x)  y_p(x) с гарантией 95% накрывает неизвестное нам математическое ожидание M(y | x). Границы этих интервалов для каждого расчетного значения образуют доверительную полосу вокруг линии регрессии (полосу неопределенности). Любые кривые, графики которых целиком размещаются в полосе неопределенности, представляют собой множество равноправных конкурирующих моделей – опытных данных не достаточно, чтобы сделать обоснованный выбор между ними.

Рассмотрим упрощенный графический способ построения границ доверительной полосы для одномерной регрессии. Выражение для y_p(x) с некоторой заменой обозначений является уравнением сопряженной гипербо­лы , или , где , Y = y_p  – новые переменные; a = s_x , – полуоси гиперболы. График сопряженной гиперболы изображен на рис. 16.1.

О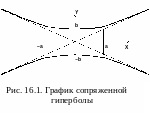 тмечаем следующие особенности этого графика: ширина гиперболичной полосы на интервале [‑а, а] приблизитель­но однакова и равняется ±b; далее границы полосы заметно расширяются, приближа­ясь к линейним асимптотам – продолжениям диагоналей прямоуголь­ника со сторонами (±а, ±b).

В реальных переменных (x, y) самое узкое место полосы сдвинуто вправо на (с учетом знака) и полоса вытянута вдоль линии регрессии. На інтервале ( , ) величина доверительной ошибки практически постоянна и равняется , ( – "ошибка среднего").

Наносим эти границы на график y_p(x) = b₀ + b₁x. Строим параллелограм со сторонами ( , ). В этом параллелограме проводим диагонали и продолжаем их за его границы. Продолжения диагоналей и есть границы 95%-ной доверительной полосы для . Саму сглаживающую гиперболу можно не наносить (если график строится вручную).

Пример. Пусть n = 60; , , s_x = 1,544; s_y = 4,348; r_xy = 0,669;

.

Вычисляем:

.

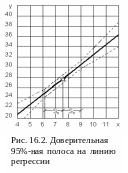
На рис. 16.2 сплошной линией изображен график линии регрессии, звездочкой – центр ( ); от центра вверх и вниз откложено 0,8485 и на интервале построен параллелограм; две стороны параллелограма и продолжения его диагоналей представляют границы доверительной полосы на линию регрессии.

Кроме доверительной полосы на расчетные значения можно еще построить доверительную полосу на разброс данных вокруг линии регрессии (на прогнозные значения результативной пременной). Тут необходимо учесть, что дисперсия прогнозных значений слагается из случайной дисперсии данных и дисперсии расчетных значений , где обозначено .