Коэффициент ранговой корреляции Спирмена

Если X, Y – порядковые переменные, то с ними не допустимы никакие арифметические операции, например, разность двух значений (x_j – x_i) ничего не означает, т.к. из сравнения x_j > x_i следует только, что одно значение больше другого, но неизвестно, на сколько больше. Если переменные ранжированы, то их ранги являются номерами при расположении значений переменной в порядке возрастания какого-то признака. Так, из сравнения рангов x₃ = 3 и x₆ =6 следует, что между элементами x₃ и x₆ есть еще два элемента с рангами x₄ = 4 и x₅ = 5. Если несколько элементов неразличимы по данному признаку, то им всем присваивается средний ранг из их номеров по-порядку. Такие группы переменных называются "связками".

Спирмен вывел формулу для оценки тесноты связи между ранжированными переменными, причем при выводе не использовались никакие сомнительные арифметические операции. Формула эта достаточно простая при отсутствии связок, но усложняется при их наличии.

И тут нам сказочно повезло. Кендел доказал, что коэффициент ранговой корреляции Спирмена численно равен коэффициенту парной корреляции Пирсона, если ранги считать числовыми значениями переменных. Еще раз отметим, что вовсе не утверждается, что с рангами всегда можно поступать, как с обычными числами, но коэффициент корреляции можно расчитывать обычным образом вручную или по готовым программам на компьютере

Вывод формулы для коэффициента ранговой корреляции Спирмена

Пусть p_k , q_k – ранги двух показателей X и Y. Рассмотрим случай отсутствия связок (групп одинаковых рангов).

Наблюдения всегда можно отсортировать в порядке возрастания одной из переменной: p_k = k = 1, 2, 3, … , n. Ранги q_k – те же числа, но в другом порядке. Мерою тесноты связи между показателями X и Y может быть сумма квадратов разностей рангов

.

Если ранги двух показателей совпадают p_k = q_k , то S = 0, и это соответствует наиболее тесной положительной связи. Если порядок следования q_k  противоположен порядку следования p_k , то S = S_max , что соответствует наиболее тесной отрицательной связи. Необходимо найти величину S_max . Для этого случая имеем p_k + q_k = n + 1, p_k = k, q_k = n + 1 – k, p_k – q_k = 2k – (n + 1). Отсюда следует:

S_max = (2k – (n + 1))² = 4k² – 4(n + 1)k + (n + 1)²n.

Поскольку известны формулы для сумм и сумм квадратов последовательных целых чисел и , то окончательно получаем:

Вместо меры S вводим меру связи Спирмена

,

которая равна  = 1 для S = 0 (для наиболее тесной положительной связи), и  = –1 для S = S_max (для наиболее тесной отрицательной связи).

Полученная формула существенно усложняется при наличии связок – групп неразличимых объектов, для которых принимается одинаковые значения рангов, средних для каждой группы.

Пусть t – количество неразличимых объектов в связке для показателя X, а  – коли­чество неразличимых объектов в связке для показателя Y. Вычисляем поправки: , и скорректированный коэффициент ранговой корреляции:

.

Пример. Определим тесноту связи между уровнем механизации работ X и производительностью труда Y по 10-и промышленным предприятиям. Данные ранжированные, в рангах показателя Y имеется одна связка из двух объектов (два предприятия с одинаковой производительностью труда).

k	pk	qk	pk–qk	(pk–qk)2	(pk)2	(qk)2	pkqk
1	1	4	–3	9	1	16	4
2	2	1	1	1	4	1	2
3	3	2	1	1	9	4	6
4	4	3	1	1	16	9	12
5	5	7	–2	4	25	49	35
6	6	5	1	1	36	25	30
7	7	6	1	1	49	36	42
8	8	8,5	–0,5	0,25	64	72,25	68
9	9	8,5	0,5	0,25	81	72,25	76,5
10	10	10	0	0	100	100	100
Суммы	55	55	0	18,5	385	384,5	375,5

Вычисляем коэффициент ранговой корреляции Спирмена без поправки на связку:

.

Вычисляем поправку и скорректированный

коэффициент ранговой корреляции:

Для сравнения вычисляем обычный коэффициент парной корреляции Пирсона. Все необходимые суммы подсчитаны в вышеприведенной таблице.

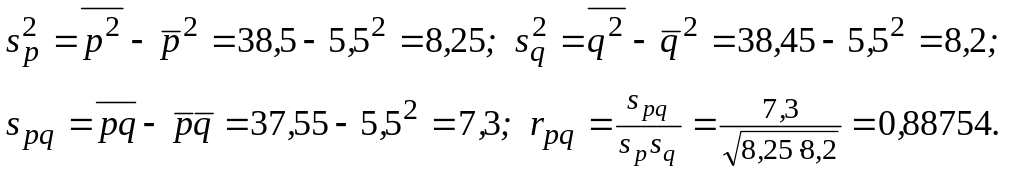
Полученные значения _s и r_pq совпали со всеми десятичными знаками.

Покажем, что коэффициент ранговой корреляции Спирмена абсолютно совпадает с обычным коэффициентом парной корреляции Пирсона, вычисленным по рангам  = r_pq .

Т.к. p_k = k, а q_k – те же числа, но в другом порядке, то будут равны их средние и дисперсии .

Преобразуем выражение S = (p_k – q_k)² :

.

Отсюда:

Итак, формально коэффициент ранговой корреляции Спирмена равняется обычному коэффициенту парной корреляции Пирсона, вычисленному по рангам p_k , q_k.