Проверка адекватности модели

Недаром ошибки модели е называются "остатками модели", т.к. кроме случайных ошибок в них включаются систематические ошибки выбора неверной формы связи (ошибки спецификации модели). Если у нас есть мера чисто случайной изменчивости (дисперсия данных по повторениями опыта), то остатки модели е можно разложить на две компоненты – случайную  и систематическую : е =  + . Точно так же разлагается сумма квадратов отклонений SSe = SS + SS и число степеней свободы dfe = df + df.

Для проверки значимости систематической ошибки  (ошибки неадекватности модели) заполняем таблицу дисперсионного анализа 3.

Таблица дисперсионного анализа 3 для оценки адекватности регрессионной модели

Источник изменчивости	Суммы квадратов	ЧСС	Средние квадраты	Дисперсионное отношение
Неадекватность	SS = (2 – R2)SSy	df = p – 1 – m	MS = SS / df	FА = MS / MS
Случайность	SS = (1 – 2)SSy	df = n – p	MS = SS / df
Остаток модели	SSe = (1 – R2)SSy	dfe = n – 1 – m	MSe = SSe / dfe

Две строки этой таблицы (Остаток модели и Случайность) дублируют соответствующие строки таблиц дисперсионных анализов 1 и 2.

Получено следующее выражение для дисперсионного отношения Фишера

,

которое надо сравнивать с табличными значениями F_0,05(df; df) и F_0,01(df; df). Если окажется, что F_А < F_0,05 , систематической ошибкой можно пренебречь и считать модель адекватной. Но если окажется, что F_А > F_0,01 , то систематической ошибкой пренебречь нельзя, придется искать более подходящую форму связи.

Пример. Ниже в корреляционной таблице приведены результаты двойной группировки данных n = 154 наблюдений; принято р = 7 интервалов равной ширины по переменной Х и q = 6 интервалов равной ширины по переменной Y. При группировках на интервалы равной ширины всегда можно перейти к условным переменным (линейные преобразования переменных) так, чтобы в новых переменных центры интервалов выражались последовательными целыми числами (номерами интервалов). Эти линейные преобразования переменных не изменяют ни последующих выводов анализа, ни вида графиков (у которых будет только другая разметка осей).

Y X	1	2	3	4	5	6	7	l=m	mX	V
6	3	0	0	0	0	0	0	3	3	1
5	2	8	3	0	0	0	0	13	27	2,077
4	2	17	4	3	0	1	0	27	66	2,444
3	0	7	20	13	4	0	0	44	146	3,318
2	0	0	4	12	20	5	4	45	218	4,844
1	0	0	0	5	9	6	2	22	115	5,227
k=m	7	32	31	33	33	12	6	154
mY	36	129	99	80	61	20	10
U	5,143	4,031	3,194	2,424	1,848	1,667	1,667

В последней строке и последнем столбце таблицы вычислены средние групповые U_i и V_j.

Вычисляем параметры линейной модели.

Х_ср = k_iX_i / n = 3,734;   (Х²)_ср = k_i(X_i)² / n = 16,188;   (s_X)² = (Х²)_ср – (Х_ср)² = 2,247;

Y_ср = l_jY_j / n = 2,825;    (Y²)_ср = l_j(Y_j)² / n = 9,500;     (s_Y)² = (Y²)_ср – (Y_ср)² = 1,521;

(XY)_cp = m_ijX_iY_j / n = 9,130;    s_XY = (XY)_cp – Х_срY_ср = –1,417;

r_XY = s_XY / (s_Xs_Y) = –0,766;       (r_XY)² = 0,587.

b₁ = r_XY(s_Y / s_X) = –0,630;      b₀ = Y_ср – b₁Х_ср = 5,179.

Линейной моделью Y_p = 5,179 – 0,630X объясняется 58,7% общей изменчивости данных. Эта модель значима, т.к. дисперсионное отношение превышает табличное значение F_0,01(1; 152) = 6,80.

Вычисляем индексы детерминации.

p = 7;   U_cp = Y_cp = 2,825;   (U²)_cp = k_i(U_i)² / n = 8,948;   (s_U)² = (U²)_ср – (U_ср)² = 0,969;

q = 6;   V_cp = X_cp = 3,734;    (V²)_cp = l_j(V_j)² / n = 15,338;    (s_V)² = (V²)_ср – (V_ср)² = 1,397;

;    .

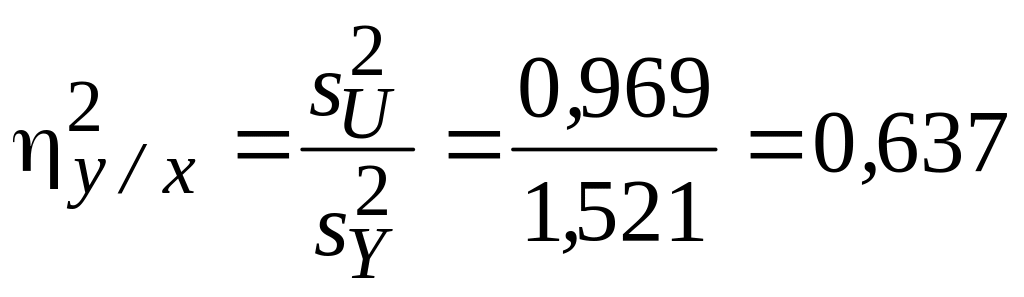Корреляционной зависимостью у / х объясняется 63,7% общей изменчи­вости данных (сопряженной зависимостью х / у объясняется 62,2%). Корреляционная зависимость значима, т.к. дисперсионное отношение превышает табличное значение F_0,01(6; 147) = 2,93.

Проверяем адекватность линейной модели. Вычисляем дисперсионное отношение и сравниваем его с табличными значениями F_0,05(5; 147) = 2,28 и F_0,01(5; 147) = 3,14. Т.к. вычисленное значение F_A = 4,06 > F_0,01 , систематической ошибкой пренебречь нельзя, линейная модель – неадекватная, требуется найти более подходящую нелинейную форму связи.

На рис. 15.1 (а) изображены графики эмпирической и линейной регрессии, откуда видно, действительная зависимость – нелинейная, узлы эмпирической линии регрессии закономерно уклоняются от графика линейной регрессии.

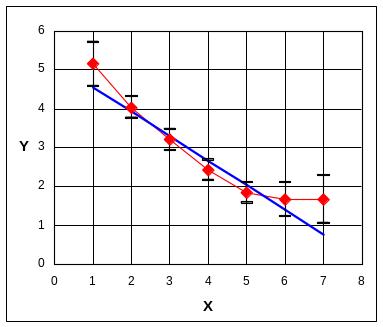
а б

Рис. 15.1. Соответствие между эмпирической и теоретическими линиями регрессии

а – линейная модель Y_p = 5,179 – 0,630X; б – нелинейная модель

Для каждого узла (среднего группового) построены 95%-ные довери­тельные интервалы шириною НСР_0,05 , где . Крайние узлы на рис. 15.1 (а) существенно уклоняются от линейной регрес­сии, ее график не пересекает крайних доверительных интервалов.

На рис. 15.1 (б) построен график нелинейной зависимости , который пересекает доверительные интервалы для всех узлов эмпирической линии регрессии. Коэффициент детерминации возрос до R² = 0,611; диспер­сионное отношение F_A = 2,12  понизилось и стало уже меньше табличного F_A < F_0,05 . Найденная нелинейная модель – адекватная.

Таблицы сопряженности и коэффициенты контингенции

Если обе переменные – качественные, измеренные в наиболее общей шкале имен, то таблицу частот m_ij совместного появления категорий (X_i , Y_j) разных переменных называют "таблицей сопряженности". В этой таблице X_i и Y_j – имена категорий (не числа), поэтому никакие арифметические операции с ними невозможны. Как и для корреляционной таблицы, подсчитывается общая сумма частот n , а также суммы частот по столбцам k_i и строкам l_j таблицы.

Относительные частоты есть оценки вероятностей появления категорий X_i и Y_j . Проверяется гипотеза о независимости качественных переменных X, Y (нуль-гипотеза). Имеется возможность определить теоретические частоты совместного появления любой комбинации категорий (X_i , Y_j), которые ожидаются при справедливости нуль-гипотезы. Действительно, при взаимной независимости категорий (X_i , Y_j) вероятность совместного появления такой комбинации равна произведению их вероятностей , откуда получаем ожидаемые частоты в виде .

Наблюдаемые и ожидаемые частоты сравниваем по критерию Пирсона:

.

Табличные значения находим для ЧСС = (р – 1)(q – 1), где р,  q – число категорий для X, Y.

Если окажется, что , нуль-гипотеза отклоняется, и делается вывод о том, что переменные X, Y связаны между собой. Тогда появляется проблема оценки тесноты этой связи. Предложено несколько мер тесноты связи между качественными переменными, из которых мы рассмотрим две – "коэффициент контингенции" Крамера , и "коэффициент контин­генции" Кендела . При абсолютном совпадении наблюдаемых и ожидаемых частот статистика Пирсона ² равна нулю и равны нулю оба коэффициента контингенции.

	X1	X2	X3	X4	lj
Y1	m11	m12			m11+m12
Y2			m22		m22
Y3				m33	m33
ki	m11	m12	m22	m33	n

Максимальное значение получается при наиболее тесной связи, когда каждой категории одной переменной соответствует только одна категория другой переменной (функциональное соответствие). Т.к. категории можно переставлять, при наиболее тесной связи таблица сопряженности приобретает блочно-диагональный вид. Пусть p > q (например, р = 4, q = 3). Вычисляем для этого случая статистику Пирсона:

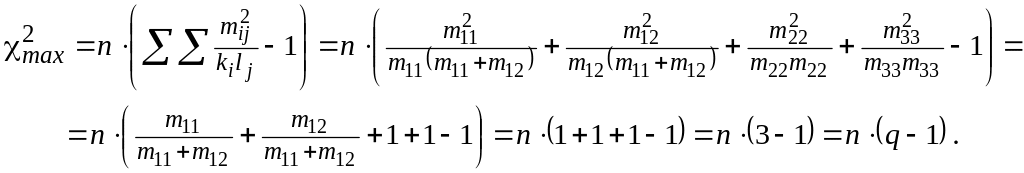
Таким образом, коэффициент контингенции Крамера можно записать в виде: , где d = min{p, q}. Коэффициент контингенции Кендела изменяется от 0 до . Скорректируем его: .

Как правило, оказывается, что С  К КК.

Пример. Рассмотрим предыдущую корреляционную таблицу, размером 7  6 с числом наблюдений n = 154 и будем считать значения переменных X, Y именами различных категорий. Суммы частот по столбцам и строкам таблицы уже найдены. Ниже в таблице такого же размера подсчитаны отношения :

Y X	X1	X2	X3	X4	X5	X6	X7
Y6	0,429	0	0	0	0	0	0
Y5	0,044	0,154	0,022	0	0	0	0
Y4	0,021	0,334	0,019	0,010	0	0,003	0
Y3	0	0,035	0,293	0,116	0,011	0	0
Y2	0	0	0,011	0,097	0,269	0,046	0,059
Y1	0	0	0	0,034	0,112	0,136	0,030

Вычисляем их сумму (2,29) и статистику Пирсона ² = 154(2,29 – 1) = 198,7, которую сравниваем с табличным значением . Т.к. , делаем вывод о существовании значимой связи между X и Y.

Коэффициенты контингенции Крамера, Кендала и скорректированный коэффициент КК равны соответственно , , . Сравним эти меры с коэффициентом корреляции | r_XY | = 0,766 и с корреляционным отношением .

Соответсвие между скорректированным коэффициентом контингенции Кендела и корреляционным отношением – самой объективной мерой тесноты корреляционной связи между количественными переменными – очень хорошее (КК   ).