Однофакторная линейная зависимость

Для этого частного случая можно получить готовые формулы для МНК-оценок параметров модели и коэффициента корреляции.

Систему нормальных уравнений для линейной модели

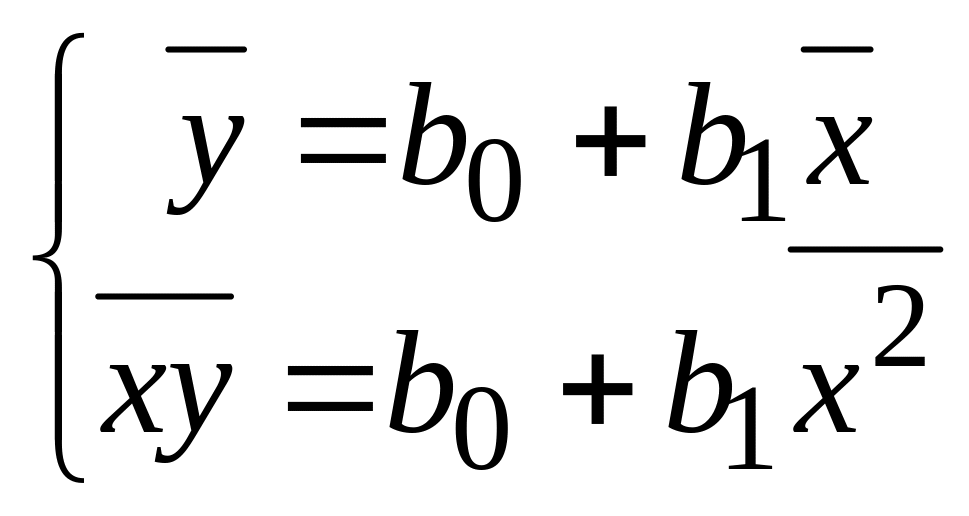
можно решить в общем виде и получить формулы для расчета "коэффициента регрессии" и свободного члена .

Из формулы для дисперсии остатка модели

получаем коэффициент детерминации в виде: .

Извлекаем корень квадратный из коэффициента детерминации и получаем "коэффициент парной корреляции" (Пирсона): .

Таким образом, коэффициент множественной кореляции для случая однофакторной линейной зависимости совпадает (по модулю) с коэффициентом парной кореляции R = | r_xy |. В общем же случае он совпадает с коэффициентом парної кореляції между расчетными и наблюдаемыми значениями .

Коэффициент парной корреляции r_xy и его квадрат (коэффициент детерминации R² оценивает тесноту линейной связи. Если r_xy = 0, линейной связи нет; при r_xy = 1 имеем точную линейную зависимость. На рис. 14.5 изображены возможные ситуации при разных значениях r_xy .

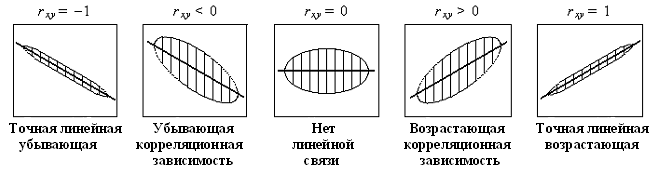
Рис. 14.5. Различные случаи тесноты связи

С использованием коэффициента парной корреляции можно записать несколько в иной форме ранее найденные формулы:

;

.

Уравнение регресии удобно записать в стандартизованных переменных

.

Если изменить направление причинно-следственных связей, то получим очень похожее уравнение "сопряженной" регресии:

.

Если же оба показателя (x и y) являются следствиями одной и той же общей причины, то наилучшим описанием связи будет "диагональная регрессия" (Фриша):

,

где знак  соответствует знаку ковариации s_xy или знаку коэффициента корреляции r_xy .

Нелинейные двухпараметрические модели

Как уже было сказано выше, для успешного применения МНК желательно, чтобы форма связи была линейной относительно параметров модели. Для двухпараметричных зависимостей, которые линейно зависят от параметров, или могут быть приведенными к такой форме функциональными преобразованиями, существует графический способ проверки их пригодности для описания данных (иными словами, существует графический способ проверки адекватности модели).

Пусть Y = F(x, y) и X = Ф(x, y) – такие функциональные преобразова­ния, после которых форма связи формально приводится к линейному виду:

Y = a + bX.

Графиком линейной зависимости является прямая, а прямую человек уверенно выделяет среди множества других кривых. Отсюда следует такое правило – если в преобразованных координатах эмпирические точки не группируются вокруг какой-либо прямой, принятая форма связи не является адекватной. С использованием современной вычислительной техники любые графики легко строятся и преобразуются, поэтому описанный способ идентификации формы связи является достаточно эффективным.

Чаще всего используется или логарифмирование, или переход к обратным величинам. На рис. 14.6 приведены справочные сведения о нелинейных двухпараметрических зависимостях, которые могут быть сведены к линейным указанными функциональными преобразованиями. Для наглядности на рис. 14.6 в клетках таблицы приведены эскизы графиков типовых зависимостей.

Ни одна из двухпараметрических зависимостей, приведенных на рис. 14.6, не допускает существования оптимума (максимума или минимума). Если по смыслу задачи ожидается наличие экстремума (оптимума), то следует применять трехпараметрические формы связи, например, квадратичную модель. Квадратичная модель с функциональными преобразованиями переменных способна описывать довольно широкий класс зависимостей с экстремумами.

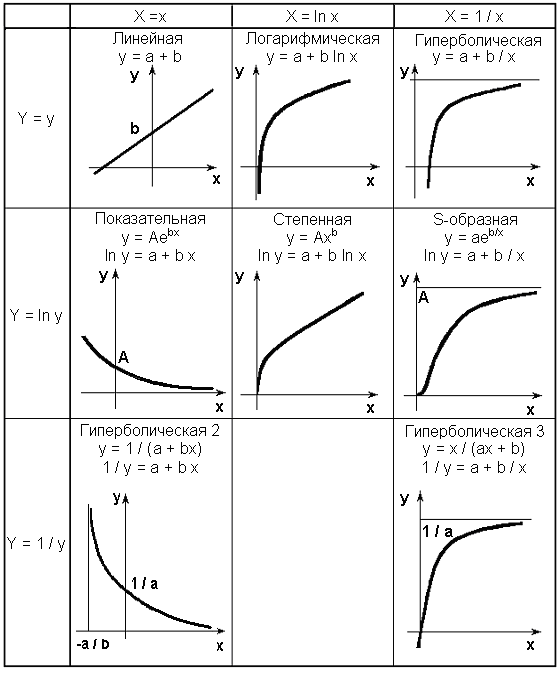
Рис. 14.6. Двухпараметрические зависимости Y = a + bX