Метод наименьших квадратов (мнк)

Данные обычно имеют вид таблицы значений показателей (х₁ , х₂ , у), один из которых является результативным (у) и выражается через оставшиеся переменные (х₁ , х₂), которые иногда называются "факторами".

Предполагается, что форма связи нам известна с точностью до параметров, наилучшие значения которых надо найти по опытным данным (т.е. найти "МНК-оценки параметров"). Для применения метода наименьших квадратов крайне желательно, чтобы параметры входили в форму связи линейным образом, например, так:

– линейная двухфакторная зависимость:        у = b₀ + b₁ x₁ + b₂ x₂ + e;

– квадратичная однофакторная зависимость: у = b₀ + b₁ x + b₂ x² + e;

– нелинейная двухфакторная зависимость: lnу = b₀ + b₁ lnx₁ + b₂ lnx₂ + e.

Здесь b₀ , b₁ , b₂ – параметры модели, которые подлежат определению;

е – ошибки (остатки модели).

Далее будем рассматривать базовую линейную зависимость, к которой могут быть сведены многие другие зависимости соответствующими заменами переменных: у = у_р + е, где у_р = (b₀ + b₁ x₁ + b₂ x₂) 

Условимся суммирование по всем наблюдениям обозначать квадратны­ми скобками (обозначения Гаусса): ; .

По методу наименьших квадратов (МНК) параметры модели b₀ , b₁ , b₂  следует определять из условия минимума суммы квадратов ошибок по всем наблюдениям [e²]  min.

Согласно необходимым условиям экстремума, приравниваем нулю частные производные суммы квадратов ошибок по каждому параметру модели b₀ , b₁ , b₂ . В результате получим такую систему "нормальных" уравнений:

[e] = 0; [ex₁] = 0; [ex₂] = 0.

При преобразованиях были использованы правила:

.

Название система "нормальных" уравнений объясняется терминологи­ей векторного исчисления. Значения любых переменных представляют собой - мерные векторы: y = (y₁ , y₂ , … , y_n); x₀ = (1, 1, … , 1); x_j = (x_j1 , x_j2 , … x_jn); e = (e₁ , e₂ , … , e_n). Два вектора перпендикулярны (ортогональны, нормальны), если их скалярное произведение (сумма значений одноименных компонент) равно нулю . Таким образом, система нормальных уравнений действительное представляет собой запись условий ортогональности (нормальности) вектора ошибок (е) к каждому члену модели (1, х₁ , х₂).

Помножим равенство у = а₀х₀ + а₁х₁ + а₂х₂ + е (где х₀ = 1) на каждую переменную, которые входят в это равенство и вычислим средние полученных выражений по всем наблюдениям. При этом учтем требование нормальности (ортогональности) ошибок к каждому члену модели Получим:

Первые три равенства (объединенные фигурной скобкой) представляют собой систему нормальных уравнений в развернутой форме, а из последних двух равенств получаем выражение для оценки дисперсии остатка модели . Аналогичную формулу имеем для расчета суммы квадратов ошибок: [e²] = [y²] – b₀ [y] – b₁ [yx₁] – b₂ [yx₂]. Таким образом, мы выразили сумму квадратов ошибок через уже найденные суммы. Эта формула понадобится в дальнейшем.

Пример расчета мнк-оценок параметров

Расчеты по методу наименьших квадратов продемонстрируем на оценке параметров квадратичной модели у = b₀ + b₁ x + b₂ x² + e, которая формально сводится к предыдущей двухфакторной линейной модели заменой переменных х₁ = х, х₂ = х² . При этом выясняется, что аргументы х₁ , х₂ не являются "независимыми" переменными в общепринятом понимании, они могут быть связаны между собой, лишь бы определитель системы нормальных уравнений был отличен от нуля. Кроме того, оказывается, что одной объясняющей переменной в нелинейной модели может соответствовать не один, а сразу несколько членов, необходимых для описания нелинейностей.

О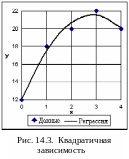 бычно форму связи выбирают по виду расположения эмпирических точек на графике. Например, данные на рис. 14.3 (эмпирические точки) явно уклоняются от прямой, видно наличие оптимума (максимума зависимости); поэтому сочтено, что квадратичная модель у = b₀ + b₁ x + b₂ x² + e будет более адекватно описывать эту нелинейную зависимость.

Условия ортогональности ошибок к каждому члену квадратичной модели приводят к следующей системе нормальных уравнений:

.

Все необходимые суммы подсчитаны в следующей таблице:

	Данные		Расчет сумм
№	x	у	х2	х3	х4	ух	ух2	у2	ур	e
1	0	12	0	0	0	0	0	144	12,114	-0,114
2	1	18	1	1	1	18	18	324	17,547	0,457
3	2	20	4	8	16	40	80	400	20,696	-0,686
4	3	22	9	27	81	66	198	484	21,543	0,457
5	4	20	16	64	256	80	320	400	20,114	-0,114
Суммы	10	92	30	100	354	204	616	1752		0

Вычисленные суммы подставляем в систему нормальных уравнений

и находим ее решение: b₀ = 12,114; b₁ = 6,571; b₂ = –1,143.

Рачетные значения y_p = 12,114 + 6,571x – 1,143x² приведены в той же таблице вместе с ошибками е = у – у_р . График найденной квадратичной зависимости изображен на рис. 14.3, при этом наблюдается хорошее сглаживание исходных данних.

Убеждаемся, что сумма всех ошибок равняется нулю: [e] = 0.

Данных немного, поэтому подсчитаем сумму квадратов ошибок непосредственно: [e²] = (–0,114)² + (0,457)² + (–0,686)² + (0,457)² + (–0,114)² = 0,914.

Для проверки вычислим эту же сумму квадратов по формуле:

[e²] = [y²] – b₀ [y] – b₁ [yx₁] – b₂ [yx₂] = =1752 ‑ 12,11492 ‑ 6,571204 + 1,143616 = 1,116.

Расхождение в результатах расчета двумя способами объясняется погрешностями в вычислении параметров модели с 3-мя десятичными знаками. Если вычислить эти параметры с 4-мя десятичными знаками, то для суммы квадратов ошибок получим значение [e²] = 0,945, а с 5-ю знаками – уже [e²] = 0,915.