Дополнение к выводу формул Краскала–Уоллиса

Математика – это не поваренная книга рецептов, где надо все запоминать без каких-либо доказательств. Конечно, для не математиков сложные выводы можно не приводить, а ограничиться ссылками на соответствующине источники. Но если математические преобразования посильны и поучительны, может стоит их привести как дополнительные (необязательные) материалы к изучению данной темы. Разве не интересно узнать, каким образом была выведена формула для дисперсии средних рангов?

Итак, ранги u_i – это последовательные номера от 1 до n, переставленные в каком-то другом порядке. Поэтому можно найти сумму рангов , сумму квадратов рангов (эту формулу можно найти в справочниках) и сумму произведений рангов .

Сумму рангов в случайной выборке можно представить в виде , где _i = 1, если элемент u_i попал в выборку, и _i = 0, если не попал. Вероятность того, что элемент попадает в выборку, равна , два элемента попадают в одну выборку с вероятностью (выборка без возвращения).

Вычисляем математические ожидания , , . Отсюда получаем дисперсию и ковариацию .

Теперь вычислим математическое ожидание суммы рангов и среднего ранга v = z / k в случайной выборке:

; .

Этот результат мы установили ранее простейшими рассуждениями.

Вычислим дисперсию суммы рангов в случайной выборке:

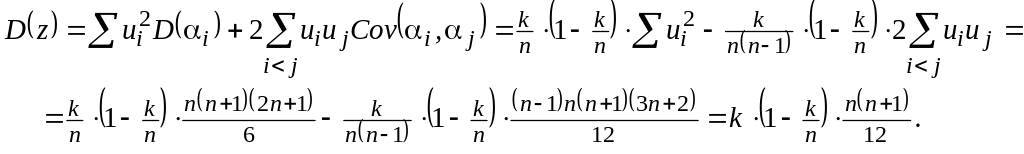
Искомая дисперсия среднего ранга v = z / k в случайной выборке будет в k²  раз меньше: , что и требовалось доказать.:

Вопросы для самопроверки

1. Сформулируйте задачу дисперсионного анализа.

2. Что такое "суммы квадратов"? Напишите разложение общей суммы квадратов на компоненты.

3. Что такое "число степеней свободы"? Напишите разложение общего числа степеней свободы на компоненты.

4. Что такое "средние квадраты"?

5. Что означает дисперсионное отношение Фишера?

6. Как определяется значимость различий между группами наблюдений?

7. Как оценить тесноту связи между классификационной и результативной переменными?

8. Как уточнить, между какими именно группами имеются значимые различия?

9. Что такое "ранги"?

10. Какими преимущества имеет ранговый дисперсионный анализ?

Лекция 14. Регрессионный анализ

Регрессионный анализ предназначен для изучения корреляционных связей между количественными переменными, причем результативная переменная должна быть измерена в количественной непрерывной шкале. Несколько странное название "регрессионный анализ" (почему "регресс", а не "прогресс"?) закрепилось исторически. Дело в том, что характерной особенностью прогресивно возрастающих зависимостей является увеличение темпа возрастания результативной переменной у / х при увеличении абсолютного уровня объясняющей переменной х. Такими зависимостями обычно описываются нестабильные процессы типа взрыва (цепная реакция, демографический взрыв, удвоение числа публикаций через определенный период т.п.). Большинство же интересующих нас биометрических ("био" – жизнь) зависимостей регрессивны, для них характерно насыщение – постепенное снижение эффективности управляющих воздействий (объясняющих переменных), с возрастанием их абсолютных значений темпы прироста результативной переменной снижаются (рис. 14.1).

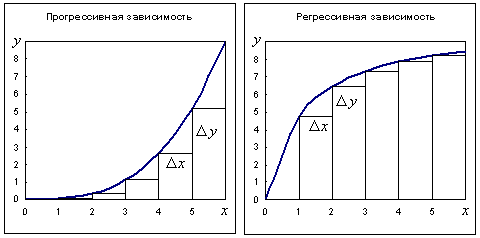
Рис. 13.1 Прогрессивная и регрессивная зависимости

В регрессионном анализе (так же как и в дисперсионном анализе) изучается поведение только одной характеристики распределения результативной переменной – центра группировки Y при каждом значении объясняющих переменных х₁ , х₂ , х₃ и т.д. Следовательно, в регрессионном анализе изучаются корреляционные зависимости. По традиции уравнения этих зависимостей называются "уравнениями регрессии" а их графики – "линиями регрессии". Корреляционно-регрессионный анализ не решает вопроса о направлениии причинно-следственных связей; специалист должен сам указать, какую именно переменную надо считать результативной (остальные переменные тогда будут считаться объясняющими). В регрессионном анализе все ошибки будут отнесены только к результативной переменной, а объясняющие переменные будут считаться неслучайными, измеренными точно. Из-за этой особенности одним и тем же данным будет соответсвовать не одно а несколько, так называемых, "сопряженных" уравнений регресии в зависимости от того, какая именно переменная объявлена результативной. На рис. 14.2 изображены линии "сопряженных" регрессий для двух случайных величин (X, Y), причем на рис. 14.2 (a) за результативную переменную принята переменная Y и найдены ее средние значения М( y | x ) для каждого значения х, а на рис. 14.2 (б) за результатив­ную переменную принята переменная Х и найдены ее средние значения М( х | у ) для каждого значения y.

а б

Рис. 14.2. Сопряженные линии регресии и "диагональная регрессия"

Данный пример соответствует случаю совместного нормального распределения двух случайных величин (X, Y). С уровнем доверия Р = 0,95 практически все точки (95%) попадают в эллиптическую область, поскольку для двумерного нормального закона область рассеивания точек (x_i , y_i) имеет такую форму. Если X – причина, а Y – следствие (рис. 14.2. а), то линия регрессии М( y | x ) = f₁(x) будет совпадать с диаметром эллипса, сопряженным семейству вертикальных хорд (серединами вертикальных хорд эллипса). Если Y – причина, а X – следствие (рис. 14.2. б), то линия регрессии М( х | у ) = f₂(у) будет совпадать с диаметром эллипса, сопряженным семейству горизонтальных хорд (серединами горизонтальных хорд эллипса). Это совсем разные диаметры. Обе сопряженные линии регрессии не совпадают с главной осью эллипса рассеивания – это следствие выбора только одной переменной в качестве случайной (результативной) – величины, которой приписываются все ошибки (случайные и неслучайные). Чаще всего специалист не сомневается в правильности выбора направления причинно-следственных связей. Тогда разумным выглядит предположение, что одна из переменных определяет другую. Однако бывает, что обе переменные (X, Y) являются разными следствиями одной и той же общей причины, что и порождает наблюдаемую связь между ними (например, обе переменные возрастают со временем). В такой задаче нет оснований принимать какую-либо переменную в качестве результативной и считать, что одна переменныя определяет другую; наилучший график зависимости между равноправными переменными X, Y должен совпадать с главной осью рассеивания данных. По традиции этот особый вид зависимости называется "диагональной регрессией". Сразу же отметим, что "диагональная регрессия" не есть "регрессия" (корреляционная зависимость) по определению, т.к. точки диагонали эллипса не являются средними значениями одной из переменных при заданных значениях остальных.