Сравнение двух дисперсий

Английский статистик Р. Фишер изучил распределение отношения несмещенных оценок дисперсии для двух выборок, взятых из одной и той же нормально распределенной совокупности:

,

где в числителе стоит наибольшая из двух оценок дисперсий, а в знаменателе – наименьшая оценка. Распределение Фишера зависит только от чисел степеней свободы числителя и знаменателя F(df₁ , df₂). Внешне график дифференциальной функции распределения Фишера похож на аналогичный график распределения Пирсона. Составлены таблицы с двумя входами (df₁ , df₂) для определения критических значений F_0,05  и F_0,01  (определяется только верхняя граница).

Если вычисленное значение F не превосходит нижней границы F  F_0,05 , нуль-гипотеза о равенстве дисперсий не может быть отвергнута. Нуль-гипотеза отвергается, если вычисленное значение F превосходит верхнюю границу F > F_0,01 . Остальные значения F попадают в область неопределенности критерия.

Для предыдущего примера (4 группы) сравним все 6 пар дисперсий. В нижеследующей таблице для каждой пары выборок выписаны их объемы n_k  и несмещенные оценки дисперсий . Вычислены отношения F большей оценки к меньшей и по таблицам для заданной пары чисел степеней свободы числителя и знаменателя найдены критические значения F_0,05 и F_0,01 .

Группы i – j	ni	nj			F	F0,05	F0,01
1 – 2	103	3	31,004	67,704	2,184	3,09	4,82
1 – 3	103	30	31,004	24,566	1,262	1,71	2,15
1 – 4	103	17	31,004	8,253	3,757	2,07	2,86
2 – 3	3	30	67,704	24,566	2,756	3,33	5,42
2 – 4	3	17	67,704	8,253	8,204	3,63	6,23
3 – 4	30	17	24,566	8,253	2,977	2,20	3,10

Значимые дисперсионные отношения, для которых F > F_0,01 , выделены в таблице, откуда видно, что изменчивость данных в 4-й группе значимо отличается от изменчивости в других группах. При сравнеии 3-й и 4-й групп дисперсионное отношение F = 2,977 попало в область неопределенности критерия Фишера.

Если при оценке значимости разности средних по критерию Стьюдента оказалось, что нельзя пользоваться объединенной оценкой дисперсии, дисперсию разности вычисляют по другой формуле: . Однако при этом возникают проблемы определения соответствующего числа степеней свободы df_ . Согласно методике Уэлча, ЧСС надо определять так:

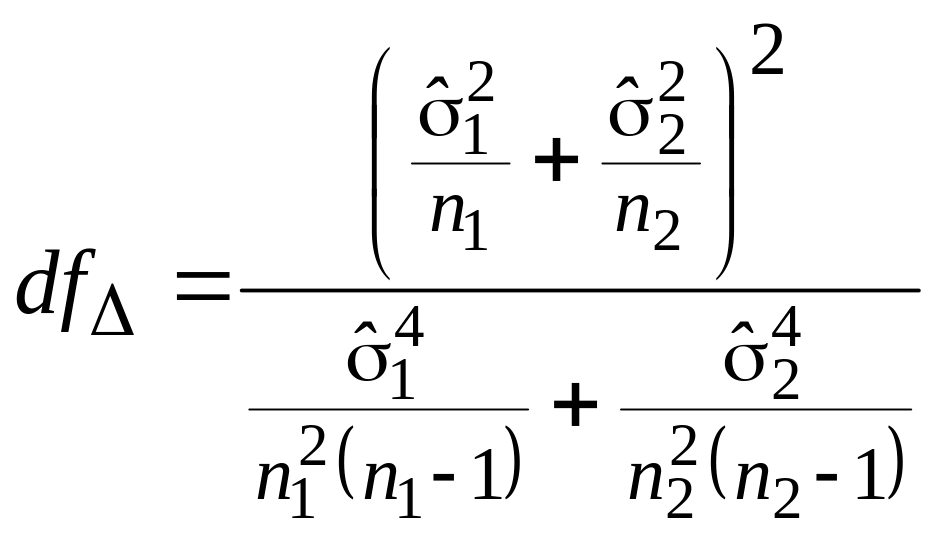
Например, для спорного случая при сравнении 3-й и 4-й групп имеем:

; .

.

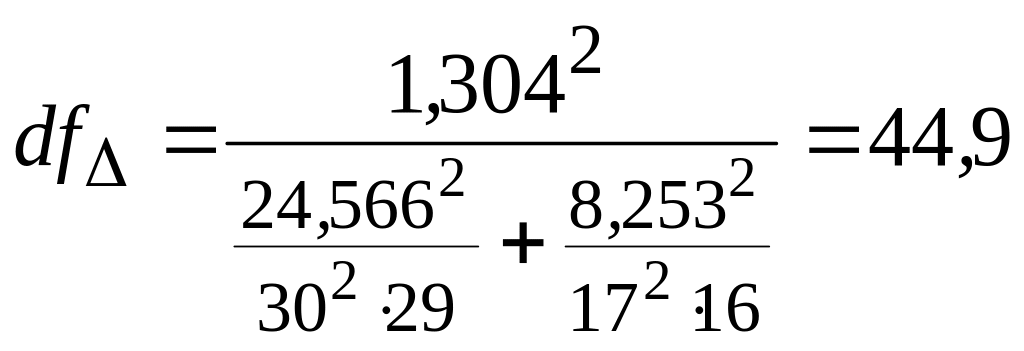Все-равно получилась обычная сумма ЧСС: df_ = (n₃ + n₄ – 2) = 45.

; t_0,05(44) = 2,01; t_0,01(44) = 2,69.

Вычисленное t_ попало в область неопределенности критерия. Ранее (при объединении дисперсий) был сделан вывод об отсутствии значимых различий между выборками 3 и 4.