Проверка гипотезы о равенстве центров двух совокупностей

Пусть две совокупности представлены выборками с характеристиками:

Характеристики	Выборка 1	Выборка 2
Объемы выборок	n1	n2
Средние
Оценки дисперсий
Несмещенные оценки
Суммы квадратов

Оценки дисперсий могут быть обычными или несмещенными ; для любого вида оценок дисперсии вычисляются суммы квадратов отклонений по формулам или .

Совокупности предполагаются независимыми с примерно одинаковой изменчивостью, иными словами, считается, что совокупности могут различаться только центрами (математическими ожиданиями а₁ , а₂).

Последнее предположение о равенстве дисперсий совокупностей можно проверить по критерию Фишера, который будет рассмотрен позже.

Для малых выборок оценки дисперсий могут оказаться малонадеж­ными, поэтому вычисляем объединенную дисперсию: . Число степеней свободы для объединенной дисперсии равно (n₁ + n₂ – 2), т.к. на отклонения наложено 2 связи – сумма первых n₁ отклонений равна нулю и сумма следующих n₂ отклонений также равна нулю (центральное свойство средних).

Согласно центральной предельной теореме, выборочные средние распределены асимптотически нормально: .

Разность выборочных средних также распределена нормально (композиция нормальных законов приводит к нормальному распределению) c характеристиками M() = a₁ – a₂ , , т.к. дисперсия суммы (и разности) независимых случайных величин равна сумме дисперсий.

В таком случае статистика

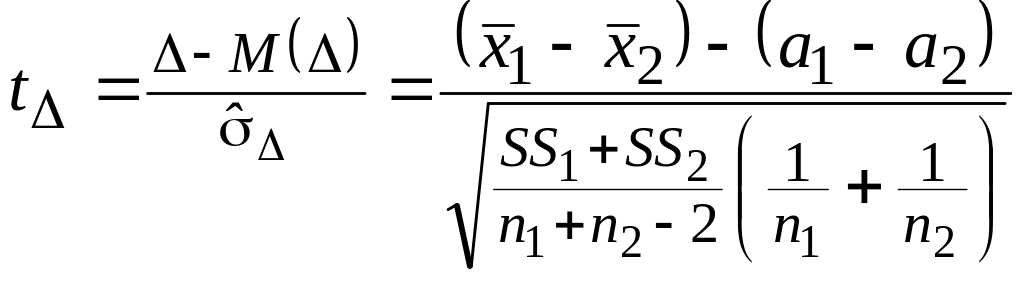
имеет t – распределение Стьюдента с числом степеней свободы df = (n₁ + n₂ – 2).

Нуль-гипотеза заключается в предположении а₁ = а₂ .

Если окажется, что 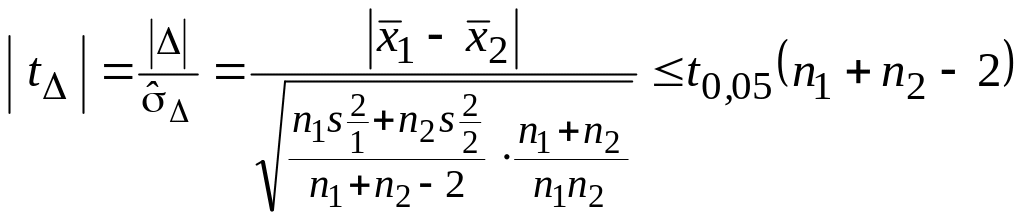, нуль-гипотеза не может быть отвергнута и с уровнем доверия Р = 0,95 принимаем гипотезу о равенстве центров совокупностей. Нуль-гипотеза отвергается при | t_ |  t_0,01 . Остальные значения t_0,05 < t_ < t_0,01 .падают в область неопределен­ности критерия.

Для примера сравним средние 4-х выборок, характеристики которых приведены в таблице:

Выборки	Объемы nk	Средние	Несмещенные оценки	Суммы квадратов
1	103	32,368	31,004	3162,4
2	3	27,367	67,704	135,4
3	30	22,243	24,566	712,4
4	17	19,247	8,253	132,0

Для анализа k групп понадобится сравнить пар; в данном случае получается 6 пар, для которых ниже вычислены ЧСС df_ij , разности , несмещенные оценки дисперсий этих разностей , статистики Стьюдента t_ , и табличные значения t_0,05(df), t_0,01(df):

Группы i – j	ni	nj	dfij	ij		t	t0,05	t0,01
1 – 2	103	3	104	5,001	9,537	1,62	1,98	2,62
1 – 3	103	30	131	10,125	1,197	9,26	1,98	2,61
1 – 4	103	17	118	13,121	1,905	9,51	1,98	2,62
2 – 3	3	30	31	5,123	10,193	1,60	2,04	2,74
2 – 4	3	17	18	8,120	10,902	2,46	2,10	2,88
3 – 4	30	17	45	2,996	2,562	1,87	2,01	2,69

Значимые разности, для которых t_ > t_0,05 , выделены в таблице, откуда видно, что 1-я группа значимо отличается от 3-й и 4-й, 2-я группа значимо отличается от 4-й. Выводам этим явно не хватает наглядности. Трудно представить себе общую картину, особенно при сравнении большого количества групп (например, для 10 групп будет уже 45 сравнений).

Более наглядным является графическое сравнение интервальных оценок центров подсовокупностей (выборок), для чего для каждой группы следует вычислить границы 95%-ных доверительных интервалов , где – так называемая, "наименьшая существенная разность"; а_k – центр подсовокупности.

Группы	nk	Средние	HCPk	Нижние	Верхние
1	103	32,368	1,012	31,356	33,380
2	3	27,367	5,928	21,4389	33,295
3	30	22,243	1,875	20,369	24,118
4	17	19,247	2,490	16,757	21,738

В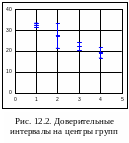 этой табличке определены Нижние и Верхние границы доверительных интервалов. На рис. 12.2 эти интервалы изображены в одном масштабе. Картина во многом проясни­лась. Группа 2 содержала всего 3 наблюдения, и доверительный интервал для оценки центра этой подсовокупности получился очень широким – он перекрывает доверительные интервалы для групп 1 и 3 (для сравнения 2-й и 4-й групп понадобилось дополнительное исследование). Чем больше наблюдений в группе, тем уже доверительный интервал, тем более определенные заключения можно сделать. По данному обследованию можно заключить, что группа 1 значимо отличается от групп 3 и 4. Что касается групп 3 и 4, то для них нуль-гипотеза об отсутствии значимых различий не может быть отвергнута – их доверительные интервалы перекрываются.

В данном примере ясность графического анализа была обусловлена малым количеством сравниваемых групп и тем, что эти группы были расположены регулярно в порядке убывания результативного признака.

Группы	nk	Средние	Однородные группы
4	17	19,247	
3	30	22,243		
2	3	27,367			
1	103	32,368			

Академик Б.А. Доспехов предложил еще более наглядное представление резуль­татов анализа. Группы должны быть отсор­тированы в порядке возрастания (или убывания) результативного признака (сред­них по группам). Далее строится символьная диаграмма (это проще, чем рисунок) из нескольких рядов звездочек. Если между некоторыми группами нет значимых различий, они помечаются звездочками в одном вертикальном ряду (однородные группы).