Вопросы для самопроверки

1. Что такое "состоятельность" оценок?

2. Что такое "несмещенность" оценок?

3. Что такое "сумма квадратов" (отклонений)?

4. Что такое "число степеней свободы"?

5. Привести формулу для несмещенной оценки дисперсии.

6. Что такое "эффективность" оценок?

7. Как оцениваются параметры распределения? Какие для этого существуют методы:

8. Что такое "статистики"?

9. Как выбирается зона чисто случайного изменеия статистики?

10. Как обозначаются критические значения статистик для несиммет­ричных распределений?

11. Как обозначаются критические значения статистик для симметрич­ных распределений?

12. Что такое "зона неопределенности критерия"?

Лекция 11. Критерии согласия Критерий согласия Пирсона

С помощью "критериев согласия" проверяют гипотезу о соответствии эмпирического распределения предполагаемому теоретическому закону, например, наиболее часто проверяют, можно ли считать наблюдаемое распределение нормальным.

Самый распространенный критерий согласия предложил К. Пирсон, который доказал, что если величины x_i распределены по стандартному нормальному закону x_i ~ N(0, 1) с характеристиками М(x_i) = 0 и (x_i) = 1, то сумма их квадратов имеет гамма-распределение с вполне определенными параметрами: 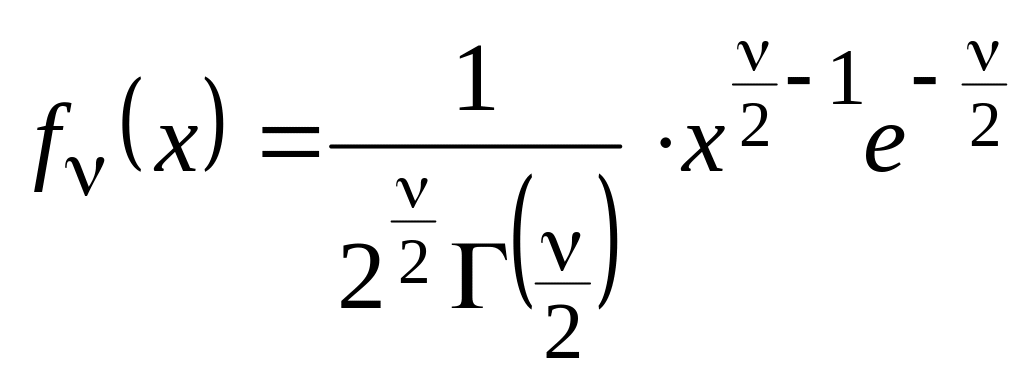. Этот частный случай гамма-распределения называется распределением Пирсона "Хи-квадрат". В общем виде гамма-распределение зависит от двух параметров ( и ). Ранее (при изучении композиций случайных величин) мы уже встречались с одним частным случаем гамма-распределения – распределением Эрланга с целочисленным параметром  = m. В распределении Пирсона оба параметра – полуцелые:  = ¹ / ₂ ,  = ^ / ₂ , где  = df – число степеней свободы (ЧСС) системы случайных величин {x_i} (для независимых величин df = n, a для зависимых df = n – Число Связей). Факториал ( – 1)! для дробных значений  в нашей научной литературе обозначается как – это гамма-функция, для кото­рой выполняется соотношение (+1) = (). В частности, , .

Закон распределения Пирсона – однопараметрический (зависит только от параметра  = df). Характеристики закона М(²) = , D(²) = 2. Типичный график дифференциальной функции распределения показан на рис. 11.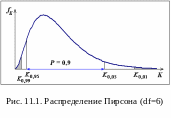 1, где K = ² . Для каждого значения  = df составлены таблицы квантилей . Зоной случайного изменения ²  является интервал (так называемый, 90%-ный доверительный интервал). При увеличении df распределение Пирсона приближается к нормальному, поэтому таблицы квантилей составлены только для df  30.

Для проверки гипотезы о согласии эмпирического распределения предполагаемому теоретическому закону Пирсон составил статистику (критерий), которая опять обозначается ²  :

,

где m_j – наблюдаемые частоты попадания случайной величины в интервалы s_j–1 < X  s_j , – ожидаемые частоты по предполагаемому теоретическому закону, в котором неизвестные параметры заменены на их эмпирические оценки. Структура статистики Пирсона – это сумма квадратов отклонений частот от их ожидаемых значений с весами (отклонения в одну-две единицы существенны для малых и не существенны для больших ).

Покажем, что при выполнении некоторых условий статистика Пирсона распределена по закону ² . Существует некоторая вероятность p_j попадания наблюдений в интервал (s_j–1 , s_j ]. Количество таких наблюдений (частота m_j) распределено по закону Бернулли с характеристиками M(m_j) = np_j  и D(m_j) = np_jq_j =  np_j(1 – p_j). При n  30, np_j  5 распределение Бернулли уже можно считать нормальным (распределением Лапласа) и тогда величина

будет распределена по закону ² . Если интервалы (s_j–1 , s_j ] достаточно узкие, настолько, чтобы можно было пренебречь малыми вероятностями p_j < 0,1 по сравнению с единицей, то получаем комплекс

,

который распределен по закону ²  при m_j  5, но при m_j < 0,1n (в каждый интервал должно попасть не менее 5-и наблюдений, но меньше 10% от объема выборки). Эти два несколько противоречивых требования могут быть выполнены одновременно только для выборок большого объема n > 200.

Теоретические вероятности попадания наблюдений в заданные интервалы вычисляются с помощью интегральной функции предполагаемого закона , а ожидаемые частоты – по формуле .

Отсюда получаем статистику Пирсона в стандартном виде . Если снять обременительное требование m_j < 0,1n, то статистика слегка усложняется 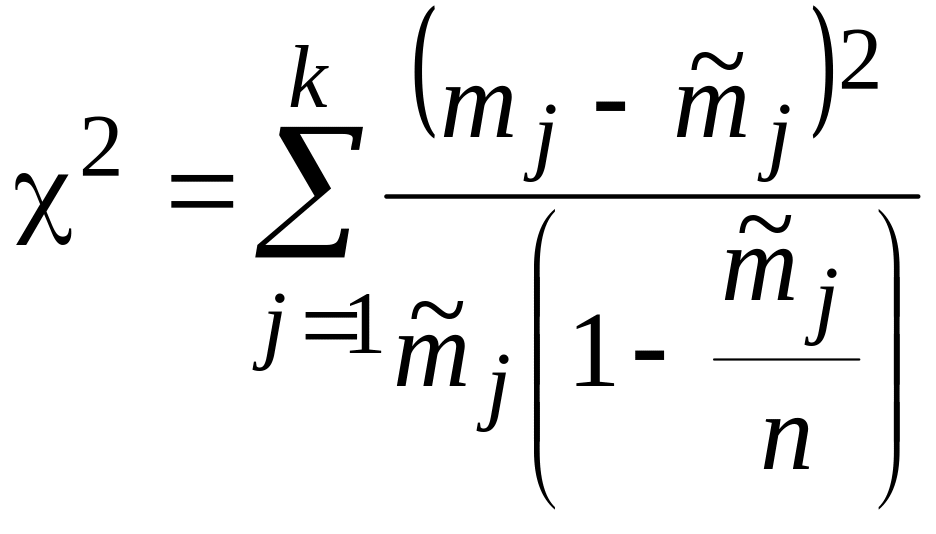, но теперь ее можно применять для выборок умеренного объема 30  n < 200.

Замена p_j на приводит к тому, что отклонения частот больше не будут независимыми, на них будут наложены две или три связи. Действительно, т.к. (если это не так, следует расширить крайние интервалы – еще одно условие правильного применения критерия Пирсона), то получается, что – сумма всех отклонений равна нулю. При оценке параметров предполагаемого закона методом моментов мы приравниваем теоретические характеристики их выборочным оценкам. Если закон однопараметрический (Пуассона или показательный), один параметр закона оценивается из равенства , откуда получаем еще одну связь , где X_j – центры интервалов. При проверке согласия распределения с однопараметрическим законом число степеней свободы равно df = n – 2. Большинство теоретических законов распределения – двухпараметрические (Бернулли, нормальный, логнормальный, равномер­ный, гамма), для них оценку второго параметра получаем, приравнивая дисперсии , что приводит еще к одной связи , откуда для двухпараметрических законов df = n – 3.

Для данного числа степеней свободы по таблицам Пирсона находят квантили . Если окажется, что вычисленное значение статистики хи-квадрат находится в пределах , нуль-гипотеза о случайности расхождений между наблюдаемыми и ожидаемыми частотами не может быть отвергнута; предполагаемый теоретический закон не противоречит данным; можно считать, что он именно такой и можно использовать его для дальнейших вычислений. Уровень доверия нашего заключения Р = 0,9 (90%). Если окажется, что вычисленное значение статистики хи-квадрат больше большей границы , нуль-гипотеза отвергается; предполагаемый теоретический закон не согласуется с данными, расхождения между наблюдаемыми и ожидаемыми частотами слишком велики, распределение неудовлетворительно описывается этим законом. Однако нуль-гипотеза отвергается также при слишком хорошем соответствии, когда вычисленное значение статистики хи-квадрат оказывается меньше меньшей границы ; в этом случае мы сомневаемся в достоверности данных, по всей видимости, здесь имеется какая-то фальсификация; вероятность такого хорошего соответствия при справедливости нуль-гипотезы меньше 1% , а такое событие является практически невероятным (невозможным).

Рассмотрим пример применения критерия согласия Пирсона.

Н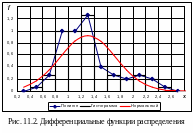 а рис. 11.2 изображены гистограмма, полигон (графичес­ки сглаженная гистограмма) и кривая нормального распределе­ния, параметры которой оценены методом моментов. Можно ли считать, что эмпирическое распределение – нормальное?

Ниже приведен интерваль­ный вариационный ряд с шагом группировки h = 0,2. Сумма наблюдаемых частот равна n = m_j = 75, оценки характеристик: , s_x = 0,433.

Х	0,5	0,7	0,9	1,1	1,3	1,5	1,7	1,9	2,1	2,3	2,5
	0,4–0,6	0,6–0,8	0,8–1,0	1,0–1,2	1,2–1,4	1,4–1,6	1,6–1,8	1,8–2,0	2,0–2,2	2,2–2,4	2,4–2,6
m	1	4	15	15	19	6	4	3	4	3	1
	0,034	0,072	0,121	0,165	0,183	0,164	0,119	0,070	0,034	0,013	0,004
	0,053	0,072	0,121	0,165	0,183	0,164	0,119	0,070	0,034	0,013	0,005
	4,0	5,4	9,0	12,4	13,7	12,3	9,0	5,3	2,5	1,0	0,4
		9,4	9,0	12,4	13,7	12,3	9,0	9,2
m		5	15	15	19	6	4	11
Хи-кв		2,06	4,00	0,55	2,05	3,23	2,78	0,35
Исправ		2,36	4,55	0,65	2,51	3,86	3,16	0,40

В строке (верхний ряд цифр) вычислены вероятности попадания наблюдений в каждый интервал по формуле , где Ф – интегральная функция Лапласа, . Сумма этих вероятностей оказалась равной 0,979, т.е. меньше 1. Расширяем крайние интервалы и для первого интервала (с центром Х = 0,5) вычисляем , а для последнего (с центром Х = 2,5) – . Исправленные значения приведены в строке (нижний ряд цифр). Сумма исправленных вероятностей равна единице.

В строке (верхний ряд цифр) вычислены теоретические частоты, которые ожидаются согласно нормальному распределению. Сумма этих частот равна n = 75. Для правильного применения критерия Пирсона малонасыщенные интервалы следует объединить с соседними, так чтобы в каждый укрупненный интервал попало не менее 5-и наблюдений. Укрупняем первые два интервала и последние четыре (при укрупнении частоты складываются). Укрупненные теоретические частоты записаны в строке (нижний ряд цифр). В следующей строке приведены укрупненные наблюдаемые частоты m.

Далее в строке "Хи-кв" вычислены отдельные слагаемые , а в последней строке "Исправ" – с поправкой на малый объем выборки .

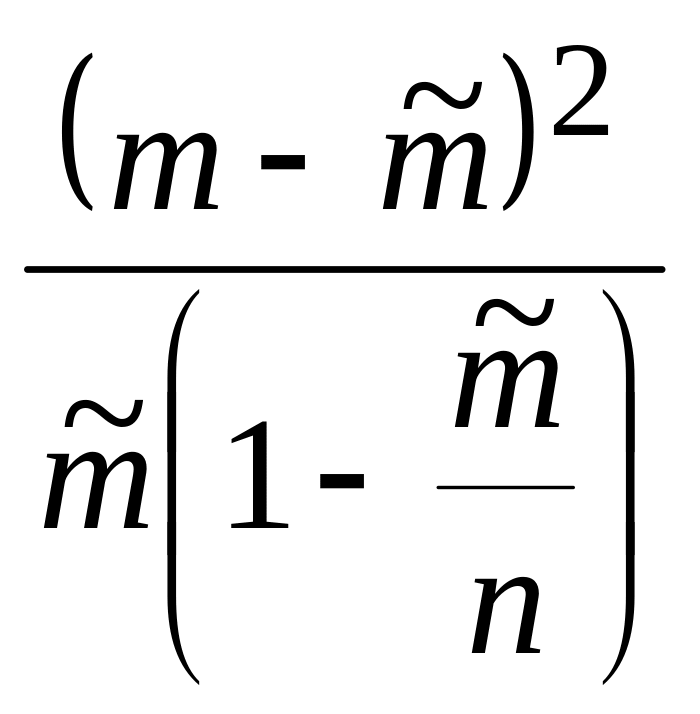Стандартное значение критерия получилось равным ² = 15,01. Исправленное значение оказалось несколько большим ² = 17,48. У нас было k = 7 укрупненных интервалов (7 пар частот для сравнения). Нормальный закон – двухпараметрический, поэтому число степеней свободы равно df = 7 – 3 = 4. Для этого значения числа степеней свободы из таблицы Пирсона выписываем критические значения: . . Для n > 30 можно использовать таблицы для нормального закона с M = df = 4 и ² = 2df = 8. Оба вычисленных значения статистики Пирсона ²  (стандартная – 15,01 и исправленная – 17,48) оказались больше большей критической границы (13,28), следовательно, гипотеза о нормальности распределения отвергается.