Статистические критерии

Наряду с оценками характеристик и параметров вводят еще некоторые числовые комплексы К, составленные из данных наблюдений. Эти комплексы зависят от состава случайной выборки и поэтому также являются случайными величинами. Если известен (изучен) закон распределения К, то такие комплексы называются "статистиками" или "критериями". Известны статистики Пирсона, Стьюдента, Фишера (по именам ученых, установивших закон распределения того или иного комплекса). Многие оценки можно называть "статистиками", показывая этим, что нам известны законы распределения таких оценок при изменении состава выборки.

Определим зону чисто случайного изменения критерия К, используя практический принцип невозможности редких событий. Выбираем "уровень значимости" , малый настолько, что мы сомневаемся в случайной природе появления события с такой малой вероятностью; мы более склонны считать, что наблюдаемое редкое событие вызванно какими-то внешними воздействиями, это "что-то означает" (вот откуда терминология "уровень значимости"). Обычно принимается уровень значимости 0,1, 0,05 или 0,01. Вероятность противоположного события P = 1 –  назывется "уровнем дове­рия". Обычно принимают уровень доверия 0,9, 0,95 или 0,99. Зону чисто случайного изменения критерия составляют все его значения, которые появляются с вероятностью, большей уровня значимости.

Далее все зависит от особенностей проблемы, для которой составлен тот или иной кртерий. Существуют односторонние критерии, когда мы сомневаемся в случайном появлении слишком больших (или, наоборот, слишком малых) значений К. Для правостороннего критерия (рис. 9.3 а), зная распределение статистики К, находим квантиль К_ из условия Р(K > К_) = , или F(К_) = Р(K  К_) = 1 – . Площадь под дифференциальной кривой f_K справа от К_ равна . Если для наших данных окажется, что вычисленное значение K больше критического К_ , "нуль-гипотеза" о случайности изменения К отвергается и принимается противоположная (альтернативная) гипотеза о неслучайном появлении столь большого К. Если для наших данных окажется, что вычисленное значение K меньше критического К_ , "нуль-гипотеза" о случайности изменения К "не может быть отвергнута".

а б

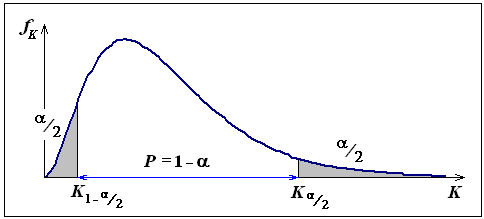
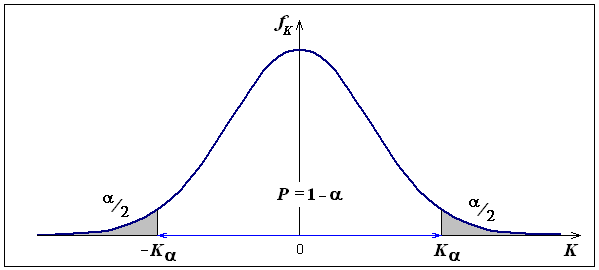
Рис. 9.3. Критическая зона для одностороннего (а) и двустороннего (б) критериев

Для двустороннего критерия (когда сомнительны большие случайные отклонения К и вправо и влево), вычисляются квантили и . Площади под дифференциальной кривой f_K слева от и справа от одинаковы и равны  ^ /₂  (рис. 9.3 б). "Нуль-гипотеза" о случайности измене­ния К не может быть отвергнута, если вычисленное значение критерия попадает в интервал .

Так должно быть и для симметричных распределений статистики К, но в этом случае приняны не совсем правильные обозначения. Критическое значение К_ теперь определяется из условия Р(|K | > К_) = . Заметим, что при этих обозначениях площадь под дифференциальной кривой f_K справа от К_ равна  ^ /₂  (рис. 10.4). Это не совсем правильно, но общепринято.

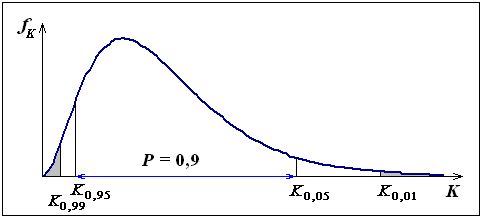
Рис. 9.4. Случай симметричного распределения статистики К	Рис. 9.5. Два уровня значимости (для принятия и отбрасывания 0-гипотезы)

Границы между областью принятия и областью отбрасывания нуль-гипотезы несколько размыты (см. рис. 9.5). Любой статистический кртерий имеет некоторую область неопределенности, поэтому рекомендуется использовать сразу два уровня значимости (один для принятия, другой для отбрасывания нуль-гипотезы). Мы уверены, что события с вероятностью   0,01 случайно не происходят, поэтому принимаем такой уровень значимости для отбрасывания нуль-гипотезы. В то же время, вероятность  > 0,05 уже не может считаться "малой", поэтому этот уровень значимости используется для принятия нуль-гипотезы.

Нас могут интересовать самые различные вещи, например, есть ли существенные различия между урожайностью разных сортов пшеницы, между эффективностью различных лекарственных препаратов, однотипной продукцией различных предприятий; нас может интересовать, есть ли значимое воздействие некоторых наших мероприятий на повышение качества и количества производимого продукта, нас крайне интересует надежность и безопасность, здоровье и сохранение среды обитания. Чтобы получить внятные ответы на наши запросы, формулируется соответствующая "нуль-гипотеза", которая скептически утверждает, что никакого систематического воздействия нет, вся изменчивость определяется чисто случайными флуктуациями, нет никакого значимого различия между сравниваемыми сортами, продукцией разных предприятий, наши лекарства и наши мероприяния не приносят никакого эффекта. Мы должны оценить вероятность появления наших данных при справедливости "нуль-гипотезы" и если эта вероятность не окажется достаточно малой, мы вынуждены будем сделать огорчительное заключение: "Нуль-гипотеза не может быть отвергнута"; данных мало, чтобы надежно заявить противоположное; такие эффекты могут появляться чисто случайно. Мы вовсе не утверждаем, что лекарства действительно неэффективные, что сравниваемая продукция действительно эквивалентна и т.п, мы расписываемся в собственной беспомощности – по имеющимся данным ничего определенного сказать нельзя.

Но если вероятность появления данных при справедливости нуль-гипотезы окажется меньше определенного уровня, то "нуль-гипотеза отвергается" и принимается противоположное утверждение, которое называется "альтернативной гипотезой". При правильно поставленных вопросах альтернативная гипотеза может утверждать, что между подсовокупностями имеются значимые различия (в любую сторону), а может более определенно утверждать, что альтернативное значение параметра больше (или, наоборот, меньше) того, которое свойственно при нуль-гипотезе. Все истины, которые установлены экспериментально, получены в опытах, где нуль-гипотеза была отвергнута (найдены контрпримеры). Тонкий знаток и ценитель природы, писатель М. Пришвин заметил: "«Да» природы – условное и еле слышимое. «Нет» природы – ясное и категоричное".

Государственными стандартами установлено, какую вероятность можно и должно считать малой. Это "уровень значимости"   0,01, который является вероятностью "ошибки 1-го рода" – вероятности ошибочно отвергнуть правильную 0-гипотезу. В то же время, вероятность  > 0,05 уже не может считаться "малой", иначе мы допустим "ошибку 2-го рода" – ошибочно примем неверную альтернативную гипотезу (в юстиции также различают ошибки "наказать невиновного" и "упустить виновника"; в приемочном контроле различают "риск производителя", когда на основе недостаточного выборочного обследования бракуют всю партию годной продукции, и "риск потребителя" – когда принимается партия некондицион­ной продукции).

Поэтому если вероятность чисто случайного появления наших данных больше 5% , делается стандартное заключение "нуль-гипотеза не может быть отвергнута" (иногда говорят, "0-гипотеза принимается"); если вероятность оказалась меньше 1% , то "нуль-гипотеза отвергается"; но если эта вероятность больше 1%  и меньше 5% , делается более осторожное заключение: "Нуль-гипотеза принимается (или отвергается) при 5%-м уровне значимости". Наши заключения могут задевать чьи-то интересы, и в последнем спорном случае на нас могут оказывать определенное давление в пользу того или иного вывода; именно поэтому необходима оговорка о 5%-м уровне значимости.