Оценка параметров распределения

До сих пор мы рассматривали оценки характеристик распределения и для самых распространенных характеристик получили готовые вычислитель­ные формулы.

Переходим к оценкам параметров закона распределения (в будущем будем оценивать также параметры эконометрических моделей).

Любой закон распределения зависит от небольшого количества параметров. Если значения параметров известны, то можно вычислить характеристики данного закона распределения. "Параметры распределения" и "характеристики распределения" – это разные вещи. Например, равномер­ный закон зависит от двух параметров a и b; зная значения этих параметров, можно вычислить характеристики равномерного распределения, например, математическое ожидание и стандартное отклонение: ; .

Чтобы получить оценки параметров, применяется один их трех методов: метод моментов, метод максимального правдоподобия и метод наименьших квадратов.

Метод моментов – самый простой из них. Согласно этому методу, надо теоретические характеристики распределения (они являются функциями неизвестных параметров) приравнять их выборочным оценкам. В результате получаем систему уравнений для определения оценок параметров.

Например, чтобы найти два параметра равномерного закона приравниваем две важнейшие характеристики (обычно это математическое ожидание и стандартное отклонение) их выборочным оценкам (среднему и несмещенной оценке стандартного отклонения):

.

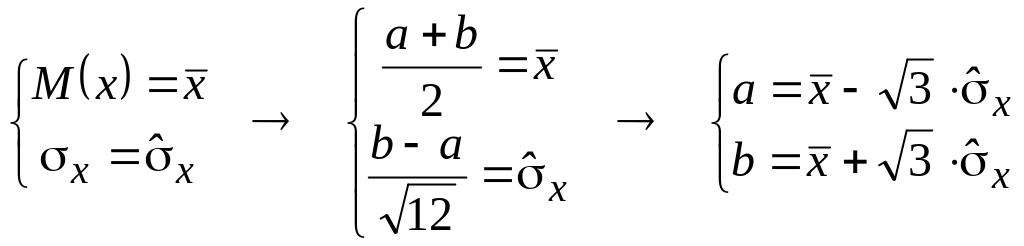Мы составили систему двух уравнений относительно двух неизвестных параметров равномерного распределения и получили оценки этих парамет­ров. Резонно их обозначать , или же, наоборот, теоретические параметры закона переобозначить греческими буквами , . Иногда в одном и том же тексте одновременно используются теоретическая функция распределения (например, плотность вероятности) f(x_j), ее эмпирическая оценка (гистограм­ма) и теоретическая функция, в которой параметры заменены на их оценки. Для этой последней разновидности оценки функции распределения можно ввести еще какое-нибудь свое обозначение, например, .

У нормального закона параметры совпадают с основными характерис­тиками, поэтому систему уравнений не придется решать:

.

Показательный закон зависит от одного параметра , характеристики распределения выражаются через этот параметр: Если их теоретических соображений ожидается показательное рапределение и , то параметр определяется из одного уравнеия .

Метод максимального правдоподобия – считается наиболее обосно­ванным и пропагадируется как (не побоимся этого слова) самый модный (в настоящее время) способ определения параметров. Заключается он в следующем: для всей системы наблюдений {x_i} составляется "функция правдоподобия" – вероятность или плотность вероятности совместного появления такой системы данных. Функция правдоподобия зависит от параметров предполагаемого закона распределения. Эти параметры следует определять из условий максимума функции прадоподобия.

Например, предполагая показательное распределение, найдем наиболее правдоподобную оценку параметра . Функция плотности вероятности этого распределения для наблюдения x_i имеет вид: f(x_i) = exp{–x_i}. Для независимых наблюдений дифференциальная функция их совместного распределения получается как произведение дифференциальных функций: f(x₁, x₂, … , x_n} = П(exp{–x_i}) = ⁿexp{–x_i}. Обычно функцию правдо­подобия принимают равной логарифму натуральному от этого выражения: Ф() = nln() – x_i . Приравниваем нулю первую производную от функции прабдоподобия , откуда получаем . Именно такую оценку параметра мы получили ранее методом моментов.

Для нормального закона 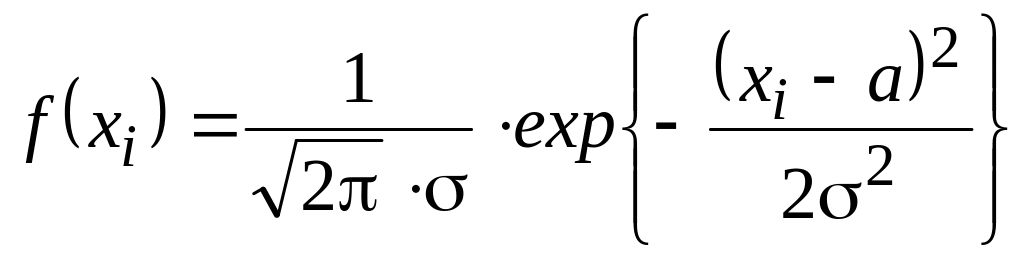, тогда функция правдоподобия (логарифм от произведения функций f(x_i)) будет равна

,

где постоянное слагаемое отброшено.

Приравниваем нулю частную производную функции правдоподобия по параметру а: , откуда . Правдоподобная оценка параметра а совпала с оценкой по методу моментов.

Приравниваем нулю частную производную функции правдоподобия по параметру : , откуда . Правдоподобная оценка параметра ² оказалась равна обычной (смещенной) оценке дисперсии.

Метод наименьших квадратов – применяется, в основном, в тех случаях, когда модель зависит от параметров линейно. Мы будем использовать этот метод для определения параметров регрессионных моделей. Он будет подробно описан в разделе "Регрессионный анализ".