Вопросы для самопроверки

1. Что такое "совокупность", "генеральная совокупность", "выборка"?

2. Что такое "репрезентативность"? Приведите примеры отсутствия репрезентативности.

3. Перечислите основные проблемы математической статистики.

4. Как составляются представительные выборки данных?

5. Что такое "статистические оценки". Перечислите основные статистические оценки характеристик и функций распределения.

6. Напишите сравнительные формулы для характеристик случайной величины и для их статистистических оценок.

7. Как составляется интервальный вариационный ряд?

8. Что такое "гистограмма"? Как она строится и преобразуется при укрупнении интервалов?

9. Что такое "полигон" для непрерывной случайной величины? Чему равняется его площадь? Что означает часть площади полигона (гистограммы) на определенном интервале варьирования случайной величины?

10. Что такое "кумулята"? Как она строится для непрерывной случайной величины? Для дискретной случайной величины?

12. Как с помощью кумуляты находятся значения (оценки) квартилей?

13. Что показывает блочная диаграмма Тьюкки?

Лекция 10. Свойства статистических оценок

Доброкачественные оценки должны быть "состоятельными", "несмещенными" и "эффективными".

Оценка b генеральной характеристики  называется состоятельной, если при увеличении объема выборки она приближается к своей генеральной характеристике: . Если это свойство не выполняется, оценка является дефектной. Несостоятельными оценками пользоваться нельзя.

Все наши предыдущие оценки были состоятельными.

Доказано, что (на основании закона больших чисел) относительная частота стремится к вероятности, а среднее стремится к математическому ожиданию , . Иными словами, эти оценки – состоятель­ные.

Но тогда будут состоятельными все оценки, основанные на замене вероятностей на относительные частоты, а математических ожиданий – на средние.

Так, для оценки дисперсии в пределе (n  ) получаем:

.

Оценка b генеральной характеристики  называется несмещенной, если М(b) = . Несмещенные оценки не имеют систематических ошибок (смещений).

Ранее уже было доказано (в разделе о распределении среднего X_cp), что . Первую формулу теперь можно трактовать так: выборочное среднее есть несмещенная оценка математического ожидания.

Н а рис. 10.1 изображено рассея­ние исходных данных вокруг своего центра М(х). Предполагается, что из этих данных случайным образом отбираются по n элементов в различные выборки и вычисляются их средние. Средние различных случай­ных выборок рассеяны вокруг своего центра . Оказывается, что центр группировки выборочных средних совпадает с центром группировки исходных данных . Систематического смещения нет.

О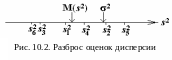 днако выборочная оценка дисперсии уже не обладает несмещенностью, она состоятельна, но систематически занижена (см. рис. 10.2). Дело в том, что в генеральной дисперсии рассматрива­ются отклонения от центра совокуп­ности, а в выборочной оценке – от центра выборки, а это не одно и то же: , .

Выведем формулу для расчета несмещенной оценки дисперсии.

Записываем формулы для дисперсии исходной случайной величины X, для дисперсии средних X_ср и для оценки дисперсии :

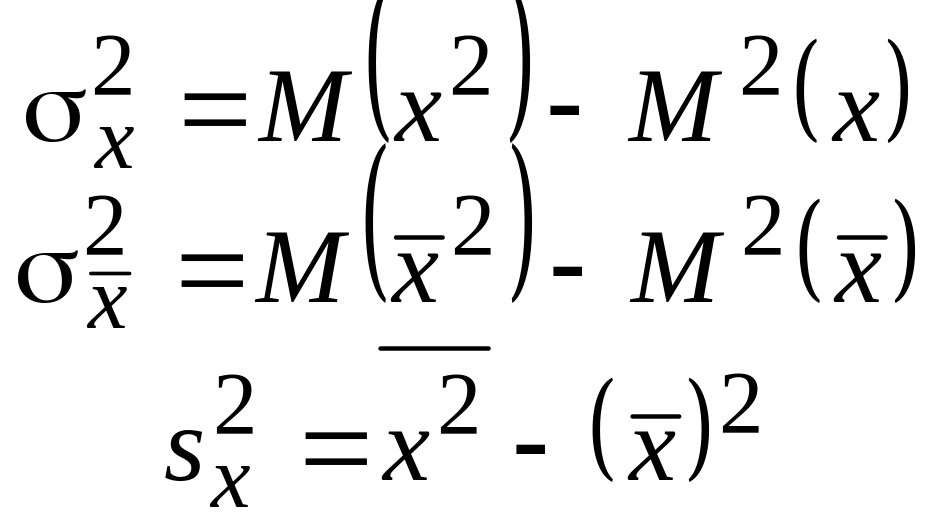
Вычисляем математическое ожидание от (определяем центр группировки выборочных оценок дисперсии):

.

При преобразованиях мы дважды использовали факт несмещенности оценки математического ожидания и в одном месте заменили на , а в другом месте, наоборот, заменили М(х) на . Получилось, что центр группировки выборочных оценок дисперсии всегда меньше свого предельного значения (генеральной дисперсии). Эта систематическая ошибка уменьшается с увеличением объема выборки (т.к. оценка дисперсии – состоятельная).

Продолжаем преобразования. Используем формулу для дисперсии среднего: . Введем поправку на несмещенность и получим несмещенную оценку дисперсии в виде:

.

Здесь – сумма квадратов n отклонений значений x_i от центра выборки (SS – summa of square – сумма квадратов). Однако не все n отклонений являются независимыми – их сумма всегда равна нулю (нулевое или центральное свойство среднего). Следовательно, независимых отклонений будет на единицу меньше, последнее отклонение всегда можно найти из выражения . Введем понятие "числа степеней свободы", которое равно разности количества значений случайной величины и числа наложенных на них линейных связей: ЧСС = df_x = n – l (df – degree of fridom – степени свободы); сейчас у нас одна связь – центральное свойство среднего, поэтому df_x = n – 1. Обычная оценка дисперсии равна отношению суммы квадратов (отклонений) к общему числу наблюдений, а несмещенная оценка дисперсии равна отношению суммы квадратов к числу степеней свободы.

Несмещенная оценка дисперсии состоятельная и не имеет система­тической ошибки. Это хорошо. К сожалению, за все приходится платить. Для несмещенных оценок дисперсии не выполняется важнейшее свойство дисперсии: несмещенная оценка дисперсии суммы независимых случайных величин больше не равна сумме оценок дисперсий отдельных слагаемых. Поэтому в той или иной форме используются оба вида оценок дисперсии (в англо-американской научной литературе обозначение закреплено за несмещенной оценкой дисперсии, но параллельно с ней оперируют с суммами квадратов SS_x , которые пропорциональны обычным оценкам дисперсии).

Оценка b генеральной характеристики  называется эффективной, если она имеет наименьшую дисперсию: .

Оценка – случайная величина, она зависит от состава случайной выборки. Если оценка неэффективная, то ее дисперсия недопустимо велика, что приводит к нестабильности результатов оценивания. Ошибка оценивания слагается из случайной ошибки и систематического смещения. Мы пытаемся использовать несмещенные оценки, для которых систематического смещения нет. Однако при этом иногда непомерно возрастает случайный разброс несмещенной оценки, из-за чего такая оценка оказывается явно неразумной (бывает даже, что оценка получается с противоположным знаком). Для пользователя слабым утешением является соображение о том, что явная ошибка оценивания является чисто случайной. Надо искать компромисс, можно допустить небольшую систематическую ошибку, лишь бы при этом суммарная ошибка оценивания была небольшой. Иными словами, пусть оценка будет немного смещенной, но более эффективной.

В регрессионном анализе несмещенные оценки параметров модели (по образному выражению К. Доугерти, оценки "инструментов экономического воздействия") получают в результате решения системы уравнений с корреляционной матрицей. Теоретически эта система всегда совместна (т.е. всегда имеет решение). Однако когда определитель системы линейных уравнений равен нулю (вырождение), то решение совмесной системы становится неединственным, а стандартные числовые алгоритмы решения просто не работают. Еще хуже, когда определитель нулю не равен, но близок к нему. Тогда формально будет получено единственное решение, но оно оказывается нестабильным настолько, что часто не имеет разумной интерпретации. Предложено к диагональным элементам корреляционной матрицы (они равны единице) добавлять малый параметр (число порядка 0,01 ‑ 0,05). Решение такой измененной системы уже будет стабильным, т.е. существенно уменьшается дисперсия случайной ошибки (этот эффект легко заметить, произведя серию решений с последовательно увеличивающимся параметром). Однако при добавлении малого параметра система-то уже становится другой (пусть близкой, но другой). Появляется систематическое смещение между решениями исходной и измененной системами уравнений. Иными словами, оценки параметров модели теряют свойство несмещенности, но становятся более эффективными, в результате чего общая (суммарная) ошибка существенно снижается.