Способы составления выборочных подсовокупностей

Правила составления выборок должны обеспечивать равные шансы любым элементам совокупности быть отборнными в выборку. Предложено несколько методик составления представительных выборок от самых простых до очень сложных.

Простой случайный отбор. Так называется способ, когда элементы совокупности отбираются в выборку случайным образом, например, с помощью таблицы случайных чисел. При этом предполагается, что выборка – однородная, а не представляет собой смесь нескольких пдсовокупностей.

Расслоенный случйный отбор. Предварительно выясняют, из каких заметно различающихся подсовокупностей (групп, классов, слоев) состоит общая совокупность, и определяют (хотя бы ориентировочно) объемы этих подсовокупностей (N₁ + N₂ + N₃ + … + N_k = N). Из каждой такой подсовокупности в выборку случайным образом отбираются элементы, количества которых пропорциональны объемам подсовокупностей (n₁ + n₂ + n₃ + … + n_k = n, где n_j = N_j).

На практике ориентируются соображениями на ограничения стоимости, времени и трудозатрат предварительного статистического обследования, поэтому часто выбирают упрощенные схемы отбора образцов, которые не гарантируют полной репрезентативности выборки. Однако в математической статистике данные будут анализироваться в предположении, что составленная выборка – реперезентативная (представительная).

Статистичекое оценивание

Доброкачественные оценки должны удовлетворять некоторым требованиям, о которых будет сказано ниже.

Сначала перечислим наиболее распространенные оценки характерис­тик распределения совокупности.

X	X1	X2	X3	…	Xk
m	m1	m2	m3	…	mk

Для выборочных данных {x_i} дискретной случайной величины подсчитывают частоты m_j повторяющихся значений X_j и составляют, так называемый, "вариационный ряд" в виде таблицы соответствия между дискретными значениями случайной величины и частотами их появления в выборке (m_j = n).

Относительные частоты являются стандартными оценками вероятностей p_j . Полигон относительных частот является приближением (оценкой) полигона вероятностей.

Среднее ("выборочное среднее") является оценкой математического ожидания ("генерального среднего") М(х). Среднее можно подсчитать или по исходным данным , или по сгруппированым .

Поскольку многие характеристики выражаются через математические ожидания, для получения оценок этих характеристик надо в соответствующих формулах заменить операторы математического ожидания на операторы среднего. Таким образом получаем оценки дисперсии, ковариации, коэффициента корреляции и многие другие:

Характеристики	Формулы	Оценки
Дисперсия
Ковариация	xy = M(xy) – M(x)M(y)
Коэффициент корреляции

В обозначениях оценок принято соглашение обозначать (по-возмо­жности) генеральные характеристики греческими буквами, а их выборочные оценки – соответствующими латинскими буквами, или же теми же символами, но с надстрочным знаком ^. Так, оценку дисперсии можно обозначать еще как . Иногда для одной и той же характеристики составляются разные оценки с разными свойствами, тогда разумно использовать разные обозначения для разных видов оценок. Далее мы будем обозначать через , так называемую, "несмещенную оценку дисперсии" (о которой будет сказано ниже).

Выборочные данные {x_i} непрерывной случайной величины группируют на k интервалов с определенными границами (s_j–1 , s_j]. Ширина интервалов может быть разной h_j = s_j – s_j–1 , центры интервалов обозначим .

X	X1	X2	X3	…	Xk
	s0–s1	s1–s2	s2–s3		sk–1–sk
m	m1	m2	m3	…	mk

Подсчитываются частоты m_j попадания выборочных данных {x_i} в эти интервалы и строится, так называемый, интервальный вариационный ряд. Данные, попадающие на края интервалов, надо относить к левому (меньшему) интервалу (имеются и другие рекомендации, но только одна из них согласуется с принятым выше определением функции распределения как F(x) = P(X  x)).

Теперь формулы для вычисления среднего и уже не эквивалентны, последняя формула (по сгруппированным данным) содержит дополнительно ошибку группировок, которая может быть существенной при малом числе интервалов. Если все интервалы – одинаковой ширины h = Const, то имеются рекомендации принимать число интервалов равным корню квадратному от объема выборки , или же по более сложной формуле: . Считается, что при k > 10 ошибки группировок сравнимы с другими видами ошибок, поэтому в этом случае допустимо пользоваться расчетами по сгруппированным данным, что существенно сокращает объем вычислительной работы при ручном счете.

Группировки нужны для описания закона распределения случайной величины. Ординаты эмпирической функции плотности вероятности (оценки дифференциальной функции распределения) вычисляются для центров интервалов . Поскольку все данные, попадающие в один интервал, округляются на его центр, а ошибки округления распределены по равномерному закону, то на каждом интервале (s_j–1 < x < s_j ) значения эмпирической плотности вероятности считаются постоянными и равными .

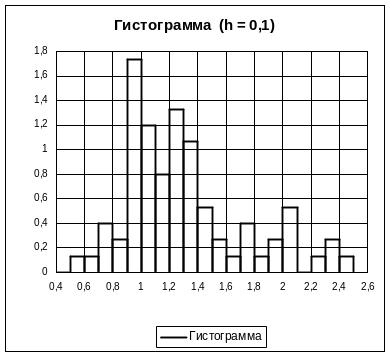
График этой столбчатой функции называется "гистограммой" (это оценка графика дифференциальной функции распределения). Площадь гистограммы равна единице. При выборе слишком большого числа интервалов (очень мелкого шага) в некоторые интервалы может попасть мало наблюдения и тогда гистограмма будет иметь неоправданные "провалы". В таком случае интервалы надо укрупнять, но так, чтобы площадь гистограммы не изменялась. На рис. 9.1 (а) приведена гистограмма с выбором слишком мелкого шага h = 0,1 (число интервалов k = 20 при объеме выборки n = 75). Видно много неоправданных провалов, а последние четыре наибольших наблюдения похожи на "выбросы".

а б

Рис. 9.1. Исходная и укрупненная гистограммы

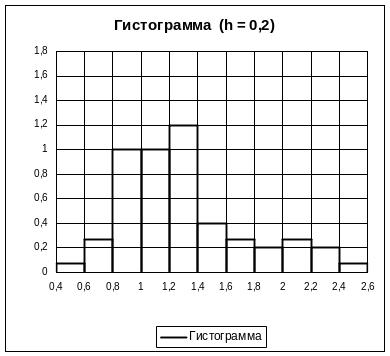
На рис. 9.1 (б) шаг был укрупнен вдвое h = 0,1 (k = 11), значения плотности вероятности в укрупненных интервалах вычислялись по формуле ; при укрупнении интервалов равной длины получается среднее ординат в объединяемых интервалах . Площадь гистограммы после укрупнения не изменилась. Для объема выборки n = 75 рекомендуется число интервалов ориентировочно принимать равным (k = 9); по формуле 15,3 получается большее значение (k = 15).

Середины столбиков гистограммы при интервалах равной длины можно соединить отрезками прямых и получить "полигон" (см. рис. 9.3). Полигон производит графическое сглаживание угловатой гистограммы и целиком ей эквивалентен. Площадь такого полигона равна едиице.

О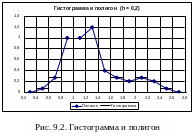 братите внимание на крайние интервалы – для постоения полигона к гистограмме были добавлены слева и справа пустые интервалы.

Бытует порочная практика вместо эмпирического графика плотности вероятности строить "гистограмму частот", или "гистограмму относительных частот". Для равноотстоящих интервалов ординаты всех этих видов "гистограмм" пропорциональны и вся разница сводится к разной градуировке оси ординат. Но если Вы не хотите неприятностей, никогда не пользуйтесь этими "гистограммами" – при необходимости укрупнять некоторые малонасыщенные интервалы вид таких "гистограмм" изменяется непредсказуемым образом. Далеко не всякая столбчатая диаграмма является гистограммой. В обычной столбчатой диаграмме ширина столбцов не имеет значения, она выбирается из декоративных соображений, а важны только высоты каждого столбца. Напротив, в гистограмме измеряют площади столбцов, а не их высоты – именно такой тип столбчатых диаграмм может называться "гистограммой"

Эмпирическая функция распределения (оценка интегральной функции распределения) называется "кумулятой" и строится по правым границам интервалов группировки. Ординаты кумуляты вычисляются по формуле . Для примера ниже приведен интервальный вариационный ряд, который был использован ранее для построения гистограммы.

X	0,2–0,4	0,4–0,6	0,6–0,8	0,8–1,0	1,0–1,2	1,2–1,4	1,4–1,6	1,6–1,8	1,8–2,0	2,0–2,2	2,2–2,4	2,4–2,6
m	0	1	4	15	15	19	6	4	3	4	3	1
m	0	1	5	20	35	54	60	64	67	71	74	75
	0	0,013	0,067	0,267	0,467	0,720	0,800	0,853	0,893	0,947	0,987	1

В третьей строке этой таблицы вычислены накопленные частоты m, а в четвертой – значения кумуляты (m / n) на правых краях интервалов.

Поскольку все данные, попадающие в один интервал, округляются на его центр, а ошибки округления распределены по равномерному закону, то в каждом интервале (s_j–1 < x < s_j ) значения эмпирической функции распределения изменяются по линейному закону.

Д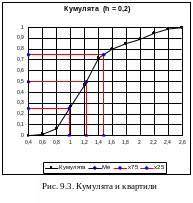 ля непрерывной случайной величины кумулята непрерывная кусочно-линейная (см. рис. 9.3). Напоминаем, что для дискретной случайной величины кумулята на интервалах (Х_j‑1 < x < Х_j ) сохраняет постоянные значения и изменяется скачками (ступеньками) только в заданных узлах x = Х_j . Нет никакой необходимости строить такой график, он нигде не используется. Напротив, кусочно-линейный график кумуляты для непрерывной случайной величины используется для расчета оценок квантилей. На рис. 9.3 показано, как определять оценки квартилей: на оси ординат задаем = 0,5; 0,25; 0,75 и, в соответствии с графиком, линейным интерполированием находим на оси абсцисс медиану Ме = х_0,5 = 1,23; нижнюю квартиль х_0,75 = 0,983; верхнюю квартиль х_0,25 = 1,48.

Квартили являются более надежными характеристиками положения, разброса и формы, нежели моменты распределения; они устойчивы к наличию "выбросов" – грубых ошибок некоторых наблюдений или описок (забыли десятичную запятую, перепутали сходные по начертанию цифры, например, 3 и 8, и т.п.).

А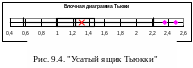 нглийский статистик Дж. Тьюкки предложил изображать распределение в виде блочной диаграммы "ящик и усы". "Ящик" (прямоугольник на рис. 9.4) ограничивает "лучшую половину наблюдений"; его границы – нижняя и верхняя квартили. Центральная линия показывает положение медианы (средней квартили). "Усы" показывают размах данных от x_min до x_max , но не более полутора межквартильного размаха от границ "ящика". Данные, которые выходят за границы "усов", считаются выбросами. В нашем примере имеется два выброса справа. Крестиком отмечено среднее , из-за выбросов оно сдвинуто вправо. Кстати, правило "3-х сигм" не обнаруживает этих выбросов (их отклонения от смещенного среднего не превышают 3-х сигм).