Двумерный нормальный закон

Плотность вероятности для этого закона описывается формулой:

,

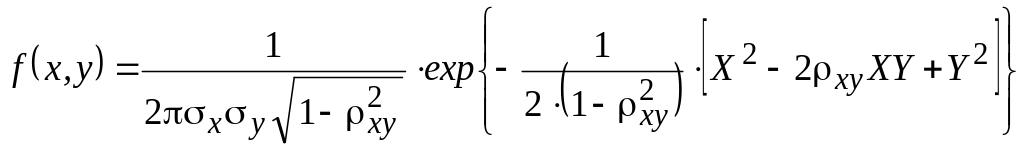где через Х и Y обозначены "стандартизованные" переменные

.

Двумерный нормальный закон зависит от пяти параметров, которые заодно являются его характеристиками: m_x , m_y , _x , _y , _xy .

Каждая компонента системы распределена по одномерному нормальному закону:

.

Поверхность нормального распределения для параметров m_x = 0; m_y = 0; _x = 1,5; _y = 1; _xy = 0,7 изображена на рис. 8.3 (а). Семейство линий уровня для двумерного нормального закона (рис. 8.3. б) представляют собой семейство эллипсов X² – 2_xyXY + Y² = Const. При _xy = 0 оси эллипсов параллельны координатным осям.

Условные распределения также подчиняются нормальному закону:

.

Интересно, что центры этих распределений (условные математические ожидания) линейно зависят от другой переменной:

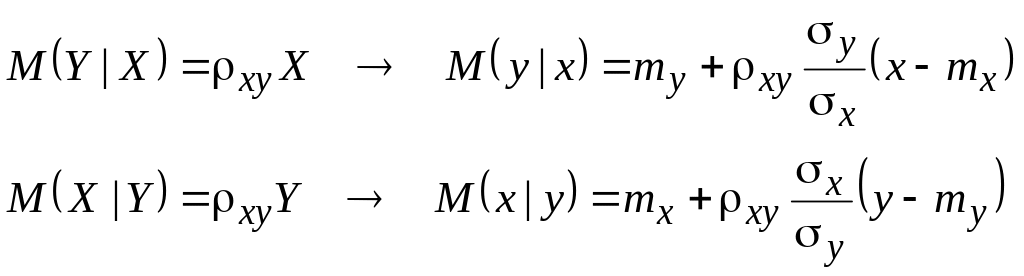
Эти линейные зависимости являются диаметрами эллипсов рассеяния, сопряженные семейству вертикальных и горозонтальных хорд соответсвен­но. Иными словами, М(y | x) представляет собой множество середин вертикальных хорд, а М(х | у) – горизонтальных хорд эллипсов. Оба диаметра при _xy  0 не совпадают с главными осями эллипса (см. рис. 8.3 б).

Выше уже указывалось, что для независимых случайных величин _xy = 0. Обратное утверждение в общем случае неверно – равенства _xy = 0 недостаточно, чтобы утверждать о независимости случайных величин X и Y, поэтому говорят, что при _xy = 0 случайные величины "не коррелированы".

Однако, если дополнительно известно, что закон совместного распре­деления – нормальный, то из условия _xy = 0 следует заключение о независимости компонент. Действительно, для _xy = 0 имеем:

;

Получили f(x, y) = f₁(x)f₂(y) – условие независимости X, Y.

Интересно, что в случае двумерного нормального закона меняются только центры условных распределений (условные математические ожида­ния), условные же дисперсии все одинаковые . При |_xy| = 1 D(y | x) = 0, т.е. разброса нет, зависимость – функциональная.

Вопросы для самопроверки

1. Приведите определение многомерной случайной величины.

2. Как можно задать распределение двумерной случайной величины?

3. Что такое "условные распределения"?

4. Как, зная двумерное распределение системы, найти законы распреде­ления ее компонентов?

5. Что такое "функция распределения" системы непрерывных случай­ных величин? Перечислите ее свойства.

6. Что такое "плотность вероятностей" для двумерных величин? Как эта функция связана с "функцией распределения"?

7. Перечислите основные характеристики двумерной случайной величины.

8. Что такое "ковариация", каковы ее свойства?

9. Что такое "коэффициент корреляции", каковы его свойства?

10. Чему равен коэффициент корреляции для независимых случайных величин?

11. Какие выводы можно сделать, если коэффициент корреляции равен нулю? Если он равен единице? Если он отрицательный?

12. Какие бывают типы связей?

13. Что такое "корреляционная зависимость"?

14. Какую зависимость характеризует коэффициент корреляции?

15. Сформулируйте двумерный нормальный закон распределения.

16. Что такое "эллипсы рассеяния"?

17. Каковы распределения компонент, если система величин имеет многомерное нормальное распределение?

18. Какими особенностями обладают условные распределения, если система величин имеет двумерное нормальное распределение?

19. Как связано условное математическое ожидание с фиксированным аргументом, если система величин имеет двумерное нормальное распределение? Дайте геометрическую интерпретацию.

20. Какова условная дисперсия, если система величин имеет двумерное нормальное распределение?