Закон распределения непрерывной двумерной случайной величины

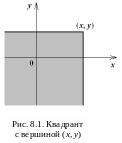
У ниверсальным способом задания случайной величины является ее "функция распределения": F(x, y) = P(X ≤ x; Y ≤ y) – вероятность того, что каждая компонента системы не превзойдет указанных значений x, y. Геометрически (см. рис. 8.1) это означает вероят­ность попадания случайной точки в квадрант с правой верхней вершиной в точке (x, y). Из определения функции распределения следует: 0  F(x, y)  1, F(‑, ) = F(, –) = F(–, –) = = 0, F(, ) = 1, F(x, ) = F(x) , F(, у) = F(у) .

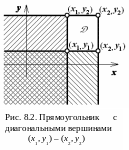
Рассмотрим вероятность попадания случайной точки M(x, y) в прямоугольник D с диагональными вершинами (х₁, у₁) – (х₂, у₂). Из рис. 8.2 находим, что эта вероятность равна:

P(M  D) = P(x₁ < X  x₂ , y₁ < Y  y₂ ) = = F(x₂ , y₂) – F(x₁ , y₂) – F(x₂ , y₁) + F(x₁ , y₁)

Вводим понятие "плотности вероятности" как отношение вероятности попадания случайной точки в какую-либо область к площади этой области. Для определения функции плотности вероятности f(x, y) в точке используем предельный переход:

.

Таким образом, функция плотности вероятности для двумерной случайной величины равна смешаной производной второго порядка от функции распределения

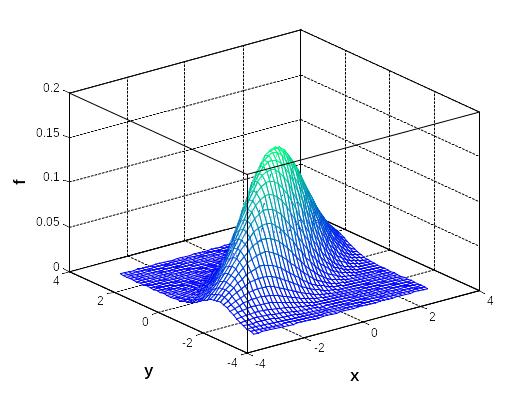
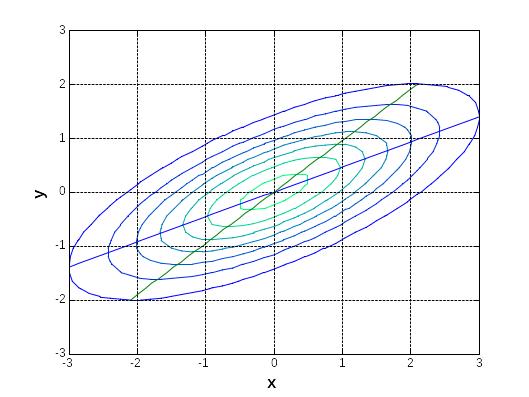
Геометрически двумерную функцию f(x, y) можно представить некоторой поверхностью – "поверхностью распеделения". На рис. 8.3 (а) для примера приведена такая поверхность для двумерного нормального закона (будет рассмотрен далее). Удобно изображать двумерные распределения линиями уровня – линиями равной плотности вероятности (см. рис. 8.3 б).

a б

Рис. 8.3. Двумерный график плотности вероятности нормального закона (а) с параметрами (m_x = 0; m_y = 0; _x = 1,5; _y = 1; _xy = 0,7) и семейство линий уровня f = Const (б)

Если отдельные компоненты, вхлдящие в систему, взаимно независимые, то по теореме умножения вероятностей имеем:

F(x, y) = P(X ≤ x; Y ≤ y) = P(X ≤ x)P(Y ≤ y) = F(x)F(y).

Дифференцируем это равенство по х и по у:

Таким образом, для независимых компонент плотность распределения системы случайных величин оказалась равной произведению плотностей распределения отдельных компонент.

Напоминаем, что случайные величины называются независимыми, если закон распределения каждой из них не зависит от того, какое значение приняла другая величина.

Зная плотность вероятности системы f(x, y), всегда можно найти распределение отдельных компонент:

.

Обратное в общем случае неверно – только для независимых компонент можно по их распределениям восстановить закон распределения всей системы.

Согласно общей теореме умножения вероятностей записываем:

f(x, y) = f₁(x)f₂(y | x) = f₂(y)f₁(x | y),

где условные плотности вероятностей f₂(y | x) и f₁(x | y) можно вычислить как отношения

.

Характеристики непрерывной двумерной величины

Все вычислительные формулы аналогичны формулам для вычисления характеристик дискретных величин, только дискретные суммы заменяются на интегралы:

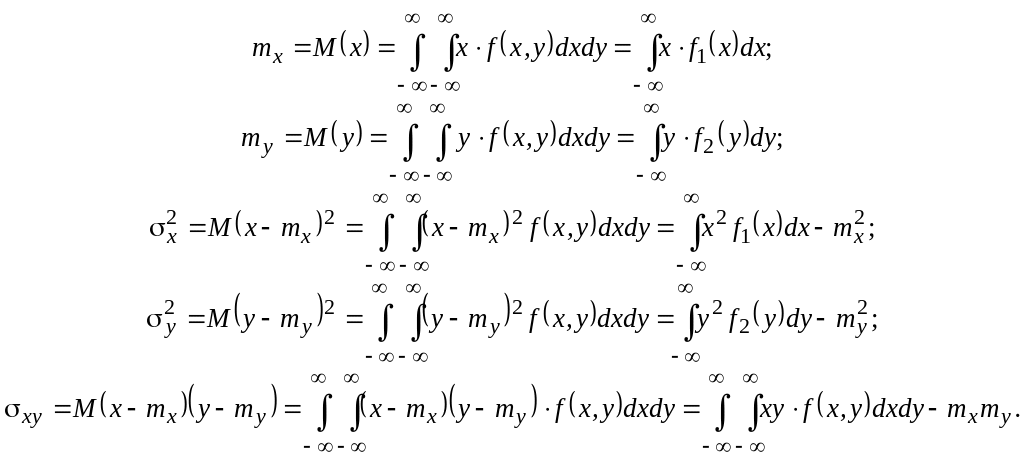
Если ковариация _ху отлична от нуля, вычисляются еще условные характеристики:

.

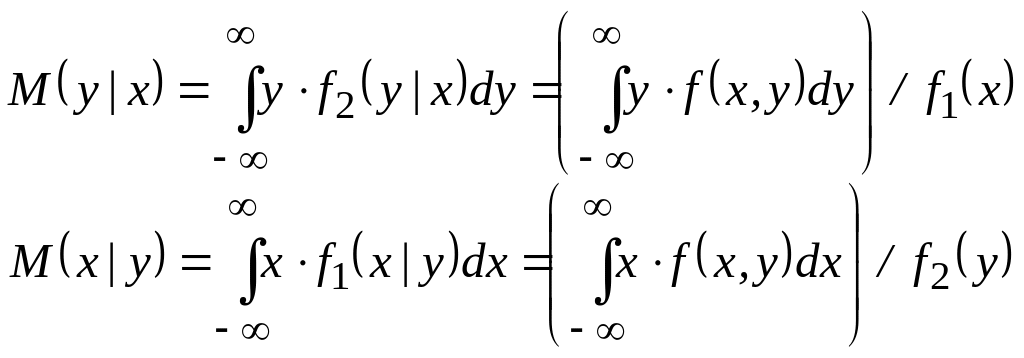Условные характеристики являются функциями другого аргумента.