Характеристики дискретной двумерной случайной величины

Кроме стандартных характеристик отдельно для каждой компоненты многомерной случайной величины:

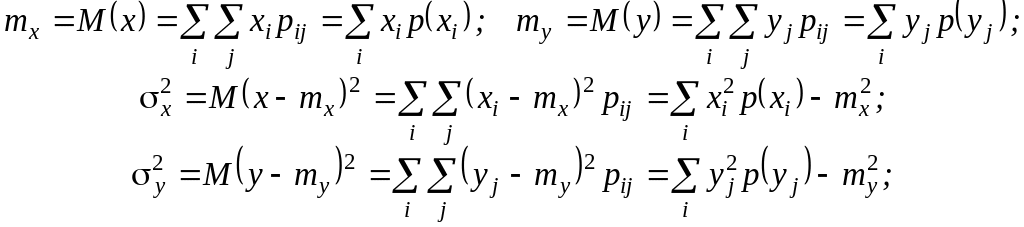
вычисляются еще смешанные центральные моменты, которые называются ковариациями (для двумерной величины имеется только одна ковариация – коэффициент совместной изменчивости х и у):

.

Дисперсии являются частным случаем ковариации при х = у:

_xx = _xx = M(x – m_x)² ; _yy = _yy = M(y – m_y)² .

Нормированный смешанный центральный момент (нормированная ковариация) называется "коэффициентом корреляции":

.

Коэффициент корреляции является мерой тесноты связи между х и у. Ранее уже было доказано, что для независимых случайных величин ковариация (и коэффициент корреляции) равны нулю.

Для любого столбца таблицы можно вычислить условные характерис­тики: математическое ожидание М(y | x_i) и дисперсию D(y | x_i):

.

Аналогично вычисляются условные характеристики для строк таблицы

.

Если множество значений двумерной величины представить точками с координатами (x_i , y_j) и весами (весовыми коэффициентами) p_ij , то условные математические ожидания М(y | x_i) будут представлять собою центры тяжести (средние взвешенные) в каждом вертикальном ряду таблицы для х = x_i , М(х | у_j) – в каждом горизонтальном ряду таблицы для у = у_j , точка с координатами (М(х), М(у)) – общий центр тяжести всей системы точек.

Для независимых случайных величин все условные характеристики одинаковы для всех рядов таблицы: М(y | x_i) = М(у) и все М(х | у_j) = М(х).

Введем некоторую классификацию типов связей (зависимостей).

Зависимость называется функциональной, если каждому значению аргумента (аргументов) соответствует единственное значение функции (каждому значению объясняющих переменных соответствует единственное значение результативного признака, случайного разброса нет).

Зависимость называется стохастической (статистической), если при изменении объясняющих переменных меняется закон распределения результативного признака (меняется его условное распределение) – меняется вид распределения или только его характеристики (условные математические ожидания, дисперсии и т.п.). Таким образом, в отличие от функциональной связи, при статистической зависимости нет однозначного соответствия между множеством значений аргументов и множеством значений функции.

Статистическая зависимость называется корреляционной, если при изменении аргумента меняется условное математическое ожидание функции (каждому значению объясняющих переменных соответствует свое среднее значение результативного признака). При корреляционной зависимости мы следим за изменением только одной характеристики – центра условного распределения (условного математического ожидания).

Корреляционная зависимость является частным случаем общей статистической зависимости. Естественно, существуют также иные виды статистических зависимостей не корреляционного типа, например, когда меняется условная дисперсия.

Коэффициент корреляции является мерой тесноты корреляционной связи; когда он равен нулю, корреляционной зависимости нет (все условные математические ожидания одинаковы). Однако при _ху = 0 могут быть иные виды статистической зависимости, поэтому из равенства нулю коэффициента корреляции еще нельзя утверждать, что случайные величины X, Y – независимые; говорят, что такие величины "не коррелированы".

Покажем, что максимальное значение коэффициента корреляции по абсолютной величине равно единице. Для этого рассмотрим дисперсию линейной комбинации , где _xy – ковариация: _xy = _x_y_xy . Отсюда получаем –1  _xy  1.

При |_xy| = 1 зависимость линейная функциональная (нет разброса).