Композиция распределений случайных величин

Распределение суммы независимых случайных величин называется "композицией распределений".

Сначала рассмотрим композицию распределений двух дискретных независимых случайных величин X, Y. Дискретная величина X определена на дискретном множестве значений х, которые появляются с вероятностями Р_х(х); если же значение х не принадлежит заданному дискретному множест­ву, будем считать его вероятность равной нулю. Аналогично условимся задавать закон распределения дискретной величины Y – если у не принадлежит заданному дискретному множеству значенийй Y, то его вероятность принимаем равной нулю, а если принадлежит, то Р_у(у). Вводим новую случайную величину Z = X + Y. Вероятность совместного появления конкретных слагаемых х, у вычисляется по теореме умножения Р_х(х)Р_у(у). Сумма z = x + y может появиться не одним способом; согласно аксиоме сложения, вероятности всех таких комбинаций х, у надо сложить:

.

Эту формулу можно переписать виде:

или

Для непрерывных случайных величин можно получить очень похожие формулы, где дискретная сумма заменяется на интеграл:

или .

Эти интегралы иногда называются "сверткой".

Пример 1. Найдем закон распределения двух случайных величин, каж­дая из которых распределена по показательному закону f₁(x) = e^–x , x  0:

.

Здесь бесконечные пределы интегрирования заменены на 0 и х, т.к. подинтегральная функция отлична от нуля только для у  0 и (х – у)  0.

Теперь найдем закон распределения трех слагаемых, каждая из которых распределена по показательному закону:

.

Аналогичными выкладками получаем:

В общем виде получается гамма-распределение с целочисленным параметром m (распределение Эрланга):

.

Графики этого распределения при различных значениях параметра m приведены на рис. 7.1 (б).

Гамма-распределение обладает своеобразной устойчивостью – компо­зиция гамма-распределений с параметрами m₁ и m₂ снова приводит к гамма-распределению с параметром m = m₁ + m₂ . С увеличением m это распределе­ние приближается к нормальному.

Нормальное распределение также обладает устойчивостью – компози­ция двух нормальных распределений N(a₁ ; ₁) и N(a₂ ; ₂) снова приводит к нормальному распределению N(a; ) с параметрами а = а₁ + а₂ , (складываются математические ожидания и дисперсии).

Наоборот, равномерное распределение устойчивость не обладает.

Пример 2. Найдем закон распределения двух случайных величин, каж­дая из которых распределена по равномерному закону на интервале (0; 1): f₁(x) = 1, если х  (0; 1), и f₁(x) = 0, если х  (0; 1).

Вычисляем интеграл свертки:

.

Здесь подинтегральная функция отлична от нуля (и равна единице) только для условий 0  у  1 и 0  (х – у)  1, которые не выполняются, если х  (0; 2) (иными словами, f₂(x) = 0 для x < 0 или x > 2).

На интервале 0  x  1 приведенные выше условия можно записать как 0  у  x, а на интервале 1  x  2 – как (х – 1)  у  1.

Определяем f₂(x) для 0  x  1:

.

Определяем f₂(x) для 1  x  2:

Записываем выражения f₂(x) по интервалам изменения х:

.

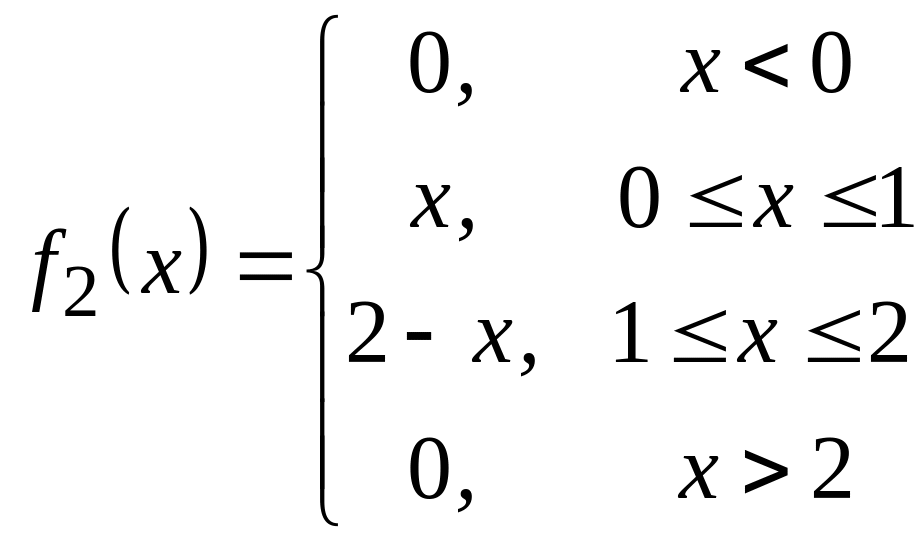Это – треугольный закон распределения Симпсона.

Графики композиций равномерного закона приведены на рис. 7.1 (а).