Лекция 7. Предельные теоремы теории вероятностей

К "предельным теоремам теории вероятности" относят "закон больших чисел" и "центральную предельную теорему". Строго говоря, предельными являются также асимптотические формулы Пуассона и Лапласа, но они формально не относятся к упомянутому выше разделу теории вероятностей.

В доказательстве закона больших чисел и центральной предельной теоремы принимали участие русские математики П.Л. Чебышев и А.М. Ляпунов, может быть поэтому в отечественной научной литературе доказанным теоремам придается слишком большое, чуть ли не мистическое, значение. В действительности же доказывались очевидные вещи, в справедливости которых никто и не сомневался. Правда, у математиков иная система ценностей, в отличие от инженерных наук, где никогда не доказываются утверждения, в справедливости которых уже убедились на основе опытов или правдоподобных рассуждений.

Закон больших чисел

1. Теорема Бернулли. Доказывается, что при увеличении числа однородных независимых испытаний относительная частота появления события А стремится к ее вероятности.

Это предположение изначально лежит в основе универсального метода "статистического определения вероятностей":

.

Для строгого доказательства (очень нужного правоверным математи­кам, которые с точки зрения специалистов–прикладников часто готовы толочь воду в ступе и доказывать очевидные истины), рассмотрим 3-ю форму интегральной теоремы Лапласа:

.

При t = 3 уровень доверия (вероятность выполнения этого условия, гарантия) уже равен Р = 0,997. Если потребуется еще больший уровень доверия, можно принять t = 4, 5, и даже 10. Таким образом, с гаранией, сколь угодно близкой к единице, можно утверждать, что отклонение относительной частоты  ^m/_n  от своего предельного значения р не превысит погрешности , которая стремится к нулю с увеличением n: , .

2. Теорема Чебышева. Доказывается, что с увеличением повторных измерений среднее значение величины приближается к своему математичес­кому ожиданию.

В справедливости этого утверждения также никто не сомневался.

X	x1	x1	x1	…	xk
m	m1	m2	m3	…	mk

Действительно, пусть случайная величина X наблюдается n раз; данные наблюдений сгруппированы, так что известны частоты m_i  появления каждого возможного значения x_i  (m₁ + m₂ + m₃ + … m_k = n). Тогда среднее значение случайной величины по этим n наблюдениям будет равно:

.

Для строгого доказательства рассмотрим неравенство Чебышева, которое мы ранее использовали для обоснования правила "3-х сигм", но сейчас запишем это неравенство для случайного среднего X_cp :

.

При t = 10 гарантия этого утверждения будет больше 0,99; если требуется еще больший уровень доверия, принимаем еще большее значение t.

Таким образом, с гаранией, сколь угодно близкой к единице, можно утверждать, что отклонение среднего от математического ожидания не превысит погрешности, которая стремится к нулю при увеличении n:

, откуда .

Центральная предельная теорема

Давно было замечено, что с увеличением числа слагаемых распределе­ние суммы случайных величин приближается к нормальному.

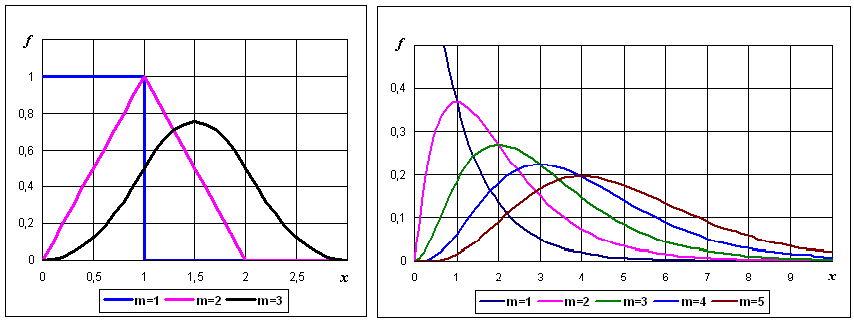
а б

Рис. 7.1. Распределения сумм случайных величин

Так, на рис. 7.1 (а) изображены распределения суммы одного, двух и трех слагаемых (m = 1, 2, 3), каждое из которых имеет ошибку округления до целых значений. Известно, что ошибки округления распределены по равномерному закону на интервале (0; 1). Оказывается сумма двух таких слагаемых имеет ошибку, которая распределена по треугольному закону Симпсона. Распределение ошибки суммы трех слагаемых уже очень похоже на нормальное. Здесь исходное распределение было симметричным, поэтому получилась быстрая сходимость к предельному нормальному виду.

На рис. 7.1 (б) изображены распределения времени работы сложного устройства с учетом резервирования – при выходе элемента из строя он заменяется на запасной (наладчиком или автоматически). Известно, что время работы любого оборудования до первого отказа распределено по экспоненциальному закону. Оказывается, что при резервировании суммарное время работы устройства распределено по законам Эрланга (частный случай гамма-распределения). Распределение времени работы каждого элемента далеко от симметричного, но чем больше в устройстве резервных элементов, тем ближе распределение суммарного времени его работы к нормальному виду. Темп сходимости к предельному симметричному распределению здесь не такой высокий по сравнению с рис. 7.1 (а), но тем не менее считается, что при самых неблагоприятных условиях сумма 10 случайных величин распределена практически нормально.

Распределение Бернулли – это распределение суммы m = X₁ +  X₁ + … + X_n , где X_i – число успехов в одном испытании (0 или 1). Известно, что при увеличении числа испытаний распределение быстро Бернулли приближается к распределению Лапласа (частный случай нормального распределения).

Оценим теперь с точки зрения прикладника теорему, доказанную А.М. Ляпуновым, которая утверждает, что всегда, когда случайная величина является суммой большого количества независимых случайных величин, дисперсия которых мала по сравнению с дисперсией их суммы, эта случайная величина распределена по закону, который приближается к нормальному; данный эффект проявляется, когда наблюдаемые явления определяются влиянием большого количества независимых случайных факторов, вклад каждого из которых в общий процесс очень малый.

У любого нормального человека (не математика) после прочтения текста этой теоремы возникают вопросы. Что такое "большое количество"? Десять – это "большое количество", или еще не очень? Что такое "малая дисперсия"? На сколько она должна быть меньше общей дисперсии? Что значит закон "приближается" к нормальному? Как быстро? Что значит "малый вклад"? Короче, что нового мы узнали по сравнению с уже известными фактами?

На основе центральной предельной теоремы было сформулировано утверждение, которое мы назвали "3-й формой интегральной теоремы нормального закона":

.

Уточняем: это утверждение справедливо при повторении однородных независимых испытаний не менее n = 10 раз; распределение исходной случайной величины х может быть каким угодно.

Кстати, в центральной предельной теореме вовсе не предполагается, что случайные слагаемые должны иметь одинаковое распределение.