Показательный или экспоненциальный закон распределения
По этому закону распределено время работы оборудования до первого отказа. Его дифференциальная функция с точностью до постоянного сомножителя выражается формулой: f(t) = ke–t – для t 0; для t < 0 f(t) = 0.
Сомножитель k находим из условия – площадь под дифференциальной кривой равна единице:
.
Отсюда k = .
Найдем интегральную функцию показательного распределения.
Для t < 0 F(t) = 0;
Для
t 0
.
При вычислении интеграла была сделана замена переменной x = s, dx = ds.
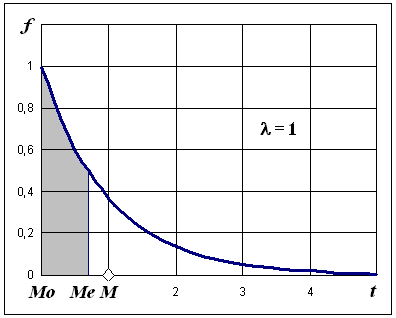
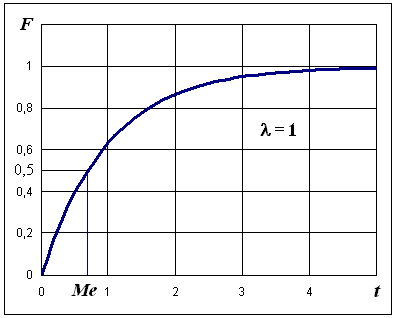
Графики функций этого распределения приведены на рис. 6.6.
|
|
Рис. 6.6. Функции распределения показательного закона для = 1
Вычисляем характеристики показательного распределения.
.
Была сделана замена переменной x = t и применено правило интегрирования по частям; внеинтегральный член оказался равным нулю. Математическое ожидание – это среднее значение случайной величины; здесь M(t) = 1/ = Т – среднее время работы оборудования до первого отказа, центр тяжести фигуры под дифференциальной кривой.
.
.
Наивероятнейшее значение (мода) для показательного распределения равна нулю Мо = 0 (чаще всего оборудование выходит из строя в момент включения).
Интегральная теорема для показательного закона выглядит так:
.
Например:
Р(0 t Т) = e0 – e–T = 1 – e–1 = 1 – 0,368 = 0,632;
Р(T t 2Т) = e–T – e–2T = e–1 – e–2 = 0,368 – 0,135 = 0,233;
Р(2T t 3Т) = e–2T – e–3T = e–2 – e–3 = 0,135 – 0,050 = 0,085;
Р(t > 3Т) = 1 – Р(t 3Т) = 1 – F(3Т) = 1 – (1 – e–3T) = e–3T= e–3 = 0,050.
Здесь учтено, что T = / = 1.
Квантили распределения
Для непрерывной случайной величины в качестве дополнительных характеристик используют, так называемые, квантили, к которым относятся медиана, квартили, децили и процентили.
Квантили делят фигуру под дифференциальной кривой на равновеликие части, или же они делят интервал изменения (варьирования) случайной величины на равновероятные части.
Медиана делит интервал варьирования на две части с вероятностью 50% попадания случайной величины в каждую часть.
Квартили делят интервал варьирования на четыре части с вероятностью 25% попадания случайной величины в каждую часть.
Децили делят интервал варьирования на десять частей с вероятностью 10% попадания случайной величины в каждую часть.
Процентили делят интервал варьирования на сто частей с вероятностью 1% попадания случайной величины в каждую часть.
Обозначения квантилей х , где – вероятность того, что случайная величина примет значение, большие квантиля х : P(x > х) = ( – площадь фигуры плотности вероятности справа от квантиля). Выражение для вероятности противоположного события P(x х) = F(х) = 1 – приводит к вычислительной формуле F(х) = 1 – . Так, для показательного закона медиану Ме = t0,5 находим из равенства F(t0,5) = 1 – 0,5 = 0,5 (см. рис. 6.6). Это значение оказалось равным Ме = ln2. Площадь фигуры под дифференциальной кривой справа от медианы равна 0,5.
Последовательные квартили (нижняя, средняя и верхняя квартили) обозначаются х0,75 < x0,50 < x0,25.
Вопросы для самопроверки
1. Что такое "функция распределения", каковы ее свойства и график, как она называется для дискретной случайной величины?
2. Сформулируйте общую интегральную теорему, приведите ее вариант для непрерывной случайной величины.
3. Что такое "функция плотности вероятности", каковы ее свойства и график?
4. Как связаны между собой функция распределения и функция плотности вероятности?
5. Как вычисляются основные характеристики непрерывной случайной величины?
6. Сформулируйте закон равномерного распределения, опишите область его применения, приведите выражения для дифференциальной и интегральной функций.
7. Опишите характеристики равномерного закона. Выполняется ли для него правило "3-х сигм"?
8. Сформулируйте показательный закон распределения, опишите область его применения, приведите выражения для дифференциальной и интегральной функций.
9. Опишите характеристики показательного закона.
10. Что такое "нормальный закон распределения Гаусса", каковы его характерные особенности?
11. Какие отличия имеются между нормальным распределением и распределением Лапласа?
12. Каковы параметры и и характеристики нормального закона?
13. Сформулируйте три формы интегральной теоремы нормального закона.
14. Какие задачи решаются с помощью 3-й формы интегральной теоремы нормального закона?
15. Что такое "квантили", перечислите их разновидности.
16. Что такое "медиана" и как она рассчитывается?
17. Что такое "квартили" и как они рассчитываются?