Нормальный закон распределения Гаусса

Приложения нормального закона столь обширны, что их невозможно полностью перечислить. Достаточно сказать, что по нормальному закону распределены все размеры животного и растительного мира, рассеяние попаданий при стрельбе, ошибки при изготовлении деталей. Кроме того, при некоторых условиях остальные законы распределения приближаются к нормальному. Так, при увеличении числа испытаний к нормальному закону приближаются распределения Бернулли и Пуассона.

Плотность вероятности и функция распределения нормального закона выражаются через дифференциальную и интегральную функции Лапласа:

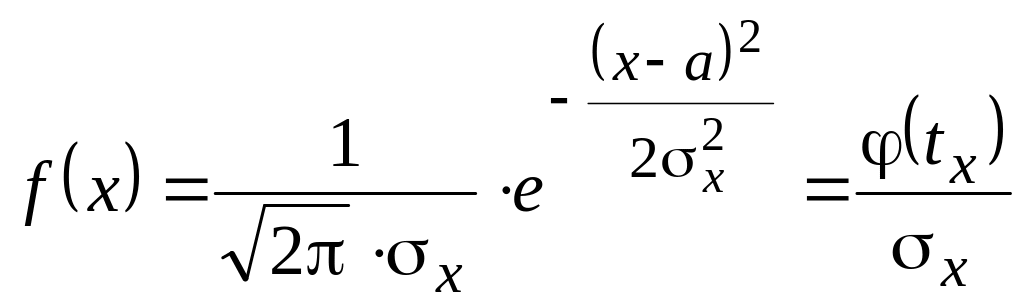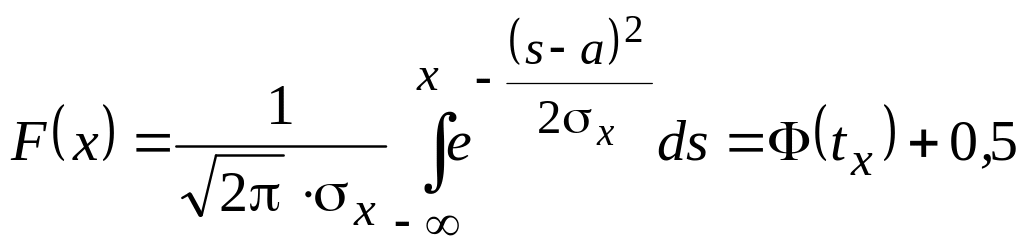, где .

, где .

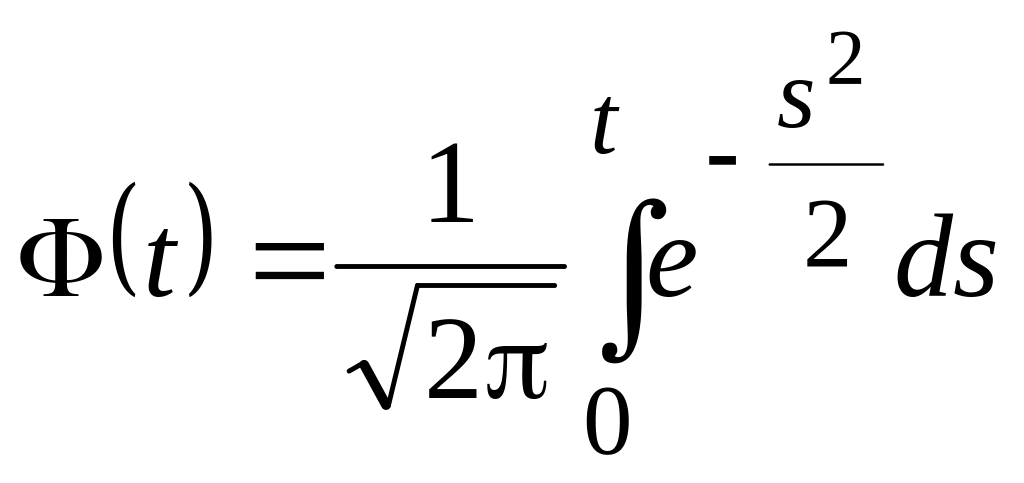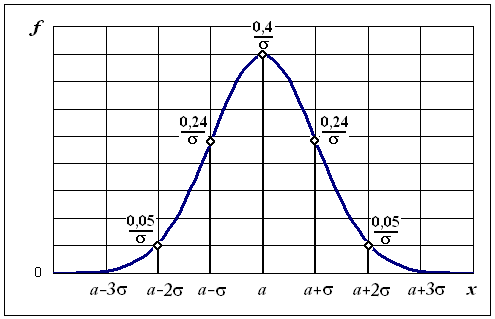
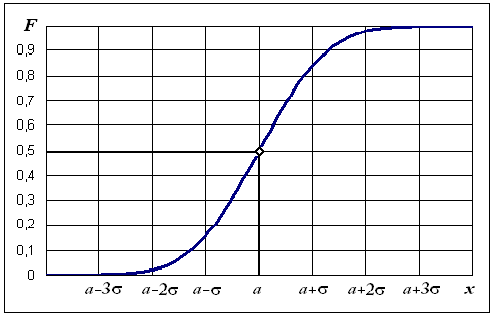
Графики дифференциальной и интегральной функций нормального закона изображены на рис. 6.4.

Рис. 6.4. Графики дифференциальной и интегральной функций нормального закона

Параметры нормального закона а и _х совпадают с его характеристика­ми: а = М(х) – математическое ожидание, _х – стандартное отклонение. Коэффициенты асимметрии и эксцесса для нормального распределения равны нулю.

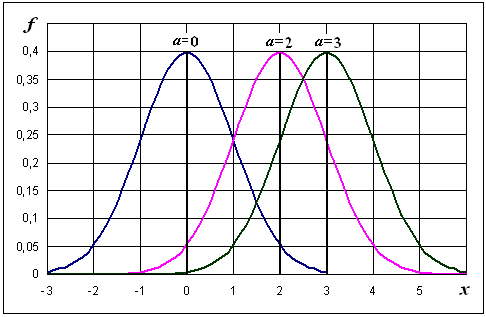
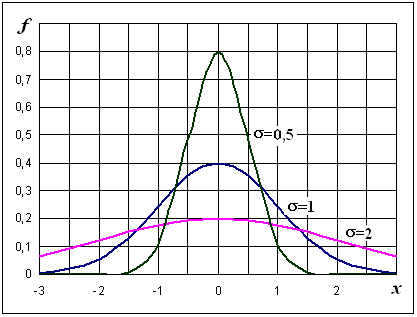
На рис. 6.5 приведены графики плотности вероятности нормального закона при различных значениях параметров.

Рис. 6.5. Зависимость нормального распределения от параметров

Для того, чтобы не произносить стандартной фразы: "Случайная величина х распределена нормально с характеристиками а и _х", договори­лись для этого использовать математическую запись x ~ N(а; _х).

По аналогии с распределением Лапласа сформулируем три формы интегральной теоремы нормального закона.

1. Основная форма – вероятность попадания нормально распределен­ной величины х в заданный интервал с границами х₁ , х₂ :

.

2. Вторая форма предназначена для вычисления вероятности попадания случайной величины в интервал с симметричными границами:

Р(|x – a|  t_x) = 2Ф(t).

3. Утверждение, которое мы называем "третьей формой интегральной теоремы нормального закона" и помещаем здесь для полноты аналогии с тремя формами интегральной теоремы Лапласа, будет доказано немного позже:

.

Здесь фактически записана вторая форма теоремы для случайной величины . В записи третьей формы вместо X_cp традиционно используется . Это не совсем правильно, но допустимо, если понимать, о чем идет речь. Предполагается, что имеется n одинаково распределенных случайных величин X_i , из них составляется среднее – тоже случайная величина – X_cp= (X₁ + X₂ + … + X_n) / n. Утверждается, что эта случайная величина распределена нормально ("центральная предельная теорема") с указанными выше характеристиками. А вот – это одно число, константа, она не имеет изменчивости и потому не может быть как-то распределена. Случайная величина X_cp может быть сгенерирована (датчиком случайных чисел на компьютере) следующим образом, Генерируются первые n значений случайной величины х и из них составляется среднее – первое значение X_cp; следующие n значений х дают нам второе значение X_cp и т.д. Пример: вместо того, чтобы подбрасывать одновременно 10 костей и находить среднее значения выпавших очков, можно подбросить 10 раз одну и ту же игральную кость и вычислить среднее число выпавших очков за 10 бросков.

Найдем основные характеристики X_cp , используя свойства математи­ческого ожидания и дисперсии.

М(X_cp) = М((X₁ + X₂ + … + X_n) / n) = (М(X₁) + М(X₂) + … + М(X_n)) / n = = (а + а + … + а) / n = (nа) / n = а.

D(X_cp) = D((X₁ + X₂ + … + X_n) / n) = (D(X₁) + D(X₂) + … + D(X_n)) / n² = = (D_x + D_x + … + D_x) / n² = (nD_x) / n² = D_x / n.

.

Последнее выражение в нашей литературе называется "ошибкой среднего", а в зарубежной литературе – "стандартной ошибкой".

Как и для 3-й формы интегральной теоремы Лапласа, здесь удобно пользоваться терминологией: P = 2Ф(t) – уровень доверия утверждения о том, что отклонение среднего от математического ожидания не превысит погрешности .

В связи с этим появляется три типовых задачи.

I. Известны параметры распределения а и _х . Дополнительно заданы n и погрешность . Найти уровень доверия Р.

Решение. Из выражения при известных _х , n,  находим t и далее вычисляем P = 2Ф(t).

II. Известны параметры распределения а и _х . Дополнительно заданы n и уровень доверия Р. Найти погрешность .

Решение. Из P = 2Ф(t) по таблицам Лапласа находим t. Далее вычисляем погрешность по формуле .

III. Известны параметры распределения а и _х . Дополнительно заданы уровень доверия Р и погрешность . Найти потребное число n.

Решение. Из P = 2Ф(t) находим t. Далее из формулы при уже известных _х , t,  определяем .

При изучении 3-й формы интегральной теоремы Лапласа была рассмотрена еще одна задача (IV), которая формулируется так: "Известны результаты опыта. Что можно сказать о теоретических характеристиках распределения?" Подобные задачи составляют предмет Математической статистики и будут рассмотрены в соответствующих разделах курса.