Вопросы для самопроверки

1. Сформулируйте задачу Бернулли, приведите ее другие названия.

2. Опишите особенности распределения Бернулли в зависимости от ее параметров.

3. Приведите расчетные формулы для основных характеристик распределения Бернулли.

4. Укажите область применения асимптотических формул Пуассона и Лапласа.

5. Приведите формулу Пуассона и укажите область применения этого распределения. Что такое "реккурентная формула"?

6. Опишите особенности распределения Пуассона в зависимости от параметра.

7. Приведите расчетные формулы для основных характеристик распределения Пуассона.

Лекция 5. Распределение Лапласа

Для n > 30, nр  5, nq  5 распределение Бернулли практически точно аппроксимируется асимптотической формулой Лапласа:

,

где обозначено .

Эта аппроксимация называется "локальной теоремой Лапласа".

На рис. 5.1. для сравнения приведены полигоны распределений Бернулли и Лапласа для р = 0,3; n = 10 и n = 20. Даже для таких небольших значений n соответствие очень хорошее (здесь np = 3 и np = 6) .

Рис. 5.1. Сравнение распределений Бернулли и Лапласа

Функция (t) – затабулирована и называется "дифференциальной функцией Лапласа", или же функцией "стандартизованного нормального распределения Гаусса". Дело в том, что (как выяснилось впоследствии) Лаплас открыл частный случай более общего закона природы, который Гаусс назвал "нормальным". Так получилось, что в русском языке слово "нормальный" имеет совершенно другой смысл, чем для немца Гаусса, но это новое понятие не противоречит сути, поскольку "нормальное распределение" действительно является неким стандартным устойчивым законом природы, к которому при определенных условиях приближаются другие законы распределения.

Ф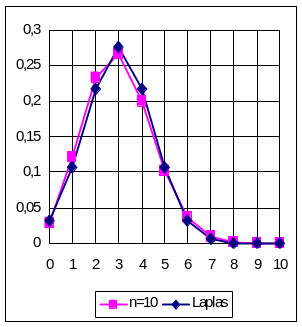 ункция (t) имеет некоторые особенности, которые учтены при составлении таблиц. Во-первых, эта функция – четная, (график ее симметричен относительно оси ординат), поэтому таблицы составлены только для неотрицательных значений t; для отрицательных t используется соотношение четности (–t) = (t). Во-вторых, функция – неотрицательна и имеет горизонтальную асимптоту – ось абсцисс; иными словами, при увеличении t значения (t) приближаются к нулю, поэтому таблицы составлены только до значений t  5; так: (3) = 0,00443; (4) = 0,00013; (5) = 0,00001; для боль­ших значений аргумента (t)  0. Максимальное значение функции дости­гается при t =0 и равно (0) = 0,3989. Характерные особенности дифферен­циальной функции Лапласа изображены на рис. 5.2.

И нтегральная теорема Лапласа

Для больших n вычисление вероятностей отдельных значений m лишено особого смысла, т.к. даже для самого вероятного значения – моды получается – очень малое число при большом n.

В практических задачах для больших n требуется находить вероятности попадания случайной величины в некоторые интервалы P(m₁  m  m₂), т.е. вычислять вероятности не одного значения m, а вероятности всех целых значений m из интервала [m₁ , m₂]: .

Рассмотрим приращение t_m при увеличении m на единицу:

.

Оказывается, .

Лаплас ввел и затабулировал функцию , которая называется "интегральной функцией Лапласа".

Теперь вероятность попадания случайной величины m в интервал [m₁ , m₂] можно записать, как разность значений интегральной функции Лапласа на краях этого интервала: .

Это утверждение называется "интегральной теоремой Лапласа".

Ф ункция Ф(t) имеет некоторые особенности, которые учтены при составлении таблиц. Во-первых, эта функция – нечетная, (график ее центрально симметричен относительно начала ординат), поэтому таблицы составлены только для неотрицательных значений t; для отрицательных t используется соотношение нечетности Ф(–t) = –Ф(t). Во-вторых, функция Ф(t) – возрастающая и имеет горизонтальные асимптоты – Ф_min = –0,5 и Ф_max = 0,5; иными словами, при увеличении t значения Ф(t) приближаются к 0,5, поэтому таблицы составлены только до значений t  5; так: Ф(3) = 0,49865; Ф(4) = 0,49997; Ф(5) = 0,5000; для еще больших значений аргумента Ф(t) = 0,5. Значение функции при t =0 равно нулю Ф(0) = 0. Характерные особенности интегральной функции Лапласа изображе­ны на рис. 5.3.