Биномиальные коэффициенты

(n =1)							1		1
(n =2)						1		2		2
(n =3)					1		3		3		1
(n =4)				1		4		6		4		1
(n =5)			1		5		10		10		5		1
(n =6)		1		6		15		20		15		6		1
(n =7)	1		7		21		35		35		21		7		1

Здесь каждый коэффициент равен сумме двух соседних с ним коэффициентов предыдущего ряда.

Для вычисления математического ожидания и дисперсии требуется суммировать следующие выражения:

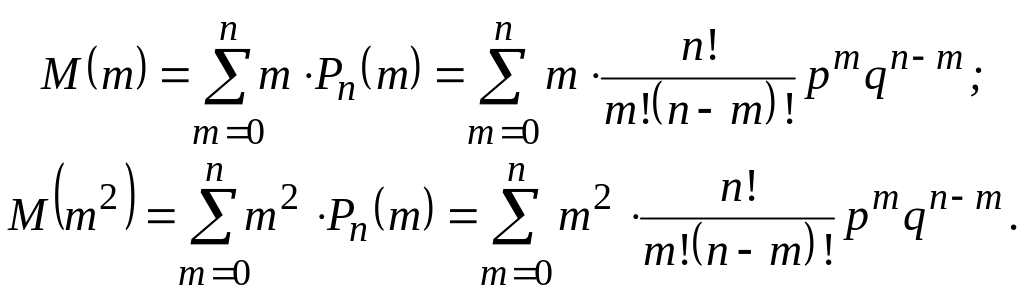
Можно предложить студентам найти способ вычисления сумм M(m), M(m(m–1)), M(m(m–1)(m–2)), но мы вычислим все суммы окольным путем с помощью доказанных ранее свойств математического ожидания и дисперсии.

Напоминаем, что рассматривается задача о повторении однородных независимых испытаний, в каждом из которых случайная величина X_i (число успехов в одном испытании) может принимать только два значения: 0 или 1.

Xi	0	1
Вер.	q	p

Определяем первые три момента распределения для одного испытания: m₁ = 0q + 1p = p, m₂ = 0²q + 1²p = p, m₃ = 0³q + 1³p = p; откуда M(X_i) = m₁ = p, D(X_i) = m₂ – (m₁)² = p – p² = pq,  ₃(X_i) = m₃ – 3m₁m₂ +2(m₁)³ = pq(q – p).

Общее число успехов при n  испытаний равно сумме X = X₁ + X₂ + … + X_n . Известно, что математическое ожидание суммы случайных величин равно сумме математических ожиданий, дисперсия суммы независимых случайных величин также равна сумме дисперсий, можно показать, что для независимых случайных величин такое же свойство имеет место и для момента 3-го порядка.

Отсюда сразу получаем: M(m) = np, D(m) = npq, ₃(m) = npq(q – p).

.

Можно еще доказать двойное неравенство, однозначно устанавливаю­щее местоположение моды (наивероятнейшего числа успехов при n испытаниях): np – q  Mo  np + p. На интервале длиной (np + p) – (np – q) = = p + q = 1 может быть только одно целое Mo, или же два соседних, если целочисленны края интервала. Предлагается студенту в качестве полезного упражнения самостоятельно вывести это двойное неравенство. Указание: надо в неравенство P_n(Mo–1)  P_n(Mo)  P_n(Mo+1) подставить выражения для P_n(m) и сократить общие множители.

Для примера решим типичную задачу на распределение Бернулли.

Вероятность того, что электротехничный прибор потребует ремонта в гарантийный срок, равна 0,25. Найти вероятность того, что на протяжении гарантийного срока из семи приборов ремонта потребуют m = 0, 1, 2, ... приборов; потребуют ремонта не более четырех, не меньше двух, больше двух и меньше шести приборов.

Решение. Речь идет о повторении однородных независимых испытаний (т.к. p = 0,25 = Const). Число испытаний (число приборов) равно n = 7 (n < 30), поэтому применяем формулу Бернулли.

.

В этой задаче p = 0,25; q = 1 – p = 0,75; биномиальные коэффициенты можно определить также по треугольнику Паскаля.

Для m = 0, 1, 2, ..., 7 расчеты удобно свести в таблицу, в последнем столбце которой приведены накопленные суммы вероятностей (значения кумуляты) F(m). Напоминаем, что функция распределения (кумулята) определена как F(m) = P(X  m), поэтому F(0) = P_n(0) = 0,133484.

m	Cnm	pm	qn–m	Pn(m)	F(m)
0	1	1	0,133484	0,133484	0,133484
1	7	0,25	0,177979	0,311462	0,444946
2	21	0,0625	0,237305	0,311462	0,756409
3	35	0,015625	0,316406	0,173035	0,929443
4	35	0,003906	0,421875	0,057678	0,987122
5	21	0,000977	0,5625	0,011536	0,998657
6	7	0,000244	0,75	0,001282	0,999939
7	1	0,000061	1	0,000061	1,000000

С помощью кумуляты вероятность попадания случайной величины в полуоткрытый интервал m₁ < m  m₂ вычисляется как разность значений функции F(m) на краях этого интервала: P(m₁  m  m₂) = F(m₂) – F(m₁–1). Вычисляем: P(m  4) = F(4) = 0,9871; P(m  2) = P(2  m  7) = F(7) – F(1) = = 1 – 0,4450 = 0,5551; P(2<m<6) = P(3m5) = F(5) – F(2) = 0,9987 ‑ 0,7564 = 0,2422.

Заметим, что во многих учебниках функция F(x) определена немного по-другому: F(x) = P(X < x). Тогда для нашего примера надо было бы при­нять F(0) = 0 и изменить формулу расчета вероятности попадання случайной величины в полуоткрытый интервал: P(m₁  m < m₂) = F(m₂) – F(m₁) или же P(m₁  m  m₂) = F(m₂+1) – F(m₁). Оба определения функции F(x) эквивалент­ны, но надо придерживаться одного стандарта.

Вычисляем характеристики распределения Бернулли:

M(m) = np = 70,25 = 1,75; D(m) = npq = 70,250,75 = 1,3125; ; M(m) – q  Mo  M(m) + p; 1,75 – 0,75  Mo  1,75 + 0,25; 1  Mo  2; P(1) = P(2) = P_max .

Согласно правилу "трех сигм" вероятные значения m не превышают M(m) + 3_m = 1,75 + 31,146 = 5,19  5.

Ниже приведен полигон распределения Бернулли для данного примера:

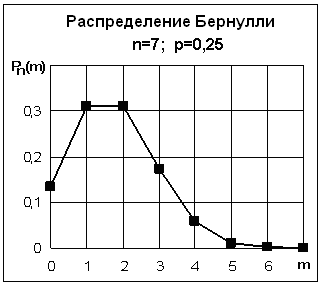
Рис. 4.3. Полигон распределения Бернулли