Свойства дисперсии

1. Дисперсия постоянной равна нулю.

Действительно, т.к. М(С) = С, то D(C) = M(C – C)² = M(0) = 0.

2. При вынесении постоянного множителя за знак дисперсии его надо возводить в квадрат:

D(kx) = M(kx – ka)² = M(k²(x – a)²) = k²M(x – a)² = k²D(x).

3. Дисперсия суммы независимых случайных величин равна сумме их дисперсий D(x + y) = D(x) + D(y). Здесь важна оговорка о "независимости" величин. При невыполнении этого условия данное свойство не имеет места. Например, при у = х дисперсия суммы не равна сумме дисперсий D(x + х) = D(2x) = 4D(х)  D(х) + D(х).

4. Дисперсия суммы двух случайных величин равна сумме их дисперсий и удвоенной ковариации, где ковариация – смешанный централь­ный момент _xy – математическое ожидание произведения отклонений случайных величин от своих центров: _xy = М(х – a)(y – b), где a = M(x), b = M(y). Если обозначить дисперсии и ковариацию _xx , _yy , _xy  (эквивалентные обозначения), то утверждается, что D(x + y) = _xx + _yy + 2_xy .

Доказательство:  D(x + у) = М((x + y) – (а + b))² = М((x – а) + (у – b))² = = М(x – а)² + М(у – b)² + 2М(x – а)(у – b) = _xx + _хх + 2_xх .

Для независимых случайных величин М(х – a)(y – b) = М(х – a)М(y – b) (согласно 4-му свойству математического ожидания), М(х – a) = М(y – b) = 0 (центральное свойство математического ожидания), следовательно, для независимых случайных величин ковариация равна нулю _xy = 0. В этом случае справедливо утверждение D(x + y) = D(x) + D(y).

В другом частном случае у = х (зависимые величины) ковариация равна дисперсии _xy = _xx  и опять получается правильный ответ, который согласуется с правилом вынесения постоянного множителя за знак дисперсии: D(x + х) = _xx + _хх + 2_xх = 4_xx = 4D(х).

Следствие: Для независимых случайных величин

D(x + у) = ² D(x) + ² D(y).

Например, D(x – у) = D(x) + D(у); (здесь  = –1, ² = 1).

Правило "3-х сигм"

Интересно, что для любой случайной величины справедливо следующее практическое правило: "Случайные отклонения от центра распределения – маловероятны". На практике это означает, что все данные с отклонениями, большими 3_х , считаются неслучайными, чаще всего – выбросами, грубыми ошибками в записи чисел, или же поясняются неоднородностью совокупности (эти сомнительные данные с большими отклонениями очевидно не принадлежат изучаемой совокупности).

Оценим вероятность появления больших отклонений (выведем неравенство Чебышева). Запишем и преобразуем формулу для дисперсии:

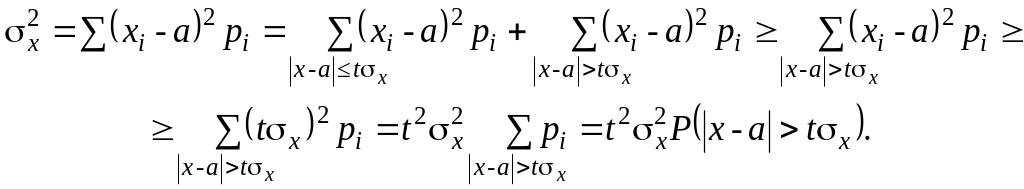
Отсюда получаем довольно грубую оценку вероятности появления больших отклонений

и вероятности противоположного события

.

Если t = 3, то Р(|x – a|  3_x) > 1 – ¹/₉ > 0,89.

Таким образом, с уровнем доверия не менее 90% можно утверждать, что случайные отклонения |x – a| не превышают 3_x .

m	P(m)	F(m)
1	0,3000	0,3000
2	0,2100	0,5100
3	0,1470	0,6570
4	0,1029	0,7599
5	0,0720	0,8319
6	0,0504	0,8824
7	0,0353	0,9176
8	0,0247	0,9424
9	0,0173	0,9596
10	0,0121	0,9718
11	0,0085	0,9802
12	0,0059	0,9862
13	0,0042	0,9903
14	0,0029	0,9932
15	0,0020	0,9953
16	0,0014	0,9967
17	0,0010	0,9977
18	0,0007	0,9984
19	0,0005	0,9989
20	0,0003	0,9992

В заключение темы "Дискретная случайная величина" рассмотрим интересную функцию, которая будет основной в определении непрерывной случайной величины, а именно "кумуляту" – функцию накопленных вероятностей. Для примера в таблице справа приведен закон распределения X – числа испытаний m до первого успеха для р = 0,3 (q = 0,7). Вероятности P(m) здесь убывают по геометрической прогрессии P(m) = pq^m–1 . В последней колонке таблицы вычислены накоплен­ные суммы вероятностей ; в общем случае эта функция определяется как F(m) = P(X  m). Знание кумуляты позволяет легко находить вероятности попадания случайной величины в заданные интервалы по формуле: P(m₁ < m  m₂) = F(m₂) – F(m₁). Например, Р(2 m 8) = Р(1< m 8) = = F(8) ‑ F(1) = 0,9424 – 0,3000 = 0,6224. Этот способ значительно проще непосредственного суммирования вероятностей:

Р(2 m 8) = P(2) + P(3) + P(4) + P(5) + P(6) + P(7) + P(8) = = 0,2100 + 0,1470 + 0,1029 + + 0,0720 + 0,0504 + 0,0353 + 0,0247 = 0,6424.

Для непрерывной случайной величины функция F(x) называется "функцией распределения" или "интегральной функцией распределения". Она определена для всех значений х, в том числе и между узлами дискретной случайной величины. Согласно определению F(х) = P(X  х), на интервалах [x_i , x_i+1) кумулята сохраняет постоянные значения, равные F(x_i); F(х < х₁) = 0; F(х  х_k) = 1 (здесь х_k – наибольшее значение случайной величины).

График кумуляты (функции распределения для дискретной величины) – ступенчатый, значения кумуляты изменяются скачками в заданных узлах x_i случайной величины от 0 до 1.