11.2. Ряд фур"є за тригонометричною системою функцій

Нехай дано тригонометричну систему функцій

. ( 7 )

Всі функції цієї системи – періодичні з спільним періодом .

■Взявши замість x, отримаємо, наприклад, для косинуса

. ■

Теорема 1. Тригонометрична система функцій (7) ортогональна на відрізку і на довільному відрізку довжини .

■Достатньо довести теорему для відрізка . Доведімо, що

для будь-яких n, ( 8 )

для різних m і n, ( 9 )

для будь-яких m і n, ( 10 )

і, крім того,

( 11 )

Але

,

звідки ми отримуємо рівності (8) і (після перетворення добутків тригонометричних функцій в алгебричні суми) – рівності (9) - (10). Перша з формул (11) є очевидною, для отримання інших достатньо застосувати формули зниження степеня. Наприклад,

.■

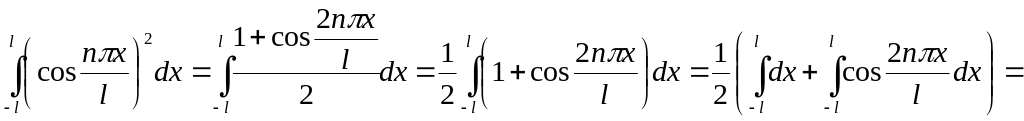
Встановимо тепер відповідність між довільною функцією і рядом Фур"є для неї за тригонометричною системою (7). Маємо

 , ( 12 )

де на підставі формул (5)

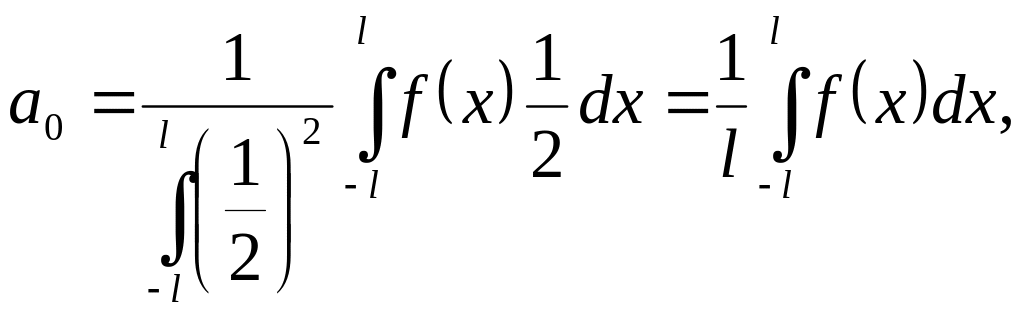
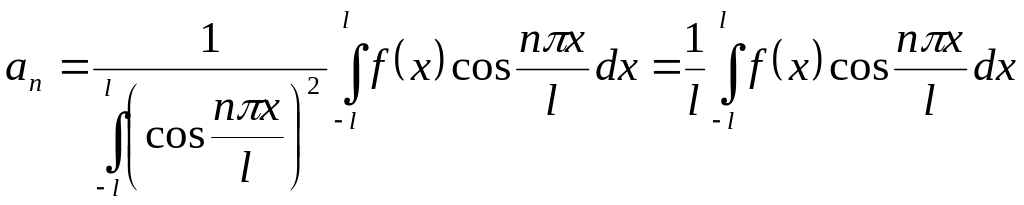
і аналогічно

.

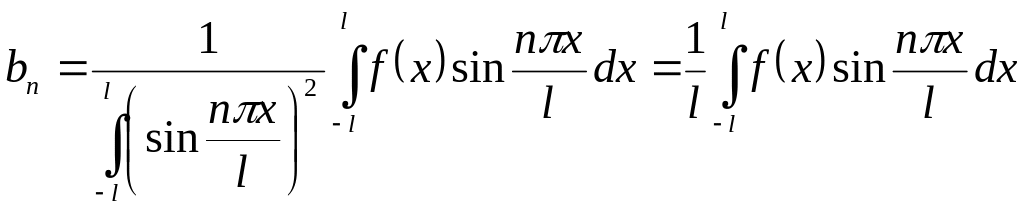Таким чином,

. ( 13 )

Зауваження 1. Сума ряду (12) є періодичною функцією з періодом 2l

(інакше кажучи, є 2l-періодичною). Отже, якщо якась функція розвивається в ряд Фур"є (12), (13) на множині всіх дійсних чисел, вона повинна бути 2l-періодичною.

Означення 3. Функція називається кусково-монотонною на відрізку , якщо відрізок можна розбити на скінченну кількість частин (підінтервалів), на кожній з яких функція є монотонною.

Теорема 2 (теорема розвивності Діріхле¹). Якщо 2l-періодична функція обмежена і кусково-монотонна на відрізку , то її ряд Фур"є (12), (13) збігається в будь-якій точці x. Сума ряду дорівнює самій функції

( 14 )

в кожній точці x неперервності функції. Якщо ж є точкою розриву функції, то сума ряду Фур"є в ній дорівнює півсумі лівої і правої границь функції в цій точці,

( 15 )

де .

Отже,

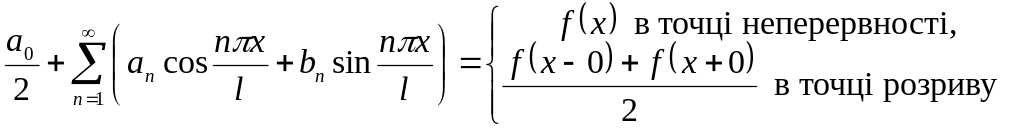(16)

(якщо коефіцієнти ряду визначаються формулами (13)).

Зауваження 2. Можна довести, что для парної або непарної функції формула (13) для коефіцієнтів Фур"є і сам ряд Фур"є набувають іншого вигляду. Саме,

для парної функції маємо

, ( 17 )

і її ряд Фур"є містить тільки косинуси,

 ;

для непарної функції маємо

, ( 18 )

і її ряд Фур"є містить тільки синуси,

 .

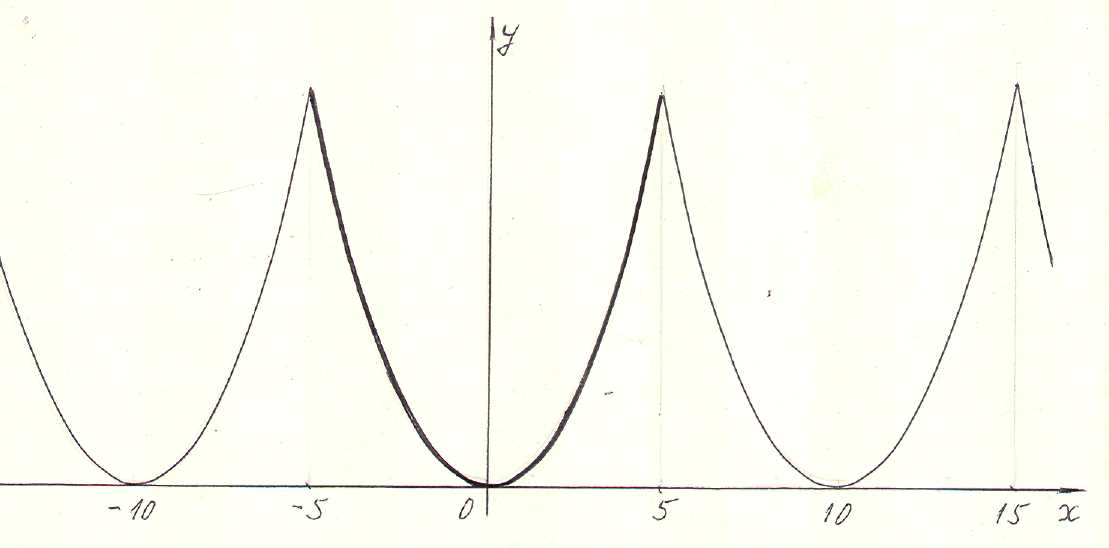Приклад 1. Функцію задано формулою

на відрізку . Развинути її в ряд Фур"є. Рис. 1 Розглянемо -періодичну функцію ¹, яка визначена даною функцією на відрізку (див. рис. 1). Їй відповідає ряд Фур"є (12), (13) (для випадку , тобто ), саме

 .

Функція є парною, тому ми знаходимо коефіцієнти Фур"є у вигляді (17),

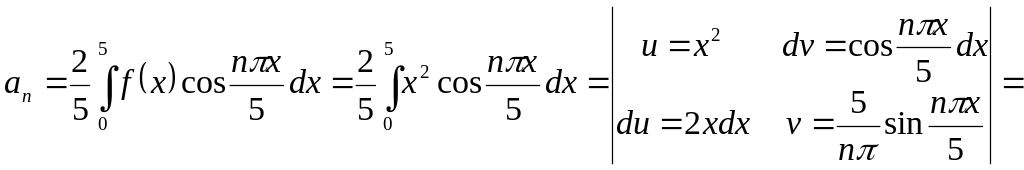
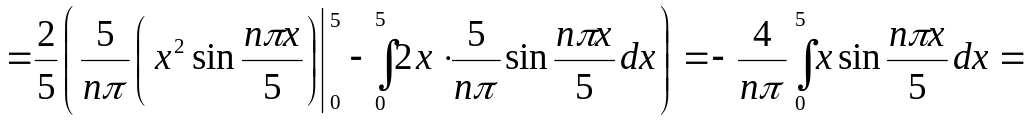
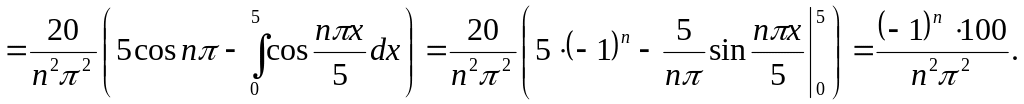
Функція задовольняє умови теореми розвивності Діріхле: вона обмежена і кусково-монотонна на ( , спадає на підінтервалі і зростає на підінтервалі ). Крім того, вона неперервна на множині всіх дійсних чисел, і тому її ряд Фур"є збігається до неї в будь-якій точці. Зокрема, він збігається до функції на відрізку . Таким чином,

Приклад 2. Функцію задано формулою

на інтервалі . Розвинути її в ряд Фур"є.

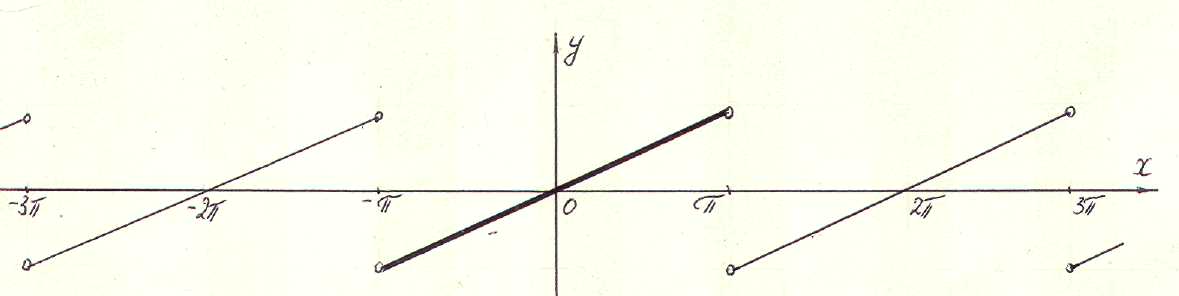Розглянемо -періодичну функцію , яка визначена Рис. 2 даною функцією на інтервалі (див. рис. 2)¹. Їй відповідає ряд Фур"є (для випадку , тобто для випадку )

 .

Функція непарна, і ми знаходимо для неї коефіцієнти Фур"є за формулою (18),

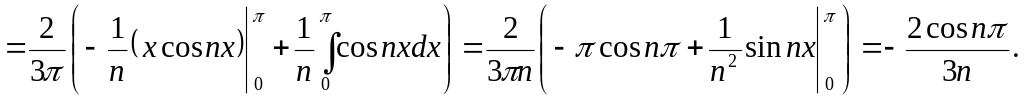
Функція задовольняє всі умови теореми Діріхле (вона обмежена числами і зростає на інтервалі ) і є неперервною на множині всіх дійсних чисел, за виключенням точок 0, . Тому її ряд Фур"є збігається до функції в усіх точках, крім названих. Зокрема, він збігається до функції на заданому інтервалі , тобто

Сума ряду Фур"є в точках дорівнює 0. Для точки ми міркуємо наступним чином:

аналогічно для іншої точки

Приклад 3. Нехай задано функцію

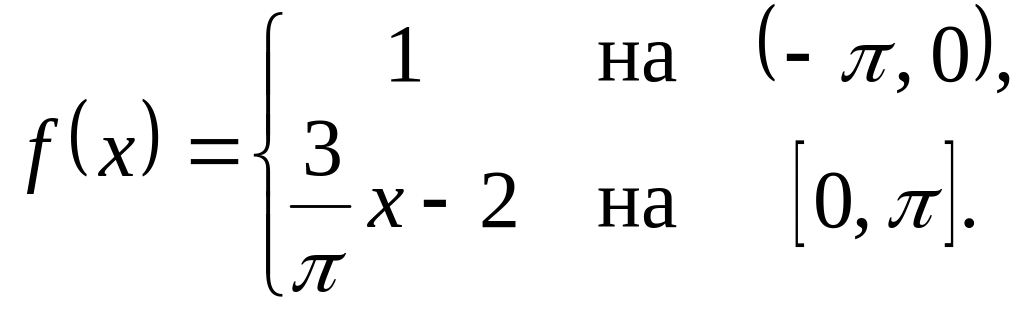
Розвинути її в ряд Фур"є.

Рис. 3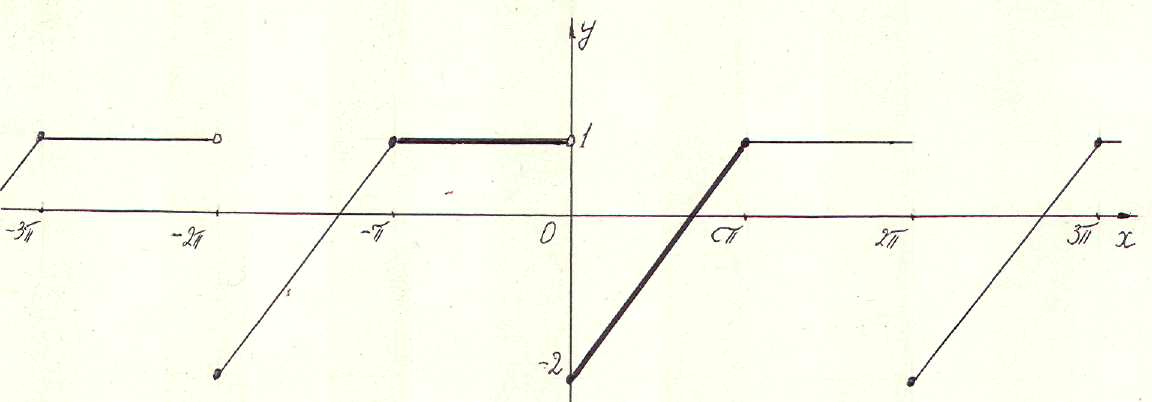

Розглянемо -періодичну функцію , визначену на інтервалі даною формулою (рис. 3). Відповідний їй ряд Фур"є (12), (13) (для випадку , тобто для випадку )



де

.

Функцію задано різнтми виразами на інтервалах , , і тому ми повінні обчислювати інтеґрали по як суми інтеґралів по інтервалах и .

;

.

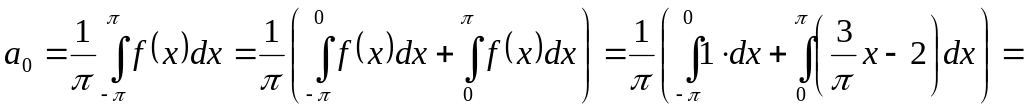
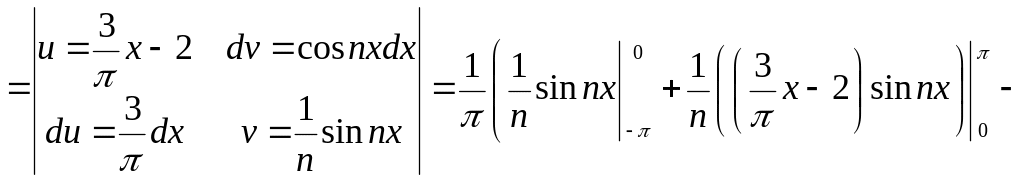
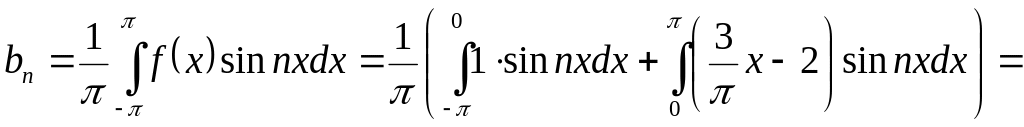
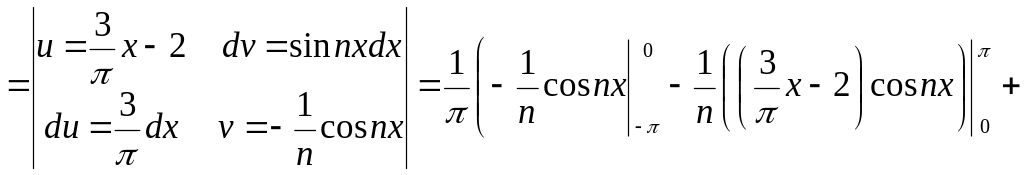
Функція задовольняє умови теореми Діріхле (вона обмежена знизу і зверху числами -2 и 1, є сталою на відрізку і зростаючою на відрізку ). Крім того, вона неперервна на множині всіх дійсних чисел, за винятком точок . Ряд Фур"є для функції збігається до неї в будь-якій точці, відмінній від названих. Зокрема, він збігається до даної функції на об"єднанні інтервалів і , тобто

.

Значення суми ряду Фур"є в точці розриву x=0 дорівнює

.

Воно не збігається з значеннямм функції в цій точці.