9.3.2. Абсолютно і умовно збіжні ряди

Нехай дано ряд з довільними дійсними членами

. ( 33 )

Введімо ряд з абсолютних величин його членів, тобто ряд

( 34 )

Теорема 12. Якщо ряд (34) з абсолютних величин членів ряду (33) збігається, то ряд (33) також збігається.

■Нехай

- n-а частова сума ряду (34). На підставі його збіжності існує границя

,

і

для будь-якого n. Подамо тепер n-у часткову суму ряду (33) в такому вигля-ді:

,

де - сума всіх додатних доданків ряду (33) в , а - сума абсолютних величин від"ємних доданків. Очевидно,

.

Це означає, що суми обмежені зверху числом і тому мають границі при ,

.

Отже, існує границя S n-ої часткової суми ряду (33),

,

тобто ряд збігається.■

Означення 8. Якщо ряд (34) з абсолютних величин членів ряду (33) збігається, то ряд (33) називається абсолютно збіжним (кажуть, що він абсолютно збігається).

На підставі означення 8 ми можемо назвати теорему 12 теоремою про абсолютну збіжність ряду з довільними дійсними членами.

Наслідок. З доведення теореми 12 випливає, що в абсолютно збіжному ряді збігаються ряди з додатних і від"ємних членів (відповідно до і ).

Приклад 29. Ряд

абсолютно збігається, оскільки ряд з абсолютних величин його членів, тобто ряд

,

є збіжним гармонічним рядом (8) з .

Означення 9. Якщо ряд (33) з довільними дійсними членами збігається, але ряд з абсолютних величин його членів розбігається, ряд (33) називається умовно збіжним (кажуть, що він умовно збігається).

Зауваження 2. На підставі доведення теореми 12 ми можемо зробити висновок, що в умовно збіжному ряді обидва ряди - з додатних і від"ємних членів - розбігаються.

Приклад 30. Ряд

(див. приклад 26) збігається умовно, оскільки ряд з абсолютних величин його членів, тобто ряд

,

розбігається, як гармонічний з .

Для встановлення абсолютної збіжності ряду (33) з довільними дійсними членами ми можемо застосовувати всі ознаки з п. 9.2. Розглянемо кілька випадків.

9.3.3. Деякі ознаки абсолютної збіжності

1. Якщо існує збіжний ряд з додатними членами

( 35 )

такий, що

( 36 )

(принаймні для достатньо великих n), то ряд (33) абсолютно збігається.

Приклад 31. Ряд

абсолютно збігається для будь-яких значень x, бо ряд з абсолютних величин його членів

збігається для всіх x на підставі першої ознаки порівняння:

для всіх x і , а ряд з додатних членів

збігається, як гармонічний з .

Зауваження 3. Якщо для деякого розбіжного ряду з додатними членами

виконується нерівність

(принаймні для достатньо великих n), то ряд (33) не може збігатися абсолютно. Але це не означає розбіжності самого ряду: він може збігатися умовно.

2. Якщо для ряду (33) з дійсними членами існує границя

, ( 37 )

то ряд абсолютно збігається при і розбігається при .

■Границя (37) виражає достатню ознаку збіжності Даламбера для ряду (34) з абсолютных величин членів ряду (33). У випадку розбігається не тілько ряд (34), але й ряд (33), оскільки для нього не виконується необхідна умова збіжності числового ряду. Див. теорему 8.■

Приклад 32. Нехай дано функціональний ряд

,

тобто ряд, членами якого є функції. Треба дослідити, для яких значнь x він збігається.

Означення 9. Множина всіх значень x, для яких функціональний ряд збігається, називається областю його збіжності.

На підставі означення 8 ми повинні знайти область збіжності ряду прикладу 32.

Загальний член ряду є функцією від x, яку ми позначимо ,

.

Для фіксованого значення x ознака Даламбера для ряду з абсолютних величин членів даного ряду дає

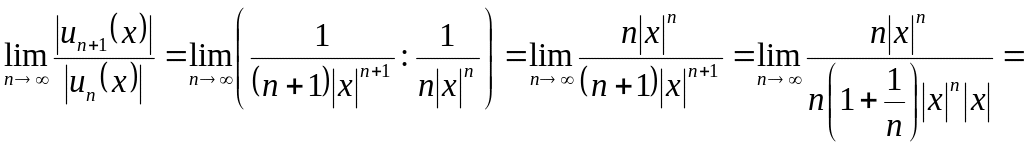
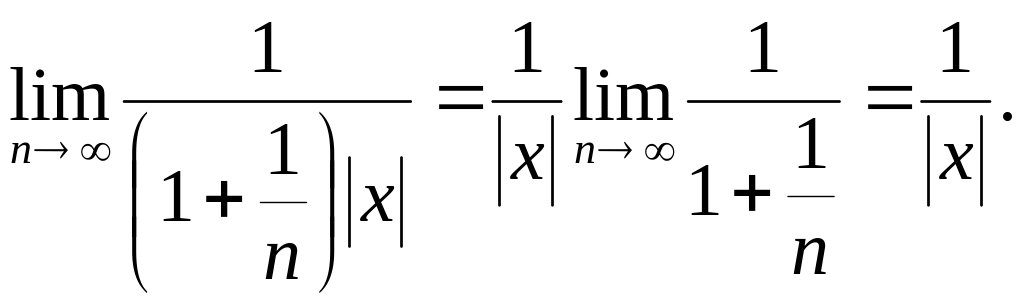
Ряд абсолютно збігається, якщо отримана границя менше 1, тобто якщо

;

ряд розбігається, якщо

.

Залишається дослідити поведінку ряду в двох точках .

В точці ряд набуває вигляду

і розбігається, як гармонічний з . В точці ряд має вигляд

і збігається за ознакою Лейбніца (див. Приклад 26).

Таким чином, ряд збігається для . Інакше кажучи, його областю збіжності є множина точок , тобто об"єднання двох інтервалів і .

Приклад 33. Доведіть самостійно, що областю збіжності функціонального ряду

є множина .

Приклад 34. Знайти область збіжності ряду

.

Ров"язання. n-ий, (n + 1)-ий члени ряду та їх абсолютні величины відповідно дорівнюють

.

На підставі ознаки Даламбера для ряду з абсолютних величин (для фіксованого x)

.

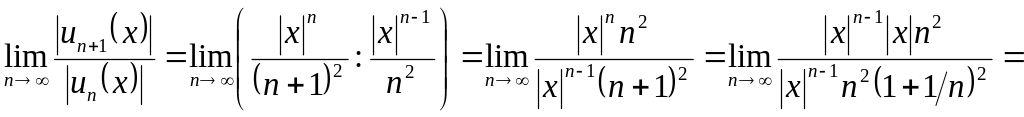
Ряд абсолютно збігається, якщо , тобто якщо .

Ряд розбігається, якщо , тобто .

Необхідно дослідити випадок

Для ми маємо ряд

,

який збігається за ознакою Лейбніца.

Для відповідний ряд

збігається, як гармонічний з .

Відповідь: областю збіжності ряду є відрізок .

Приклад 35. Та ж сама задача для функціонального ряду

Відповідь: .

Приклад 36. Знайти область збіжності ряду

.

Тут

,

і для фіксованого x за ознакою Даламбера для ряду з абсолютних величин

.

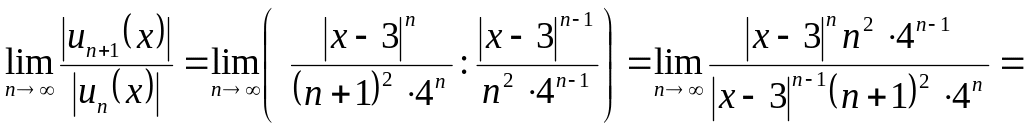
Ряд абсолютно збігається, якщо

,

і розбігається, якщо

.

Таким чином, ми знаєм поведінку ряду в усіх точках, за винятком точок .

Для ряд набуває вигляду

і збігається, як гармонічний з .

Для ряд має вигляд

і абсолютно збігається (його збіжність, але не абсолютна, випливає також з оз-наки Лейбніца).

Отже, областю збіжності ряду є відрізок . Останній має довжину 8 і центр і може бути поданим у вигляді .