Обратная интерполяция
Постановка задачи: по таблице функции определить x, соответствующее заданному y.
Решение поставленной задачи можно осуществить различными способами.
Способ 1. Применение метода итераций к 1-й интерполяционной формуле Ньютона.
(Способ является актуальным при ) .
.
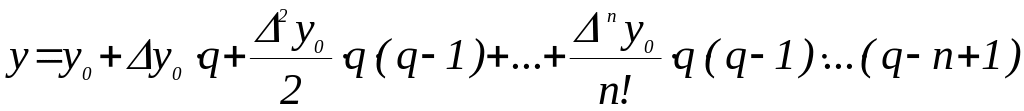Данный полином необходимо преобразовать к виду
,
причем
.
К полученному выражению применяется метод итераций
.
Итерационный
процесс прекращается, когда
и для дальнейших вычислений используется
последнее приближение
.
Завершающим этапом является непосредственное определение искомого значения:
,
где
.
Пример.
Функция
задана таблично(табл. 3 .5). Необходимо
найти
,
при котором
10,618
.
Таблица 3.5
|
|
|
|
2 |
10,4 |
|
|
|
|
2 |
|
3 |
12,4 |
|
-0,4 |
|
|
1,6 |
|
4 |
14,0 |
|
|
.
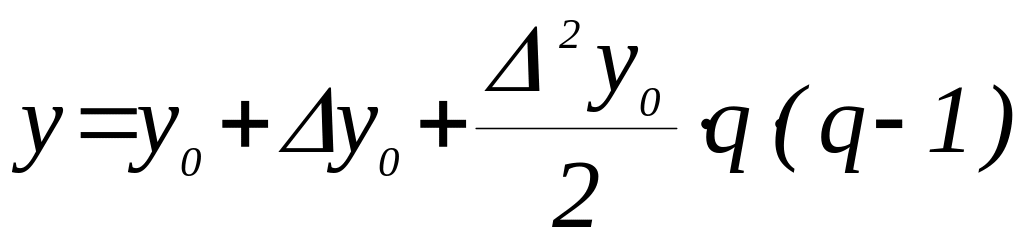После эквивалентных преобразований
.
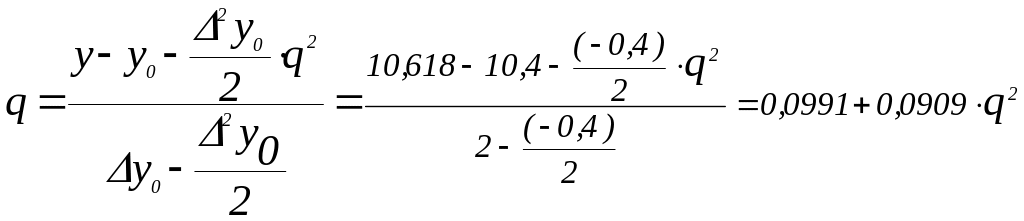0,0991
,
0,0991+0,0909
0,09912
0,1
.
Если
0,001,
то итерационный процесс прекращается.
x = x0+q h+0,11=2,1.
Способ 2 . Применение интерполяционного полинома в форме Лагранжа .
(Способ является актуальным при ) .
Если
считать
,
то
.
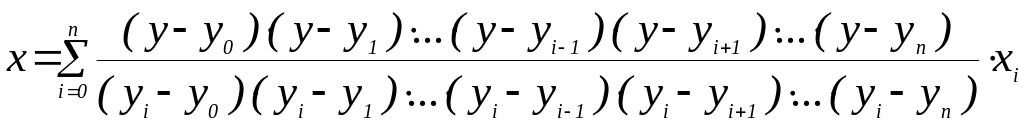Оценка погрешности приближения функции интерполяционным полиномом
При
интерполяции происходит замена исходной
функции
полиномом
.
В узлах интерполяции выполняется равенство .
Необходимо
оценить погрешность приближения в
других точках
,
где
-
остаточный член (см. рис. 3.4).
Д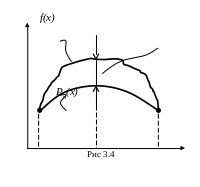
ля
определения
на
накладывается дополнительное
ограничение :
в рассматриваемой области
,
содержащей узлы интерполяции
( i
= 0,1,…,n
),
должна
иметь производные
, ,
.
•
•
•
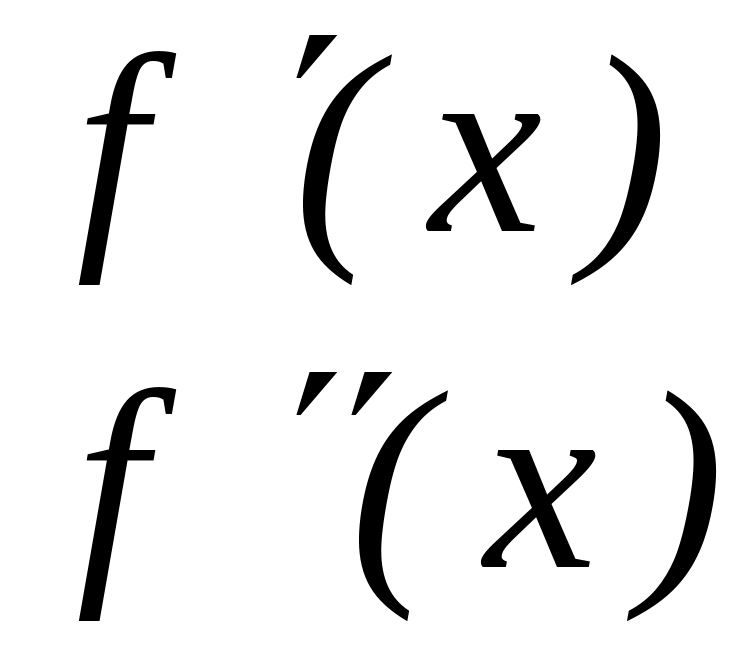
Зафиксируем
.
Рассмотрим вспомогательную функцию
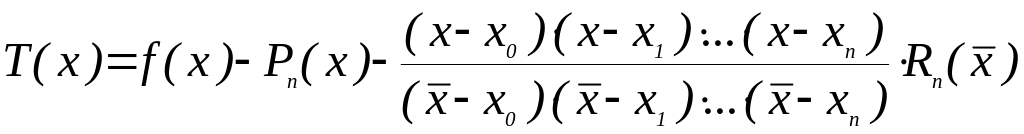
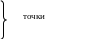
при
.
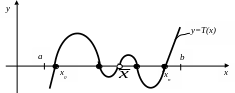
Рис. 3.5
Дополнительная информация
Т
еорема
Ролля ( для
частного случая ) .
Если на : 1) непрерывна,
2) дифференцируема,
3)
,
т
о
существует минимум одно значение
,
для которого
.
По теореме Ролля
минимум в n+1
точках.
минимум в n
точках.
• •
• •
• •
минимум
в 1 точке.
Обозначим
эту точку через
и
вычислим
.
Т.к. 
и
,
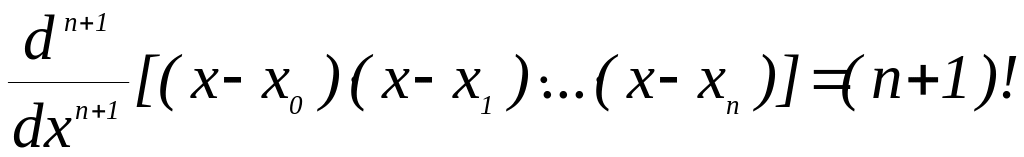то при
.
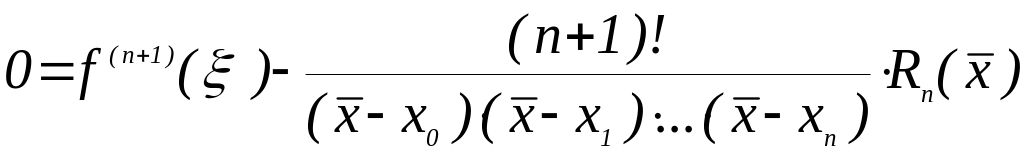Т.к. - произвольное, то
,
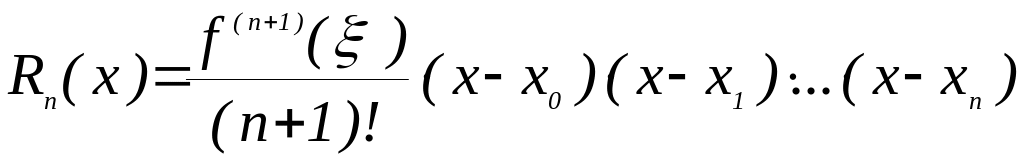где
(
-
некоторая неизвестная точка ).
Отсюда следует оценка погрешности приближения функции (в текущей точке)
интерполяционным полиномом Лагранжа
;
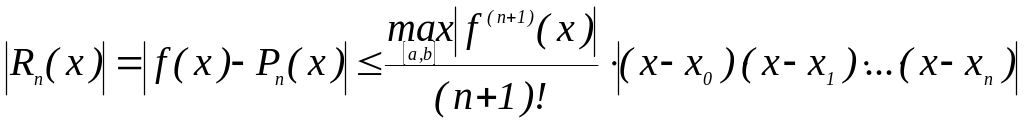1-й интерполяционной формулой Ньютона
т.к.
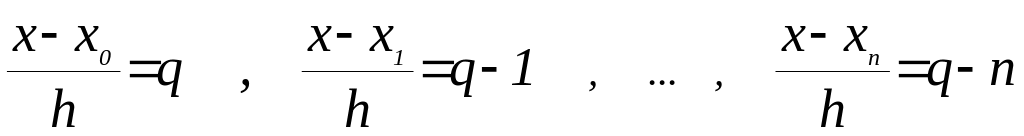, то
,
где q>0;
2-й интерполяционной формулой Ньютона
т.к.
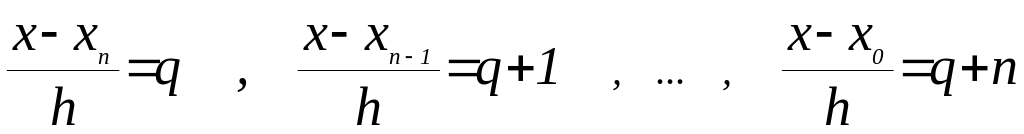, то
,
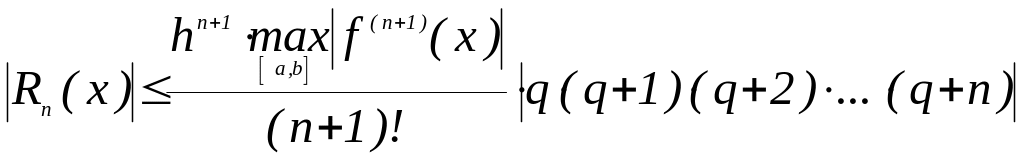где q<0
.
Пример.
Оценить погрешность приближения функции
в точке
интерполяционным полиномом в форме
Лагранжа с узлами x0
=100
,
x1 = 121 ,
x2 = 144 .
;
;
;
;
.
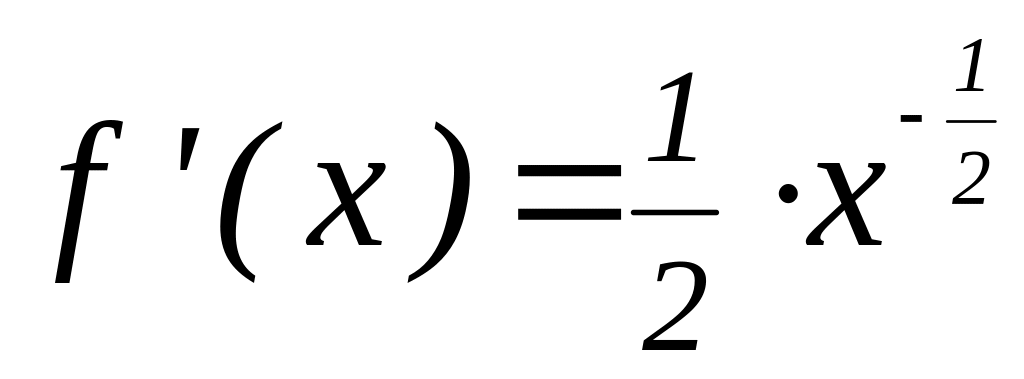
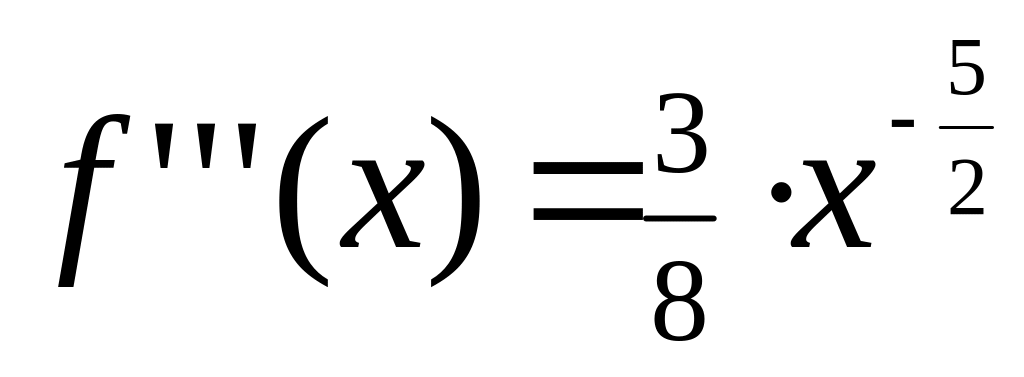