Лабораторная работа № 1

Приближенное решение алгебраических и трансцендентных уравнений

Цель работы: изучение методов численного решения нелинейных уравнений.

Содержание работы

1. Изучение

а) аналитического способа отделения корней;

б) численных методов уточнения корней:

• дихотомии,

• хорд,

• касательных,

• комбинированного,

• итераций.

2. Применение численных методов для решения алгебраических уравнений.

3. Реализация вычислительного процесса.

Основные понятия

Алгебраические уравнения (в канонической форме):

а_n x ⁿ + a_n-1 x ^n-1 + ... + a₁x + a₀ = 0

Трансцендентные уравнения -

в которых переменная х находится

под знаком трансцендентной функции:

показательная а ^х;

логарифмическая log _a x ;

тригонометрические sin x ;

cos x ;

.

.

.

tg x ;

Численное решение уравнения (вычисление корней) состоит из нескольких этапов.

Этап 1. Отделение корней

Условия, предъявляемые функции на интервале изоляции корня (рис. 1.1):

- наличие корней;

3)

- монотонность функции.

Рис. 1.1

Случаи поведения на :

1 2 3 4

>0 <0 <0 >0

<0 <0 >0 >0

Рис. 1.2

Аналитический способ отделения корней.

Необходимо найти:

1. Производные и .

2. Критические точки (точки экстремума и точки перегиба): = 0 и .

3. Знаки : а) в критических точках,

б) в граничных точках (определяются D(f), где D(f) - область определения

функции).

4. Интервал, где функция меняет знак: , где .

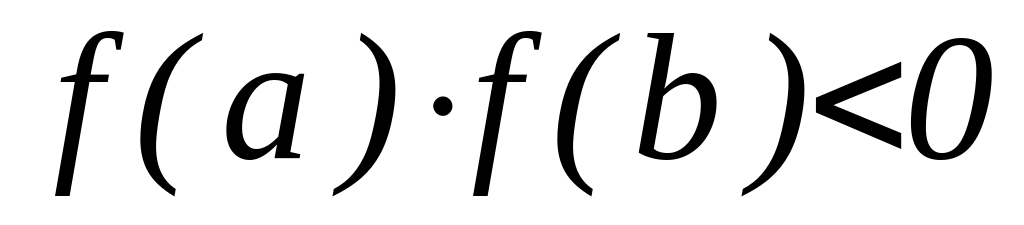Пример. Необходимо отделить корни уравнения x³ – 3x + 1 = 0 .

Определение точек экстремума: = 3x² – 3 = 0 ,

.

Область определения полиномов: D( f ) = ] -  ; +  [.

Построение таблицы знаков функции (табл. 1.1):

Таблица 1.1

x	-	-1	1	+
sign f(x)	-	+	-	+

Вывод: т.к. функция f(х) имеет 3 перемены знака, то уравнение f(х) = 0 имеет 3

действительных корня.

Определение точек перегиба: ,

х = 0 .

Уточненный вариант таблицы знаков функции (с конкретизацией границ) (табл. 1.2 ) :

Таблица 1.2

x	-2	-1	0	1	2
sign f(x)	-	+	+	-	+

Критерий конкретизации границ: замена не влияет на знак функции .

Вывод: ;

[ 0; 1];

[ 1; 2].

Этап 2. Уточнение корней

Процесс уточнения корней осуществляется различными методами .

Метод дихотомии (половинного деления)

Р ассмотрим случай 3 ( см. рис. 1.2, рис. 1.3 ).

Рис. 1.3

1. Вычисляется _.

2. Определяется ,

если

Сужение интервала .

и т. д.

В результате формируется последовательность х₀, x₁, x₂, ..., x_n, ... ,

3. Производится оценка погрешности приближения

,

где - длина интервала изоляции корня на n - й итерации ;

- предельная абсолютная погрешность приближения (заданная точность вычислений).

Если выполняется неравенство – вычисления прекращаются и

  x_{n .}

Пример. Необходимо методом дихотомии уточнить корень уравнения

х ³ - 3 х +1 = 0 с точностью 10 ^–3 (табл. 1.3) .

Таблица 1.3

n	a n	b n		f(x n)
0	0	1	0,5	-0,375
1	0	0,5	0,25	0,2656
2	0,25	0,5	0,375	-0,0723
3	0,25	0,375	0,3125	0,0930
4	0,3125	0,375	0,3438	0,0092
5	0,3438	0,375	0,3594	-0,0318
6	0,3438	0,3594	0,3516	-0,0113
7	0,3438	0,3516	0,3477	-0,0011
8	0,3438	0,3477	0,3458	0,0040
9	0,3458	0,3477	0,3468	0,0013
10	0,3468	0,3477	0,3473

a₁₀ - b₁₀ = 0,3468 – 0,3477 = 0,0009 < , где = 0,001.

  0,347 .

Метод хорд (пропорциональных частей)

Идея метода состоит в замене на хордой .

Р ассмотрим случай 3 ( см. рис. 1.2, рис.1.4).

Рис. 1.4

Выбор начального приближения : в качестве выбирается тот конец , для которого

.

В данном случае x₀ = b.

Уравнение хорды :

Рассмотрим : полагая y=0 и x=x₁ находим

,

где x₁ – 1-е приближение.

Аналогично для : полагая y=0 и x=x₂ находим

,

где x₂ – 2-е приближение.

.

.

.

Рекуррентная формула для вычисления последовательных приближений имеет следующий вид:

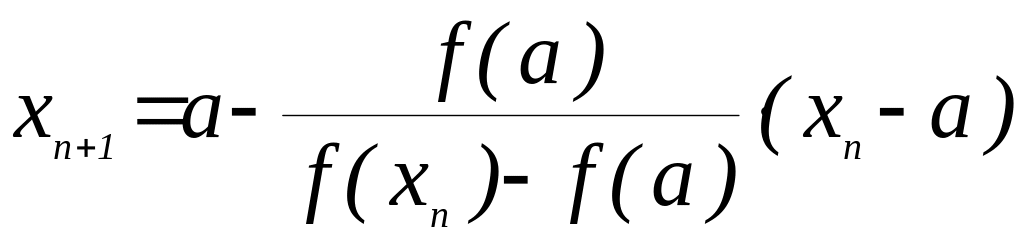, (n = 0,1,2,...). (1.1)

В результате формируется монотонная убывающая последовательность

a<<...<x_n+1<x_n<...<x₁<x₀=b .

Замечание . В случаях 1 и 3 (см. рис. 1.2) начальное приближение х₀ = b и вычисления ведутся по формуле (1.1) .

В случаях 2 и 4 (см. рис. 1.2) начальное приближение х₀ = а , а рекуррентная формула принимает вид :

( n = 0, 1, 2,…).

Оценка погрешности приближения

При n  N , где N - определенное число (т. е. начиная с некоторого приближения)

выполняется  - x_n<x_n - x_n-1.

Если  x_n - x_n-1<  , то - x_n<  .

Пример. Необходимо методом хорд уточнить корень   [0;1] уравнения

х ³ - 3х + 1 = 0 с точностью 10 ^–3 (табл. 1.4) .

;

а = 0 ; f(a) = 1.

Таблица 1.4

n	х n	x n - a	f(x n )
0	1	1	-1	-0,5
1	0,5	0,5	-0,375	-0,3636
2	0,3636	0,3636	-0,0427	-0,3487
3	0,3487	0,3487	-0,0037	-0,3474
4	0,3474	0,3474	-0,0003	-0,3473
5	0,3473

x ₅ - x ₄ < .

  0,347.

Метод касательных ( Ньютона )

Идея метода состоит в замене дуги кривой y=f(x) на ее касательной .

Рассмотрим случай 3 (см. рис. 1.2, рис.1.5).

Рис. 1.5

Выбор начального приближения : в качестве x₀ выбирается тот конец , для которого

.

В данном случае x₀=a.

Уравнение касательной : .

Рассмотрим : полагая y=0 и x=x₁ находим

,

где x₁ – 1-е приближение.

Аналогично для : полагая y=0 и x=x₂ находим

,

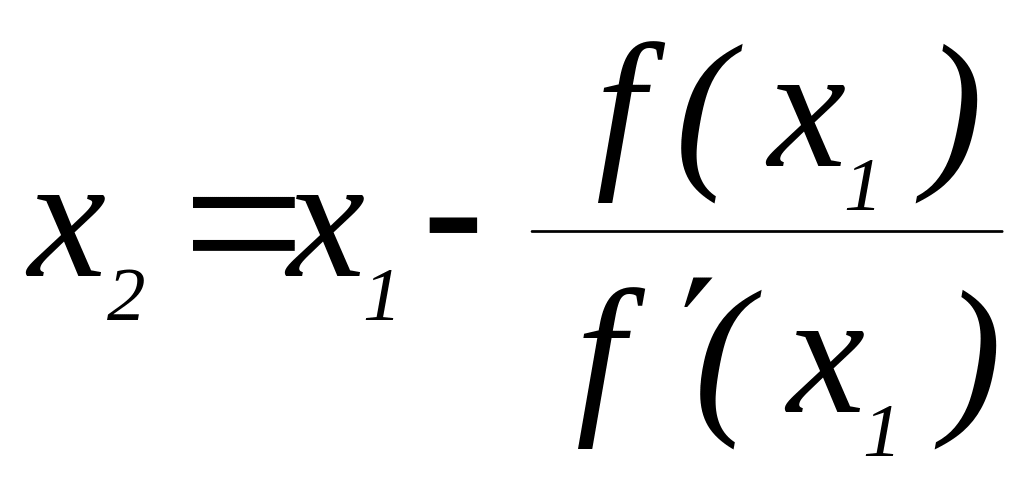где x₂ – 2-е приближение.

.

.

.