
- •1. Wymien podstawowe wielkosci fizyczne ukladu si oraz podaj ich jednostki. Przedstaw
- •3. Omów kartezjański I biegunowy dwuwymiarowy układ odniesienia oraz kartezjański,
- •Związki pomiędzy współrzędnymi cylindrycznymi oraz kartezjańskimi [edytuj]
- •10. Omów poznane zasady zachowania obowiazujace w mechanice.
- •12. Omów ruch harmoniczny ciala na przykladzie oscylatora harmonicznego prostego lub
- •Analiza ruchu wahadła
- •17. Omów zjawisko dudnienia I przyklad wykorzystania tego zjawiska.
- •20. Omów plaska fale harmoniczna I zapisz równanie fali plaskiej.
- •21 Omów zjawisko dyfrakcji I interferencji fal, przedstaw rysunki I zapisz wzory.
- •24 Jakie wielkosci charakteryzuja fale dzwiekowa? Przedstaw wzory na cisnienie, energie,
- •30 Jaki proces nazywamy odwracalnym, a jaki nieodwracalnym? Podaj przyklady procesów odwracalnych I nieodwracalnych.
- •35. Zapisz równanie Van der Waalsa I omów izotermy gazu rzeczywistego. Kiedy mamy do czynienia z równowaga fazowa - podaj przyklady?
- •37. Przedstaw konstrukcje powstawania obrazów w zwierciadlach wkleslych I soczewkach
- •38 Omów budowe siatki dyfrakcyjnej I opisz sposób wyznaczania dlugosci fali swietlnej.
- •39 Omów promieniowanie ciala doskonale czarnego, opisz prawo Kirchhoffa, Stefana-
- •I jak okreslamy energie tego promieniowania?
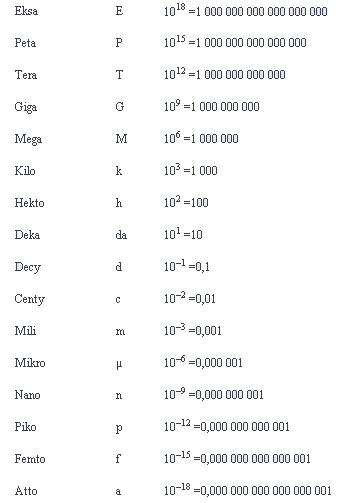
1. Wymien podstawowe wielkosci fizyczne ukladu si oraz podaj ich jednostki. Przedstaw
oznaczenia poznanych wielokrotnosci i podwielokrotnosci jednostek wielkosci
fizycznych.
Podstawowe jednostki układu SI:
nazwa-jednostka-oznaczenie-podwielokrotności.
metr- m – długość - milimetr, centymetr, decymetr, metr, kilometr
kilogram – kg – masa - gram,dekagram, kilogram, tona
sekunda - s – czas - sekunda, minuta, godzina
amper- A – natężenie prądu elektrycznego
kelwin – K – temperatura
kandela- cd – natężenie światła, światłość
mol- mol – liczność materii
Są też dwie jednostki tzw. pomocnicze: radian [rad](miara kąta płaskiego) i steradiad [sr](miara kąta bryłowego).
2. Podaj przykłady wielkości skalarnych i wektorowych. Opisz poznane działania na
wektorach.
Skalarne - długość (mm, cm, m, km), pole (m kwadratowe, km kwadratowe), objętość (dm sześcienne, m sześcienne), temperatura (celsjusze, kelwiny), gęstość (kg/m sześcienny) wektorowe - siła (jule), prędkość (km/h, m/s), przyspieszenie (m/s do kwadratu)
Suma wektorów:

Aby dodać do siebie dwa wektory
u→ i w→ należy obrać sobie dowolny punkt. W punkcie A zaczepiamy początek wektora równego wektorowi u→.
Jego koniec znajduje się w punkcie B. W punkcie B umieszczamy początek wektora równego wektorowi w→. Jego koniec znajduje się w punkcie C.
Wektor AC→ równy jest wektorowi v→ =u→ +w→ . Wektorami składowymi danego wektora nazywa się wektory, których suma jest równa danemu wektorowi.
Wektor będący sumą kilku wektorów nazywany jest wektorem wypadkowym.
różnica wektorów:
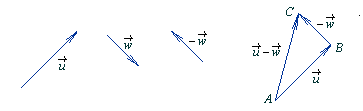
Różnicą wektorów u→ i w→ nazywamy sumę wektorów u→ i przeciwnego do w→.
v→ = u→ - w→= u→ + (-w→)
Mnożenie wektora przez liczbę (skalar)
Iloczyn danego wektora u→
przez skalar s, to wektor v→ =s *u→ o tym samym kierunku, ale długości stanowiącej iloczyn długości wektora przez wartość skalara s i zwrocie zgodnym ze zwrotem wektora jeśli s > 0 i przeciwnym gdy s < 0. Iloczynem dowolnego wektora i liczby s = 0 jest wektor zerowy, a także iloczynem wektora zerowego i dowolnej liczby jest wektor zerowy.Tak określone mnożenie spełnia podstawowe własności algebraiczne - jest łączne i rozdzielne.
3. Omów kartezjański I biegunowy dwuwymiarowy układ odniesienia oraz kartezjański,
cylindryczny i sferyczny trójwymiarowy układ odniesienia.
*dwuwymiarowy kartezjański układ odniesienia
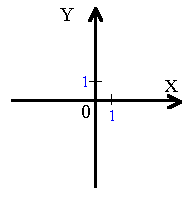
Na płaszczyźnie układ kartezjański stanowią dwie prostopadle ustawione osie X i Y (lub też określanych jako OX i OY). Punkt przecięcia tych osi wyznacza zero układu współrzędnych.
Aby układ był w pełni zdefiniowany należy na obu osiach zaznaczyć wartości jednostkowe.
Oś X nazywana jest osią odciętych, podczas gdy oś Y, to oś
rzędnych.
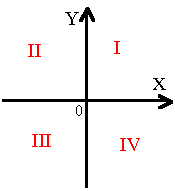
Ćwiartki układu współrzędnych
Układ XY dzieli całą płaszczyznę na cztery ćwiartki numerowane przeciwnie do ruchu wskazówek zegara:
|
I ćwiartka - dodatnie X i dodatnie Y |
|
II ćwiartka - ujemne X i dodatnie Y |
|
III ćwiartka - ujemne X i ujemne Y |
|
IV ćwiartka - dodatnie X i ujemne Y |
*trójwymiarowy kartezjański układ odniesienia
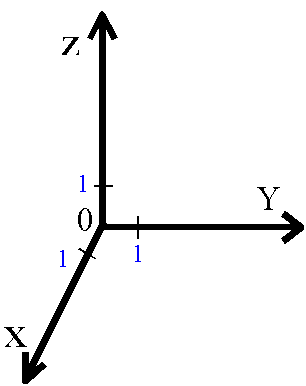
Układ trzech współrzędnych kartezjańskich XYZ rysujemy w sposób prawoskrętny (posługując się regułą śruby prawoskrętnej). Oznacza to, że zwrot osi Y jest zależny od nazwania osi X i Z. Gdybyśmy wkręcali śrubę (prawoskrętną, czyli taką jak wszystkie typowe śruby w Polsce) w kierunku od osi X do osi Y, to śruba ta powinna posuwać się (wkręcać) wskazując zwrot osi Z.
Położenie punktu w przestrzeni w układzie kartezjańskim podaje się za pomocą trzech liczb X,Y,Z - współrzędnych x-owej, y-owej i z-wej. Np. P(1,3,2) oznacza, że współrzędne x-owa punktu ma wartość -1 y-owa ma wartość 3, a z-owa ma wartość 2.
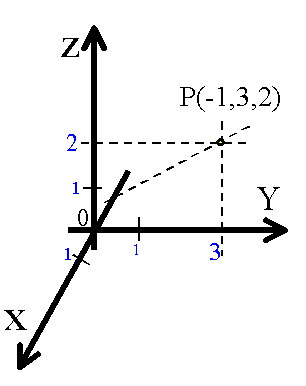
*dwuwymiarowy biegunowy układ współrzędnych
Układ biegunowy (w odniesieniu do rozważań przestrzennych nazywany "walcowym") jest wygodny do stosowania wtedy, gdy analizujemy obroty ciał.
W układzie tym zamiast posługiwać się współrzędnymi X i Y (i w przestrzeni Z), wprowadza się dwie współrzędne innego rodzaju:
|
promień R (promień wodzący) |
|
kąt φ jaki tworzy wektor wodzący z osią X-ów. |
|
dla rozważań przestrzennych oś Z pozostaje bez zmian |
Układ biegunowy jest wygodny, gdy trzeba opisywać ruchy obrotowe. Po umieszczeniu środka układu współrzędnych dokładnie w osi obrotu (prostopadłej do płaszczyzny obrotu) promień wodzący dla danego punktu jest stały. Wtedy dość często ruch może być opisywany tylko za pomocą zmian tylko jednej współrzędnej – kąta φ.
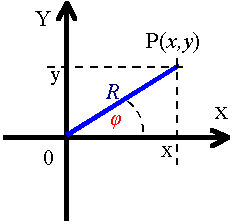
Pomiędzy współrzędnymi w układzie biegunowym i kartezjańskim zachodzą proste związki:
![]() tg
φ = y/x
tg
φ = y/x
Przekształcenie odwrotne wygląda następująco:
x = R cos φ y = R sin φ
*trójwymiarowy cylindryczny układ odniesienia
Walcowy układ
współrzędnych
(cylindryczny układ
współrzędnych)
to układ
współrzędnych
w trójwymiarowej przestrzeni
euklidesowej.
Każdy punkt P
przestrzeni zapisuje się w postaci trójki współrzędnych
![]() ,
gdzie poszczególne składowe wyrażają się następująco:
,
gdzie poszczególne składowe wyrażają się następująco:
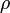 —
odległość od osi OZ
rzutu punktu
—
odległość od osi OZ
rzutu punktu
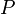 na
płaszczyznę OXY,
na
płaszczyznę OXY,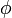 —
kąt pomiędzy osią dodatnią
OX
a odcinkiem łączącym rzut punktu P
na płaszczyznę OXY z początkiem układu współrzędnych,
—
kąt pomiędzy osią dodatnią
OX
a odcinkiem łączącym rzut punktu P
na płaszczyznę OXY z początkiem układu współrzędnych,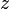 —
odległość rzutu punktu P
na oś OZ od początku układu współrzędnych.
—
odległość rzutu punktu P
na oś OZ od początku układu współrzędnych.
Wektor
wodzący
układu walcowego
![]() łączy
źródło pola z punktem P :
łączy
źródło pola z punktem P :
![]()
