Задача 3

Задача содержит расчет трехфазной цепи переменного тока при соединении приемников электрической энергии в звезду или треугольник. Студенты должны разобраться в заданной схеме соединения и в соотношениях линейных и фазовых токов и напряжений для этой схемы.

1. Определить полное сопротивлений каждой фазы приемника энергии потребителя:

, при этом X = X_L – X_C.

2. Определить фазное напряжение U_ф в зависимости от схемы соединения:

• для треугольника: U_ф = U_Л;

• для звезды: U_ф = U_Л .

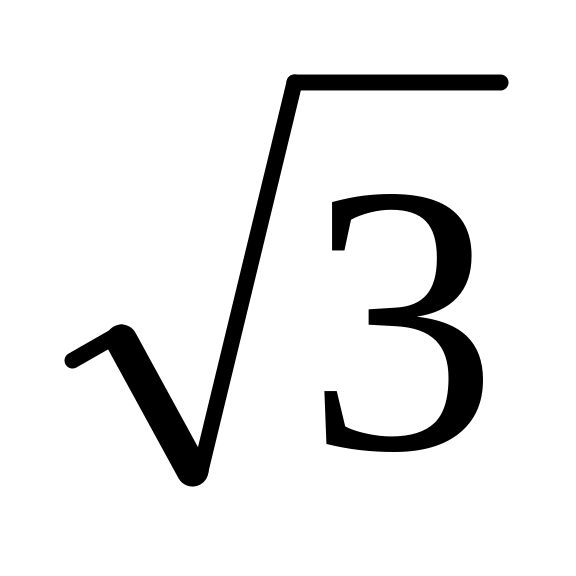3. Определить токи в каждой фазе потребителя .

4. Активная мощность трехфазной цепи равна сумме активных мощностей фаз, которые можно определить, зная ток и сопротивление каждой фазы:

• для треугольника: ;

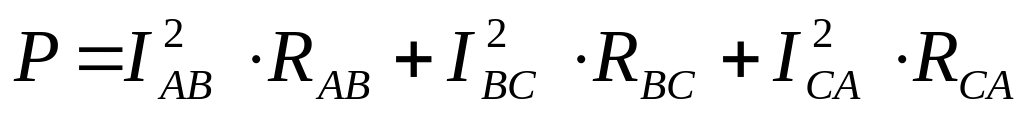• для звезды: .

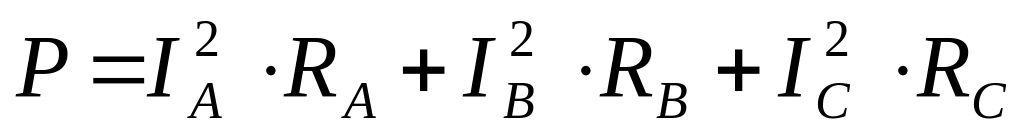5. Определить линейные токи I_A, I_B, I_C в зависимости от схемы соединения:

для звезды I_A=I_ф;

для треугольника проще всего найти токи I_A графически из векторной диаграммы (см. п.6). Аналитическое определение линейных токов производится по теореме косинусов для косоугольного треугольника:

; (α = 120° – φ_СА – φ_АВ);

; (β = 120° – φ_АВ – φ_ВС);

; (γ = 120° – φ_ВС – φ_СА).

Угол φ определяется для каждой фазы или .

6. При соединении треугольником напряжения U_ф = U_л, поэтому построение векторной диаграммы начинаем с построения в выбранном масштабе векторов фазных и линейных напряжений.

Угол сдвига по фазе между U_ф и I_ф зависит от характера нагрузки. При активной U_ф и I_ф совпадают, при активно-индуктивной – I_ф отстает от U_ф на угол φ, при активно-емкостной – I_ф опережает U_ф на угол φ. Определив угол φ в каждой фазе потребителя ( ) строим токи I_ф, затем по уравнению:

I_A = I_AB - I_CA

I_B = I_BC - I_AB

I_C = I_CA - I_BC

строим линейные токи и определяем их числовое значение.

7. При соединении звездой с нулевым проводом фазные напряжения U_ф равны между собой и определяются .

Построение векторной диаграммы начинаем с построения в выбранном масштабе векторов фазных напряжений U_A, U_B, U_C.

Линейные напряжения строим по уравнениям: U_AB = U_A - U_B.

Токи I_ф = I_л строим в зависимости от угла φ в каждой фазе.

Строим ток нулевого провода I_N = I_A·I_B·I_C и определяем его величину.

Рассмотрим пример. Пусть заданы схема цепи (рис.12), ее параметры: U_л=36 В; X_C=X_L=5,2 Ом; R=9 Ом. Напряжение фаз источника и нагрузки одинаковы: В.

А; А.

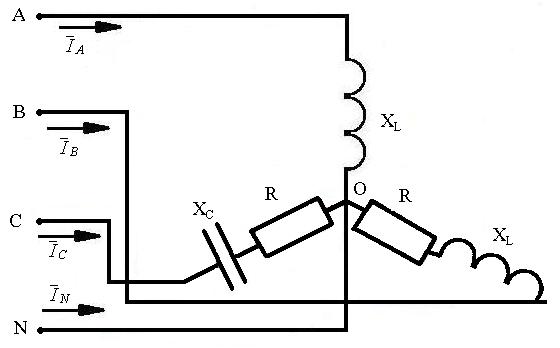
Рисунок 12. Схема соединения потребителей электрической энергии в звезду

Для звезды линейные токи равны токам фаз А.

Построение векторной диаграммы (рис.13) начинаем с построения в выбранном масштабе векторов линейных и фазных напряжений.

Угол сдвига по фазе между током и напряжением можно найти из треугольника сопротивлений. В активно-индуктивной нагрузке ток по фазе отстает от напряжения, а в активно-емкостной нагрузке опережает его на угол φ. Для данной схемы: φ_А=90°, φ_В=30°, φ_С=-30°. На основании первого закона Кирхгофа для узла «О» ток нулевого провода I₁ равен геометрической сумме токов фаз I_А, I_В, I_С: I_N = I_А + I_В + I_С.

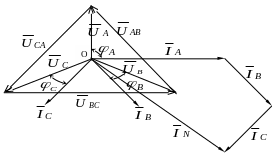
Рисунок 13. Векторная диаграмма