
- •Векторное произведение векторов
- •Свойства векторного произведения
- •Смешанное произведение векторов
- •Плоскость.
- •Линии второго порядка
- •Исследование функций на экстремум. Выпуклость и вогнутость кривой, точки перегиба. Асимптоты
- •Исследование функций и построение их графиков
- •4.8. Поверхности второго порядка
- •Предел числовой последовательности. Предел функции
- •Бесконечно малые и бесконечно большие функции Сравнение бесконечно малых. Непрерывность функции. Точки разрыва и их классификация
- •Производные и дифференциалы высших порядков. Дифференцирование функций, заданных параметрически
- •Формула Тейлора и ее приложения
Матрицы
Прямоугольная таблица из чисел вида
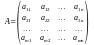 ,
,
состоящая из m строк и n столбцов, называется матрицей размеров m n.
Матрица
 называется обратной к квадратной
матрице А,
если
называется обратной к квадратной
матрице А,
если
 ,
где Е –
единичная матрица. Для невырожденной
матрицы
,
где Е –
единичная матрица. Для невырожденной
матрицы
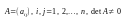 ,
где
,
где
 – определитель матрицы А,
существует единственная обратная
матрица
– определитель матрицы А,
существует единственная обратная
матрица
 ,
,
где
 – алгебраические дополнения элементов
– алгебраические дополнения элементов
 матрицы А.
матрицы А.
Если матрица А
– вырожденная
 ,
то обратной к ней не существует.
,
то обратной к ней не существует.
Системы линейных уравнений. Матричный
метод.Правило Крамера. Метод Гаусса
Пусть задана система n линейных уравнений с n неизвестными вида
 (4.1)
(4.1)
или, в матричной форме
А Х = В,
где

Формулы Крамера. Если система (4.1) невырождена, то она имеет единственное решение, определяемое формулами Крамера:

где
 – определитель, получаемый из определителя
– определитель, получаемый из определителя
 заменой его i-го
столбца на столбец В
свободных членов.
заменой его i-го
столбца на столбец В
свободных членов.
Матричный метод.
Решение невырожденной
системы (4.1) можно найти по формуле
 .
.
Метод последовательного исключения неизвестных (метод Гаусса).
С помощью элементарных преобразований над строками система m линейных уравнений с n неизвестными может быть приведена к виду
 ,
(4.2)
,
(4.2)
где

Система
(4.2) эквивалентна исходной системе. Если
хотя бы одно из чисел
 отлично от нуля, то система (4.2), а
следовательно,
и исходная система несовместны. Если
же
отлично от нуля, то система (4.2), а
следовательно,
и исходная система несовместны. Если
же
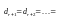
 то
система совместна и из уравнений (4.2)
выражают последовательно неизвестны
то
система совместна и из уравнений (4.2)
выражают последовательно неизвестны через
через
 .
.
Скалярное произведение векторов в R3
Скалярным
произведением векторов
 и
и
 называется число, обозначаемое
называется число, обозначаемое
 или
или
 и равное
и равное
 где
где
 – угол между
и
.
– угол между
и
.
Свойства скалярного произведения:
1.
 2.
2.

3.
 4.
4.

Свойство 4 выражает условие ортогональности векторов.
Если векторы
 и
и
 представлены своими
координатами в ортонормированном
базисе
представлены своими
координатами в ортонормированном
базисе
 ,
то скалярное
про-изведение равно
,
то скалярное
про-изведение равно
 Из
этой формулы и определения скалярного
произведения следует:
Из
этой формулы и определения скалярного
произведения следует:

Учитывая, что
 где
где
 – проекция вектора
на вектор
,
а
– проекция вектора
на вектор
,
а
 скалярное произведение векторов
скалярное произведение векторов
 можно записать в виде
можно записать в виде

Механический
смысл скалярного произведения:
работа А,
про-изводимая силой
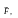 точка приложения которой перемещается
из точки
точка приложения которой перемещается
из точки
 в точку
в точку
 вычисляется по формуле
вычисляется по формуле

Векторное произведение векторов
Упорядоченная
тройка некомпланарных векторов
 называется правой, если при наблюдении
из конца третьего вектора кратчайший
поворот от первого ко второму виден
против часовой стрелки; в противном
случае тройка называется левой (рис.
4.1).
называется правой, если при наблюдении
из конца третьего вектора кратчайший
поворот от первого ко второму виден
против часовой стрелки; в противном
случае тройка называется левой (рис.
4.1).

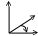
Рис. 4.1: а
– тройка
 правая; б
– тройка
левая
правая; б
– тройка
левая
Векторным
произведением вектора
на вектор
называется вектор
 удовлетворяющий условиям:
удовлетворяющий условиям:
1)
 – угол между векторами
и
;
– угол между векторами
и
;
2)

3) Упорядоченная
тройка
 – правая.
– правая.
Обозначение:

Свойства векторного произведения
1)

2)

3)

4)
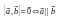 – условие коллинеарности векторов.
– условие коллинеарности векторов.
Если
векторы
 заданы своими коорди-натами
в ортонормированном базисе
,
то
заданы своими коорди-натами
в ортонормированном базисе
,
то

Площадь
параллелограмма, построенного на
векторах
 мож-но определить по формуле
мож-но определить по формуле

Механический
смысл векторного произведения.
Пусть точка А
твердого тела закреплена, а в его точке
В
приложена сила
 .
Тогда возникает вращательный момент
.
Тогда возникает вращательный момент
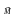 (момент силы). По определению момент
силы относительно точки А
находится по формуле
(момент силы). По определению момент
силы относительно точки А
находится по формуле
 .
.
Смешанное произведение векторов
Смешанным
произведением трех векторов
называется число, получаемое следующим
образом: векторное произведение
 умножается скалярно на вектор
умножается скалярно на вектор
 Смешанное произведение векторов
обозначается
Смешанное произведение векторов
обозначается
 Таким образом,
Таким образом,
 Если векторы
заданы своими координатами в
ортонормированном базисе, то
Если векторы
заданы своими координатами в
ортонормированном базисе, то

Объем параллелепипеда
V,
построенного на векторах
 можно вычислить по формуле
можно вычислить по формуле
 Для того чтобы три вектора
были компланарны, необходимо и достаточно,
чтобы
Для того чтобы три вектора
были компланарны, необходимо и достаточно,
чтобы

Прямая на плоскости.
В декартовой прямоугольной системе координат Оxy прямая на плоскости может быть задана уравнениями:
– общее уравнение прямой
Ax + By + C = 0; (4.3)
– уравнение прямой,
проходящей через точку M0(x0,
y0)
перпендикулярно
нормальному вектору
 :
:
A(x – x0) + B(y – y0) = 0;
– уравнение
прямой, проходящей через точку M0(x0,
y0)
параллельно
направляющему вектору
 (каноническое уравнение прямой):
(каноническое уравнение прямой):

– параметрические уравнения прямой
 ;
;
– уравнение прямой в отрезках

Здесь a и b – величины отрезков, отсекаемых на осях координат Ox и Oy (т.е. длины, взятые с соответствующими знаками);
– уравнение прямой, проходящей через две данные точки M1(x1, y1) и M2(x2, y2):
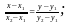
– уравнение прямой с угловым коэффициентом k, проходящей через точку M0(x0, y0):
y – y0 = k(x – x0).
Расстояние
 от точки M0(x0,
y0)
до прямой l,
заданной уравнением (4.3), определяется
по формуле
от точки M0(x0,
y0)
до прямой l,
заданной уравнением (4.3), определяется
по формуле
 .
(4.4)
.
(4.4)
Две прямые, заданные уравнениями A1x + B1y + C1 = 0 и
A2x
+ B2y
+ C2
= 0,
параллельны,
если
 ,
и перпендикулярны, если A1A2
+ B1B2
= 0.
,
и перпендикулярны, если A1A2
+ B1B2
= 0.
