2. Дифракция света

2.1. Основные понятия и формулы

К дифракции относят совокупность явлений, связанных с отклонениями от законов геометрической оптики в среде с заметными неоднородностями (размер неоднородностей сравним с длиной волны света). В соответствии с принципом Гюйгенса – Френеля каждая точка фронта волны является источником вторичных когерентных волн. Пространственное перераспределение интенсивности в результате суперпозиции вторичных когерентных волн и наблюдается при дифракции света.

Если источник света и место наблюдения дифракции находятся вблизи препятствия, наблюдают дифракцию Френеля. В этом случае для решения дифракционной задачи (максимум или минимум света в точке наблюдения? ) световой фронт удобно разбивать на зоны Френеля ([1, §177, с. 286–288] ): фазы колебаний, возбуждаемых соседними зонами Френеля, различаются на .

Разность хода вторичных световых волн до точки наблюдения от соответствующих точек соседних зон Френеля равна . Поэтому амплитуда результирующих колебаний, вызванных совместным действием двух соседних зон, будет равна разности амплитуд колебаний, возбужденных в точке наблюдения волнами, исходящими от каждой зоны в отдельности. Амплитуду результирующих колебаний, возбужденных волнами, исходящими от всего фронта волны, можно представить в виде знакопеременного ряда:

,

где - амплитуда колебаний в точке наблюдения, возбуждаемых действием первой (центральной) зоны Френеля.

- амплитуда волны, идущей от – зоны Френеля.

Действия всего открытого фронта волны в точке наблюдения эквивалентно действию половины первой зоны Френеля , а интенсивность света в этом случае .

Условия дифракционных Если световой фронт содержит четное число зон

минимумов в методе зон Френеля, световые волны ослабляют друг друга,

Френеля в точке наблюдения интенсивность равна нулю.

Условия дифракционных Если световой фронт содержит нечетное число зон

максимумов в методе зон Френеля, в точке наблюдения световые волны

Френеля усиливают друг друга, интенсивность макси-

мальна.

Р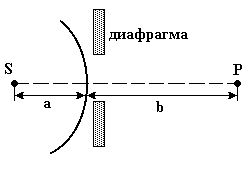 адиус зон Френеля для сферических волн рассчитывается по формуле

, (1) (1)

где a и b – расстояния от источника света S и от точки наблюдения Р до фронта волны; m – номер зоны Френеля (m = 1, 2, ...).

Для плоской волны радиус m зоны Френеля

(2)

Если источник света и точка наблюдения находятся достаточно далеко от препятствия (дифракция происходит в параллельных лучах), то наблюдают дифракцию Фраунгофера.

При дифракции Фраунгофера на одной щели ([1, §179] ) минимум интенсивности наблюдается при условии

(3)

где – ширина щели, - угол дифракции, т.е. угол между нормалью к диафрагме, содержащей щель, и напряжением распространения вторичных когерентных лучей, m – целое число (m – 1, 2, 3…..)

Условие дифракционных максимумов на одной щели

, (4)

где m – порядок дифракционного максимума (m = 0, 1, 2…..)

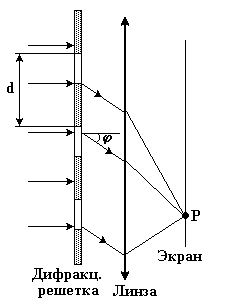
При дифракции Фраунгофера на дифракционной решетке ([1, §180]) максимум интенсивности наблюдается при условии:

У словие главных максимумов при дифракции на дифракционной решетке

Здесь d – период решетки,  – угол между направлениями на центральный максимум (m = 0) и на максимум порядка m.

Угловая дисперсия дифракционной решетки

,

где  – угловое расстояние между спектральными линиями, отличающимися на величину ₀ по длине волны. Линейная дисперсия дифракционной решетки

,

где l – линейное расстояние на экране между спектральными линиями, отличающимися на величину ₀ по длине волны.

Разрешающая способность дифракционной решетки

,

где N – общее число штрихов дифракционной решетки, ₀ – минимальная разность длин волн двух спектральных линий, при которой эти линии воспринимаются раздельно (см [1], §183, с. 295–296).

Условия дифракционных максимумов для дифракции рентгеновских лучей в кристалле

, (9)

где d - межплоскостное расстояние в кристалле,

- длина волны рентгеновского излучения,

m - порядок дифракционного максимума ( )

- угол скольжения (угол между напряжением падающего луча и поверхностного кристалла).