2.2. Рекомендации по решению задач (алгоритм решения)
1. Изобразить схематично ход лучей при дифракции для точки наблюдения Р. Указать на схеме характерные параметры опыта (расстояния, углы и др.).
2. Записать условие максимума или минимума при дифракции (в зависимости от условий задачи).
3. Получить расчетную формулу.
4. Провести вычисления. Проанализировать полученный результат.
2.3. Примеры решения задач
Задача 1
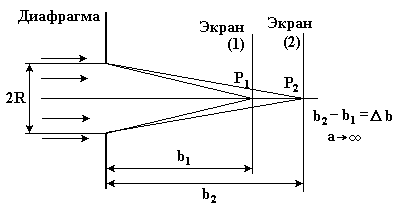
Параллельный пучок монохроматического света с длиной волны 0 = 600 нм нормально падает на диафрагму с круглым отверстием радиусом R = 0,6 мм. В центре экрана, расположенного на расстоянии b1 = 18 см от диафрагмы, наблюдается темное пятно.
На
какое минимальное расстояние b,
измеряемое вдоль оси, перпендикулярной
отверстию, нужно удалить экран, чтобы
в центре его вновь наблюдалось темное
пятно?
Дано:
0 = 600 нм
R = 0,6 мм
b1 = 18 см
__________
b = ?
1. На схеме изображены только крайние лучи из тех, которые формируют картину в точках наблюдения
2. По условию задачи имеем параллельный пучок света. Это означает, что a и формула (8) принимает вид
.
Учтем, что первоначально в центре экрана (в точке Р1) наблюдалось темное пятно (минимум при дифракции Френеля). Следовательно, в отверстии диафрагмы должно укладываться четное число зон Френеля:
R2 = r12 = b1m10, где m1 – четное число.
Чтобы после смещения экрана в положение 2 в центре его (в точке Р2) вновь наблюдалось бы темное пятно, число зон Френеля, укладывающихся в отверстии, должно измениться на 2, т.е. m2 = m1 – 2.
R2 = r22 = b2m20 .
3.
При заданных R, b1,
0
можно найти
.
Тогда
и
.
Окончательно получим для
.
4. Найдем численное значение
.
Заметим,
что задачи на применение метода зон
Френеля традиционно нелегко усваиваются
студентами. Поэтому советуем решить
дополнительно задачи № 16.29, 16.32 [2] , по
ответам в конце сборника задач [2] даны
пояснения.
Задача 2.
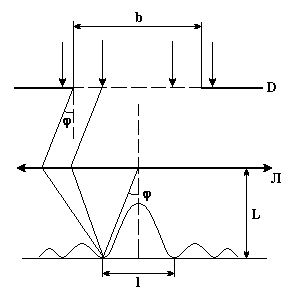
На щель в диафрагме падает нормально монохроматический свет с длиной волны 0 = 600 нм. Дифракционная картина проецируется на экран с помощью линзы, расстояние от линзы до экрана L = 1 м. Ширина центрального максимума на экране l = 3 см. Какова ширина щели?
1. Изобразим схему хода лучей при дифракции света на щели в параллельных лучах.
Здесь же изобразим график распределения интенсивности света при дифракции на щели. В центре картины наблюдается максимум света. Шириной центрального максимума считают расстояние l между ближайшими к нему дифракционными минимумами.
Дано:
0
= 600 нм
L = 1 м
l = 3 см
____________
b = ?
2. Запишем условие минимума при дифракции Фраунгофера на щели (формула (3)):
b sin = m0 , m = 1 по условию задачи.
3.
Из схемы:
Для малых углов sin
= tq
.
Тогда
;
.
Расчетная
формула
.
4.
.
Заметим: при заданных размерах щели b и расстоянии от линзы до экрана L ширина центрального максимума l тем меньше, чем меньше длина волны 0 монохроматического света.
Задача 3
При нормальном падении на дифракционную решетку света от паров натрия желтая линия с длиной волны 1 = 589 нм наблюдается в спектре первого порядка (m = 1) под углом =70 30’.
Оцените: а) период дифракционной решетки d;
б) наибольший (предельный) порядок спектра mпр для линии 1 = 589 нм;
в) минимальную ширину решетки amin, если известно, что в спектре первого порядка разрешены линии желтого дублета натрия (1 = 589 нм и 2 = 589,6 нм);
г) угловое расстояние между линиями желтого дублета в спектре первого порядка.
1. Изобразим ход лучей при дифракции света на дифракционной решетке
Д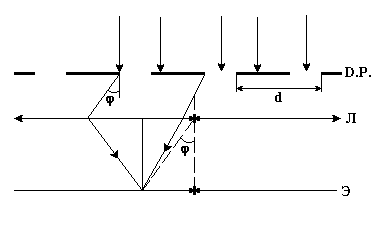
ано
1
= 589 нм
2 = 589,6 нм
m = 1
d = ?
= 70 30’
_______________
mпр = ?
amin = ? = ?
Освещение немонохроматично, соответственно для любого m 0 свет разлагается в спектр.
2. Запишем условия для дифракционных максимумов, формула (5):
d sin = m0.
Нам придется также воспользоваться формулами (6) и (7) для дисперсии и разрешающей способности решетки:
;
.
3. а) задано, что первая желтая линия дублета натрия наблюдается при m = 1 под углом . Это условие позволяет вычислить период решетки:
d sin = m1 ,
;
б) при оценке наибольшего (предельного) порядка спектра учтем, что угол дифракции 900 , sin 1. Подставив sin = 1 в формулу (5), получим расчетную формулу для mпр:
;
в)
по условиям задачи в спектре первого
порядка разрешены линии желтого дублета
1 = 589 нм, 2
= 589,6 нм. Используем формулу для разрешающей
способности решетки R.
Разность длин волн спектральных линий
0 = 2
– 1,
0
=
.
При известном m формула
позволяет оценить
N
– общее число штрихов дифракционной
решетки:
;
.
Зная N и d, найдем ширину решетки a = Nd.
Расчетная формула имеет вид:
;
г) для вычисления углового расстояния между желтыми линиями дублета воспользуемся формулой для угловой дисперсии:
,
отсюда
,
при этом значение cos
оценим для одной из линий дублета.
4. Вычислим искомые величины:
а)
sin
= 0,130;
;
б)
.
Наибольший (предельный) порядок спектра для желтой линии mпр = 7;
в) 0 = 589,6 – 589 = 0,6 нм;
;
;
г)
cos
=0,9915;
.
Задача 4. Определить угол отклонения лучей зеленого света ( = 0,55 мкм) в спектре первого порядка, полученном с помощью дифракционной решетки, период которой d = 0,020 мм.
Дано:
= 0,55 мкм = 5,5 10–7 м
m
= 1
d = 0,020 мм = 2,010–5 м
____________________
Найти .
Из рисунка видно, что оптическая разность хода 21 световых волн, идущих под углом дифракции , после прохождения дифракционной решетки равна
21 = d sin . (1)
Запишем условие максимального усиления световых волн, идущих под углом дифракции (под этим углом наблюдается максимум для зеленого света)
21 = m . (2)
Тогда, учитывая выражения (1) и (2), получаем
d sin φ = m .
Откуда
и
.