2. Дифракция света

2.1. Принцип Гюйгенса–Френеля. Метод зон Френеля. Прямолинейное распространение света. Зонная пластинка

Рис. 16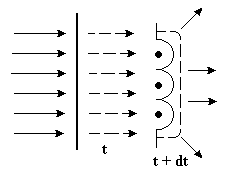

Дифракция света – это огибание световыми волнами препятствий и проникновение в область геометрической тени. Дифракция всегда сопровождается интерференционным перераспределением энергии волны и присуща только волновому движению. Область локализации и масштабы дифракции существенно зависят от соотношения длины волны и размеров препятствий. Наиболее четко дифракция наблюдается тогда, когда длина волны соизмерима с размерами препятствий.

Явление дифракции объясняется с помощью принципа Гюйгенса, согласно которому каждая точка волнового фронта является центром вторичных волн, а огибающая этих волн дает положение волнового фронта в следующий момент време- ни (см. рис. 6.16).

Принцип Гюйгенса, решая задачу о направлении распространения волнового фронта, ничего не говорит об амплитуде, а следовательно, и об интенсивности волн, распространяющихся по разным направлениям. Эту задачу решил Френель, дополнив принцип Гюйгенса идеей интерференции вторичных волн, которые являются когерентными. Учет амплитуд и фаз вторичных световых волн позволяет найти амплитуду результирующей волны в любой точке пространства.

Рис. 17

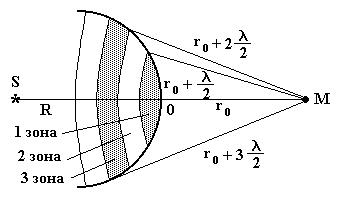
Применим принцип Гюйгенса–Френеля для нахождения амплитуды светового колебания, возбуждаемого в точке М сферической волной, распространяющейся в однородной среде из точечного источника S (см. рис.17).

Пусть R = 0S, а r₀ = 0M. Френель разбил фронт волны на кольцевые зоны (зоны Френеля), построенные так, что расстояния от краев каждой зоны до точки М отличаются на ( – длина световой волны в той среде, в которой распространяется волна). Расстояние r_m от внешнего края m зоны до точки М можно представить в виде

, где m – номер зоны.

И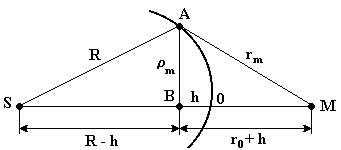 з геометрических рассуждений и рассмотрения SAB и ABM (см. рис. 18) можно получить следующее выражение для радиуса m зоны Френеля

Рис. 18

.

Если волна плоская , то

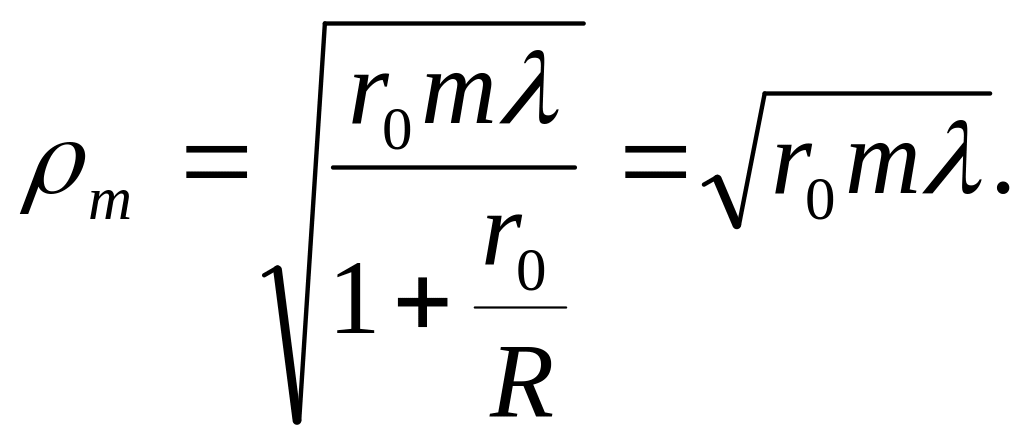
Расчеты показывают, что площади зон Френеля примерно одинаковы. Но так как увеличивается с ростом m по линейному закону, то амплитуда А_m колебания, возбуждаемого в точке М, монотонно убывает с ростом номера зоны, т.е. амплитуды колебаний, возбуждаемых в точке М зонами Френеля, образуют монотонно убывающую последовательность

Фазы колебаний, возбуждаемых соседними зонами, отличаются на  (так как ). Поэтому амплитуда результирующего светового колебания в точке М может быть найдена алгебраически:

или

Можно приближенно считать, что . Тогда все выражения, стоящие в скобках, равны нулю. Пренебрегая последней половинкой амплитуды, находим

.

Таким образом, амплитуда световой волны в точке М равна половине амплитуды, создаваемой лишь одной первой (центральной) зоной Френеля. Действие всей волновой поверхности эквивалентно действию половины центральной зоны. Так как центральная зона имеет размеры долей миллиметра ( << r₀), то свет от источника S к точке М распространяется как бы в узком прямом канале, т.е. прямолинейно.

Если на пути волны поставить непрозрачный экран с отверстием, оставляющим открытым только одну центральную зону Френеля, то амплитуда колебаний в точке М будет равна A₁, т.е. в два раза больше, а интенсивность света – в четыре раза больше, чем при отсутствии экрана.

Еще большего усиления света можно достичь с помощью так называемой зонной пластинки – экрана, перекрывающего либо все четные, либо все нечетные зоны Френеля.