1.4. Расчет интерференционной картины от двух когерентных источников света (опыт Юнга)

С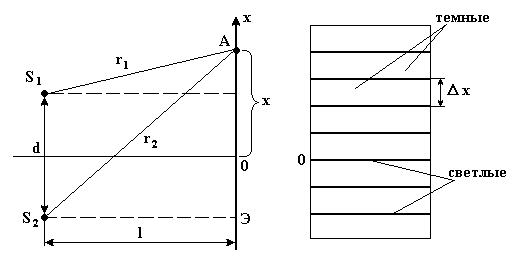 хема опыта Юнга и интерференционная картина в виде светлых и темных полос на экране представлены на рис.7.

Рис. 7

Пусть S₁ и S₂ – когерентные (щелевые) источники света, расположенные на расстоянии d друг от друга, экран Э расположен параллельно d на расстоянии l (l >> d). Световые волны от S₁ и S₂, накладываясь в точке А экрана друг на друга, интерферируют, окрашивая экран прямолинейными полосами (светлыми и темными). Так как световые векторы определяются уравнениями

то разность фаз между волнами

Поскольку источники волн когерентны, то разность начальных фаз и разность фаз

Из рисунка по теореме Пифагора

и .

Вычтем из первого второе равенство

или

.

Опыт показывает, что четкая интерференционная картина наблюдается только вблизи центра экрана, т.е. при x<<l.

Тогда и .

При интерференции механических волн геометрическая разность хода соответствует

(условие максимума),

(условие минимума).

Подставив эти выражения в (1.3), получим

(светлые линии),

(темные линии),

где m = 0, 1, 2 ...

Шириной интерференционной полосы x называется расстояние между соседними минимумами (или максимумами) интенсивности

.

Для немонохроматического света (  const) полосы на экране цветные.

1.5. Оптическая длина пути и оптическая разность хода волн. Интерференция световых волн

Скорость света зависит от свойств среды. Если скорость света в вакууме равна c = 310⁸ м/с, то скорость  света в среде равна , где n – абсолютный показатель преломления среды (n > 1). При переходе световой волны из одной среды в другую изменяется длина волны. Действительно, так как частота световой волны не изменяется, , а скорости света  в разных средах различны, то и длины волн  разные. Для света данной частоты в вакууме длина волны ₀ максимальна:

, т.е.

Произведение геометрической длины пути l, пройденного световой волной в данной однородной среде, на абсолютный показатель преломления этой среды называется оптической длиной пути:

l_опт = ln.

Разность оптических путей двух когерентных волн называется оптической разностью хода этих волн:

г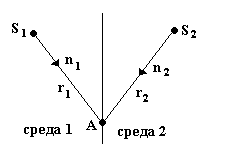 де индекс 21 означает, что из оптического пути волны 2 вычитается оптический путь волны 1. Оптическая разность хода – величина алгебраическая: она может быть положительной или отрицательной.

Рассмотрим интерференцию двух световых волн

и , распространяющихся в разных средах (cм. рис. 8).

К

Рис. 8

вадрат результирующей амплитуды при сложении колебаний, направленных вдоль одной прямой, определяется выражением

где

Так как волны когерентны, то разность начальных фаз

Так как и , то

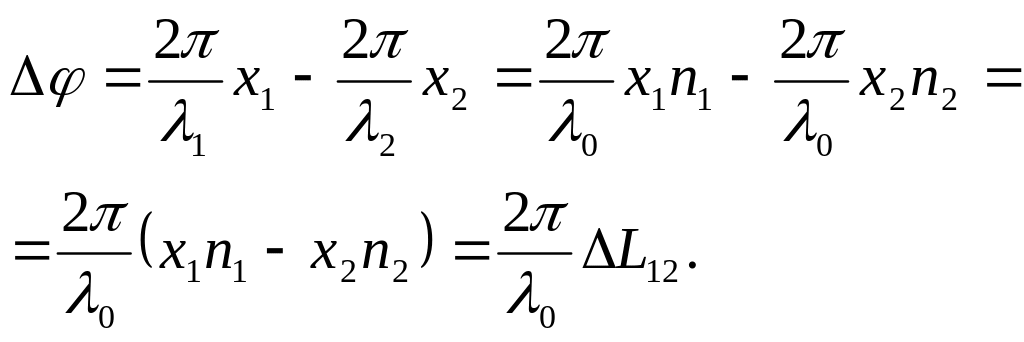
Поскольку волны когерентны, то (не изменяется с течением времени).

Из выражения (1.7) следует, что максимальное усиление волн будет наблюдаться тогда, когда , т.е. , где – целое число.

; .

Оптическая разность хода волны равна четному числу полуволн (условие максимума интенсивности).

Наибольшее ослабление интерферирующих световых волн наблюдается при , .

, .

Оптическая разность хода волн равна нечетному числу полуволн (условие минимума интенсивности).

Интенсивность волны – это энергия, переносимая волной за единицу времени через единичную площадку, перпендикулярную к направлению распространения волны.

Из теории колебательных процессов известно, что энергия волны прямо пропорциональна квадрату амплитуды. Тогда выражение (1.7) может быть записано в виде

При этом , так как когерентные волны не могут быть перпендикулярными.

Напротив, для некогерентных волн (для реальных оптических процессов) среднее по времени значение и , т.е. интенсивность результирующей волны в каждой точке волнового поля равна сумме интенсивностей накладывающихся волн.