Задание 5

Комплексные числа и действия над ними

1. Цель работы

Научиться оперировать с комплексными числами и отображать их на плоскости.

2. Основные теоретические положения

См. раздел 2.1 (с.36, 37) УМК и раздел 3 Учебного пособия (с.19-23).

3. Порядок выполнения работы

Пример 1.

Найти сумму и разность чисел и .

□Числа даны в показательной форме, однако, операции алгебраического суммирования удобнее производить над числами, записанными в алгебраической форме, т.к. достаточно соответствующие действия выполнить отдельно для вещественных и отдельно для мнимых частей чисел, т.е.

(5)

i,

, .

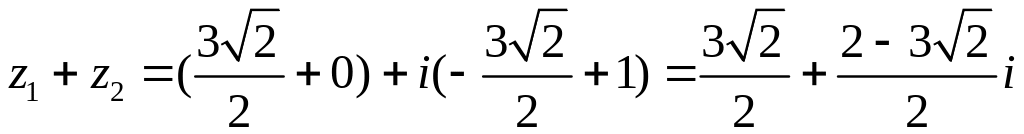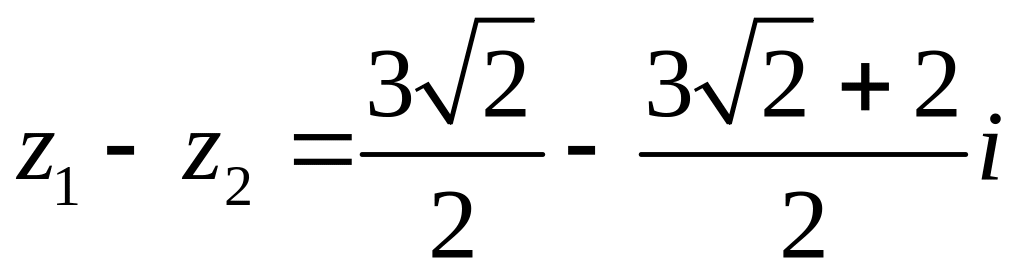Учитывая, что , построим все числа на рис. 1.■

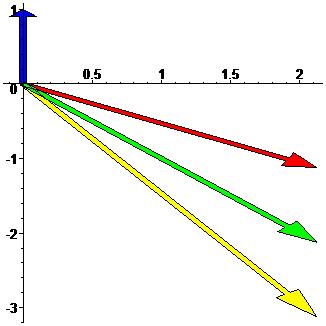
Рис. 1

Пример 2.

Найти произведение и частное чисел .

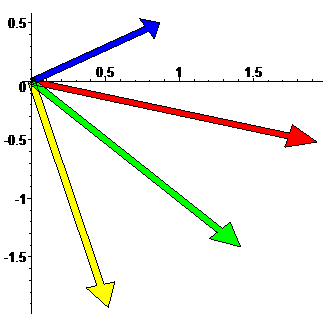
□Находя z₁z₂ поступим с числами, как с обычными алгебраическими многочленами, учитывая, что

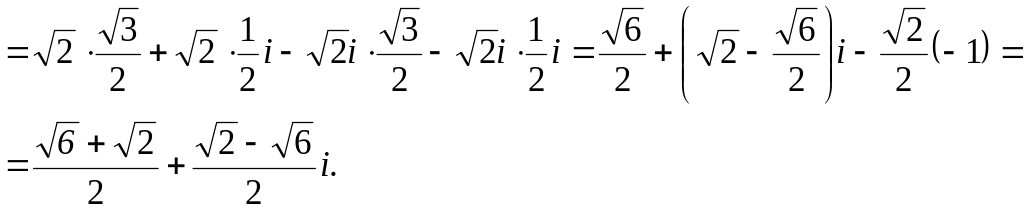
Чтобы найти частное, следует освободиться в знаменателе от комплексного числа, для этого и числитель и знаменатель нужно умножить на число, сопряженное знаменателю.

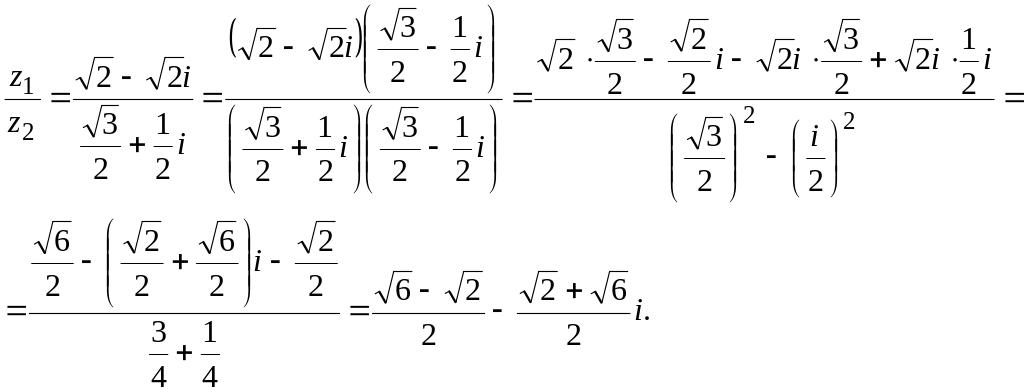
На рис.2 представлены все числа.■

Рис.2

Задание 6

Вычисление производных функции комплексного переменного

1. Цель работы

Научиться вычислять производные от ФКП.

2. Основные теоретические положения

См. раздел 2.2 УМК (с.37-39) и раздел 4.2 Учебного пособия (с.26-29).

Пример.

Вычислить производную функции в точке z₀=πi.

□Для того чтобы функция была аналитической в некоторой области необходимо и достаточно, чтобы её вещественная и мнимая части были определены и непрерывны в этой области и удовлетворяли условиям Коши- Римана, т.е.

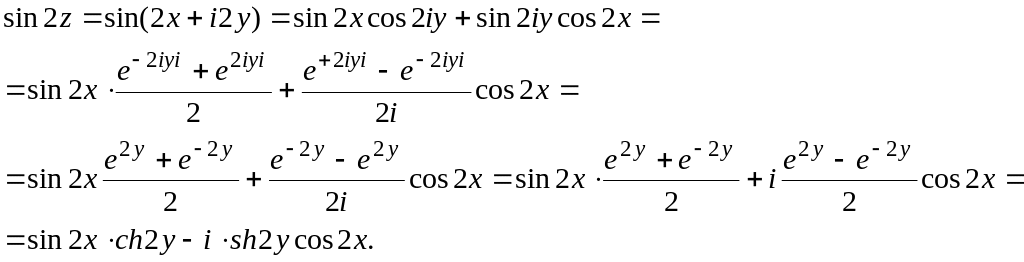
(воспользовались формулами ;

).

Таким образом, u(x,y)=sin2x ch2y; v(x,y)=-sh2y cos2x. Обе функции определены и непрерывны на всей комплексной плоскости. Осталось показать, что они удовлетворяют условиям Коши- Римана. Для этого нужно найти частные производные u(x,y) и v(x,y).

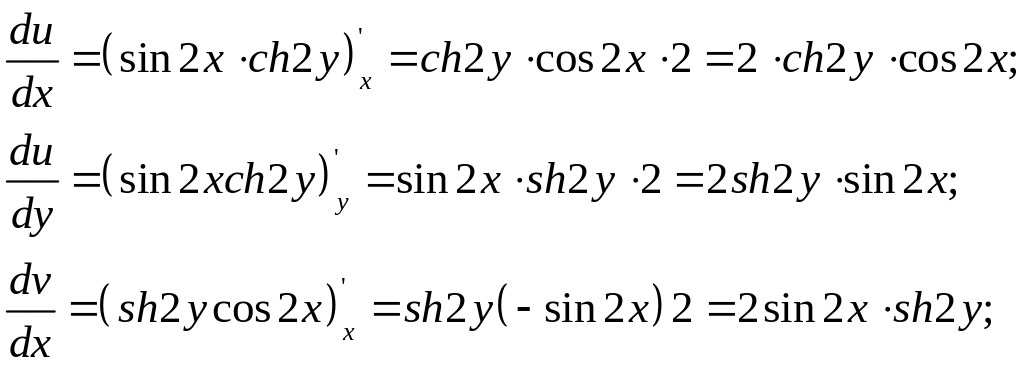
Таким образом , т.е. условия Коши- Римана выполнены. Следовательно, рассматриваемая функция аналитическая по всей числовой плоскости. Производную можно найти, воспользовавшись одной из формул:

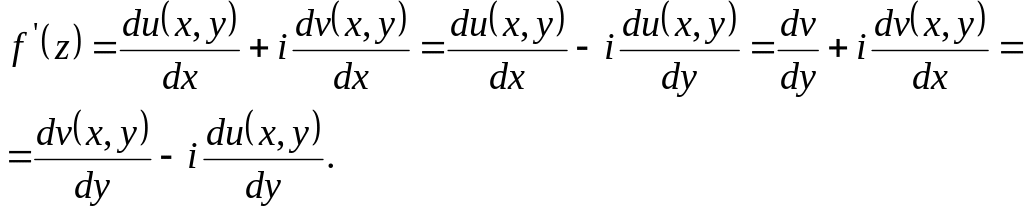
Однако, имея в виду, что для аналитических функций справедливы все правила и формулы дифференцирования функции действительного аргумента, можно избежать применения этих формул.

_■

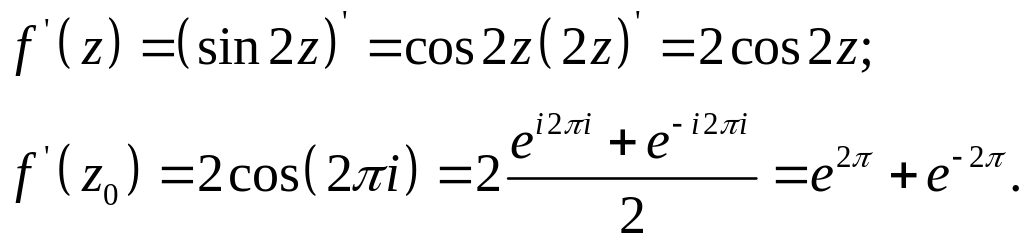Задание 7

Интегрирование функции комплексного переменного

1. Цель работы

Научиться определять тип особых точек и вычислять интегралы от функций комплексного переменного с помощью вычетов.

2. Основные теоретические положения

См. раздел 2.4 УМК (с.41-44) и раздел 6 (с.36-49) Учебного пособия.

Пример 1.

Вычислить интеграл .

(Обход контура в положительном направлении).

□Контур интегрирования – окружность радиусом 2 и центром в точке (-3;0) (рис. 1).

Здесь подынтегральная функция аналитическая везде, кроме точек х₁=0; х₂=2i; x₃=-2i. Эти точки лежат вне области, ограниченной контуром интегрирования, следовательно, можно применить интегральную теорему Коши, согласно которой, интеграл по контору,

Рис. 1.

ограничивающему область аналитичности функции, равен нулю. Таким образом, .

В тех случаях, когда в области, ограниченной контуром интегрирования, подынтегральная функция имеет особые точки, для вычисления интеграла применяется теорема Коши о вычетах: , при условии, что f(z) непрерывна на границе интегрирования и аналитическая всюду внутри области, кроме конечного числа особых точек z₁, z₂,…, z_n.

Таким образом, для того чтобы вычислить интеграл по замкнутому контуру, необходимо определить особые точки, принадлежащие области, ограниченной контуром интегрирования, и вычислить вычеты в этих точках (resf(z_k)).

Напомним, что изолированные особые точки могут быть устранимыми, полюсами (простыми и порядка m), а также существенно особыми точками.

Особая точка называется устранимой особой точкой, если существует конечный предел , вычет в этой точке resf(z₀)=0.

Особая точка называется полюсом, если . Порядок полюса определяется кратностью нуля z₀ функции .

Вычет в простом полюсе вычисляется по формуле

(1)