Вопросы для самопроверки по теме 1.4

1. Что называется суммарной невязкой?

2. В чём состоит условие минимума функции нескольких переменных?

1.5. Многомерные задачи

Одной из многомерных задач является приближение функции нескольких переменных. В этом случае часто используют метод наименьших квадратов, который для одномерного случая рассматривался нами в предыдущей теме. Построив аппроксимирующую функцию, мы естественным образом можем её дифференцировать и интегрировать.

Другим способом получения приближения функции является т.н. метод Монте-Карло. Применение его предполагает знакомство с теорией вероятности, которая является второй частью курса вычислительной математики. Поэтому вопросы темы 1.5 не содержатся в контрольной работе, и здесь приводятся только основная идея этого метода.

Методами Монте-Карло называют обычно численные методы решения задач при помощи моделирования случайных величин. Эти методы используются для решения задач физики, радиотехники, химии, биологии, экономики.

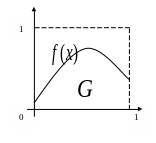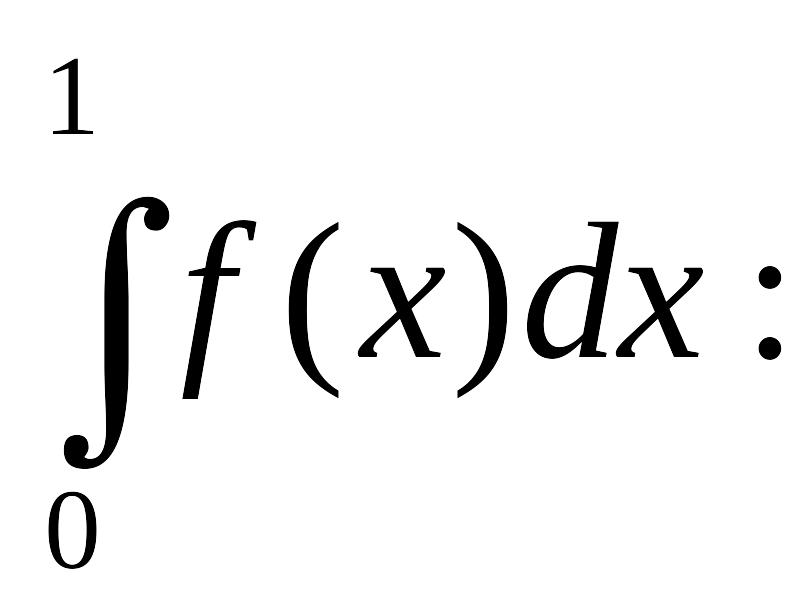
Н апример, нужно вычислить определённый интеграл: Его значение равно площади G на рисунке.

Если бросать в единичный квадрат точку, то отношение числа бросаний m, попавших в G к общему числу бросаний n даст оценку вероятности попадания в область G:

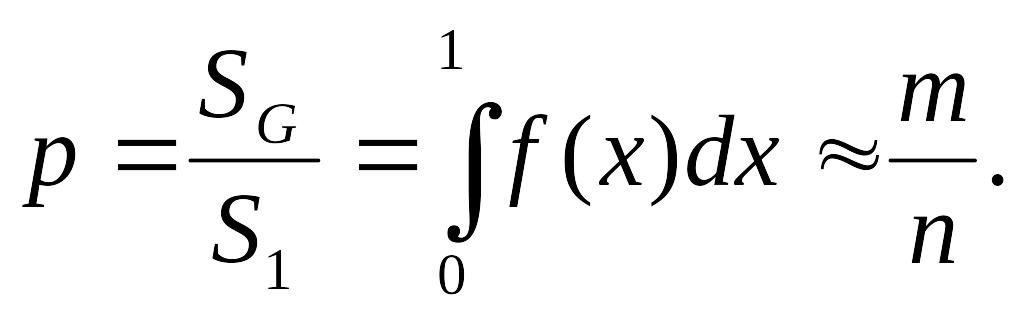А это и есть искомое значение интеграла.

Более полное изложение этой темы – в [7], c.201-249.

1.6. Численные методы алгебры

Из всех вопросов темы 1.6. Численные методы алгебры, изучается вопрос о приближённом решении уравнений.

После изучения материала опорного конспекта и письменных лекций Вам следует решить одну из задач контрольной работы согласно «Методическим указаниям к выполнению контрольной работы «Численные методы и инженерные расчёты» (с.74).

Приближённое вычисление корней уравнения

В общем случае задача отыскания точных значений корней уравнения неразрешима. Даже для алгебраических уравнений выше третьей степени нет решений в виде формул с конечным числом арифметических действий.

Сформулируем задачу следующим образом:

Дано уравнение

(1)

где - непрерывная функция в области . Корни этого уравнения – это те значения аргумента , которые обращают уравнение (1) в тождество. Найти приближённое значение корня с точностью означает указать интервал длиной не более , содержащий точное значение корня .

Решение этой задачи состоит из двух этапов:

1. Отделение корня, т.е. выделение отрезка из области непрерывности функции , содержащего только один корень уравнения (1).

2. Уточнение корня, т.е. построение итерационного процесса, позволяющего сколь угодно сузить границы выделенного интервала до значения заданной точности. Первоначальные границы его можно рассматривать как нулевое приближение искомого корня ( – с недостатком, – с избытком).

Для отделения корней уравнения (1) нужно знать те условия, которые позволяют утверждать, что, во-первых, на промежутке есть корень уравнения, а во-вторых, что он единственный на этом промежутке. Здесь следует иметь в виду следующее.

1. Если непрерывна на и имеет на концах промежутка разные знаки, то на существует нечётное количество корней. На рис.1 кривая соответствует функци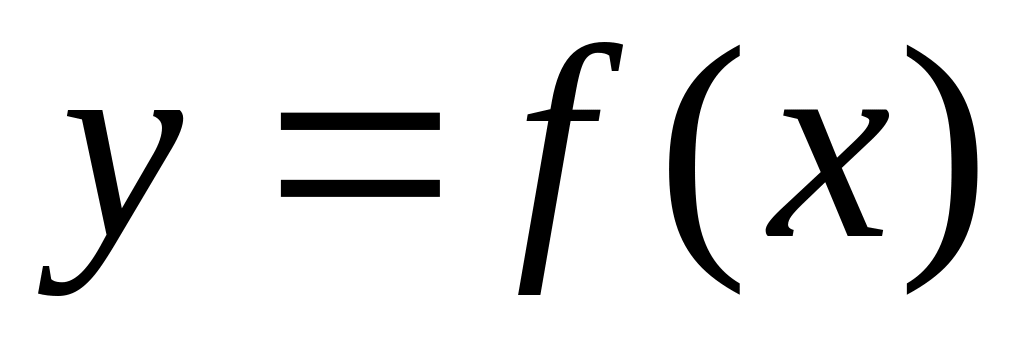и , а точки 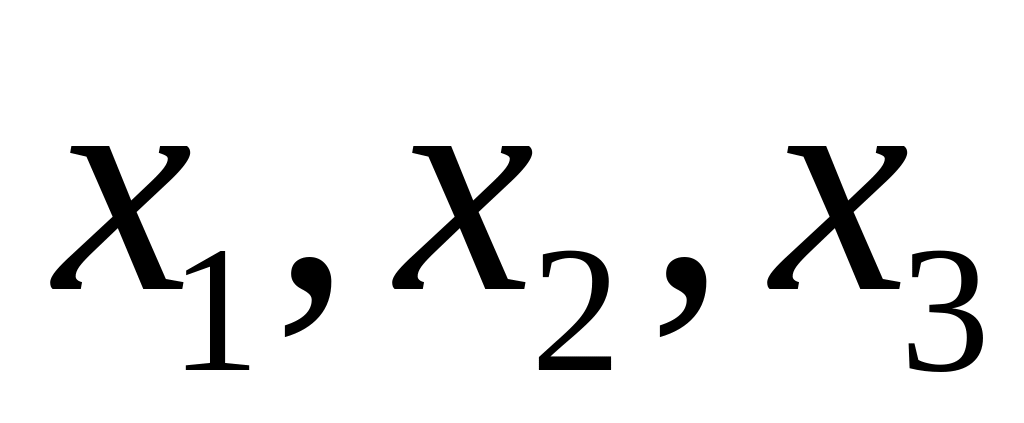– точки пересечения графика функции с осью абсцисс – корни уравнения . Т.о., разные знаки функции на концах промежутка обеспечивают наличие корня на , но не гарантируют его единственности.

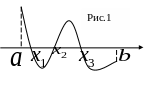
2. Если непрерывна на и имеет на концах промежутка одинаковые знаки, то, как правило, на этом промежутке число корней чётно, в том числе и 0, т.е. они могут и отсутствовать (рис.2 а, б).

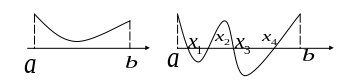
а) б)

0. Рис.2

Однако нельзя не учитывать, что корнем функции может быть не только точка пересечения графика с осью ОХ, но и точка касания с осью (рис.3 а, б, в). Заметим, что в этих случаях в точке нарушается монотонность функции .

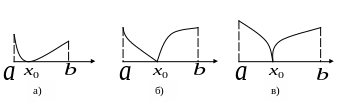
Рис.3

Таким образом, можно сформулировать следующий достаточный критерий для отделения корня: если на интервале функция непрерывна, монотонна и её значения на концах интервала имеют разные знаки, то на существует один и только один корень уравнения (1).

Из этого критерия следует, что для единственности корня на достаточно, чтобы выполнялось условие , а производная этой функции была бы знакопостоянна при любом (рис.4 а, б).

Замечание 1. Для единственности корня на при бывает достаточно и знакопостоянства второй производной (рис.4 в, г).

Рис.4

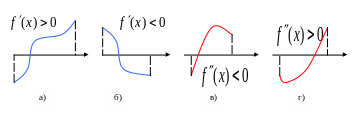
Итак, для того, чтобы отделить все вещественные корни уравнения (1), достаточно найти все интервалы монотонности , т.к. на каждом из этих интервалов может быть не более одного корня. Если на интервале монотонности , то корень есть, если , то корня нет. Интервалы монотонности соответствуют интервалам знакопостоянства .

Замечание 2. Следует рассмотреть те случаи, когда имеет одинаковые знаки на концах интервала, и, тем не менее, на нём существует корень (см. рис.3). Заметим, что в точках , соответствующих корню, производная либо не существует, либо равна нулю, либо , т.е. в этих точках достигает экстремума и, следовательно, корень является границей монотонности.

Т.о., чтобы отделить все корни уравнения (1) следует: 1) найти промежуток, где , а или , или обе производные знакопостоянны; 2) отыскать нули и точки разрыва и проверить, не являются ли они корнями уравнения (1).

Пример. Отделить все вещественные корни уравнения .

□Имеем: . Здесь непрерывна, поэтому для определения её интервалов монотонности достаточно найти нули производной : Таким образом, отделяются три промежутка монотонности и, следовательно, имеется не более трёх корней на следующих промежутках:

При этом 1.026373149, -5.026373149, следовательно, на промежутке есть единственный корень.

Чтобы отделить два оставшихся корня, вычислим , тогда на промежутке корня нет. на интервале (-2; -1) есть единственный корень. Аналогично, на интервале корня нет, а на интервале [1; 2] – также единственный корень. Графики и её первой и второй производной – рис.5 а), б), в).■

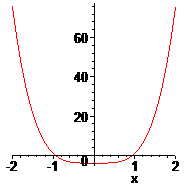
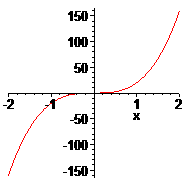
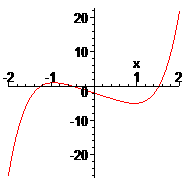
а) б) в)

Рис.5

О методах отделения корней Вы можете прочитать подробнее в [2, Раздел 4].