
Алгоритм оценки результатов измерения согласно метода наименьших квадратов
Метод
наименьших квадратов применяется для
получения оценок обработки накопленных
измерений. В том случае, если выполнено
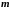 измерений координат
измерений координат
 (параметров) системы
(параметров) системы
|
(2.10) |
то поскольку компоненты вектора наблюдения
|
(2.11) |
измеряются с ошибками, то как следствие измерений получают новый вектор, то есть вектор измерений
|
(2.12) |
В выражениях (2.10) … (2.12) обозначены:
 -
n-мерный вектор
состояния системы;
-
n-мерный вектор
состояния системы;
 - квадратичная матрица
коэффициентов системы размеренности
n n;
- квадратичная матрица
коэффициентов системы размеренности
n n;
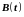 - матрица возмущений,
размеренности m
k;
- матрица возмущений,
размеренности m
k;
 - k-мерный
вектор возмущений, действующих на входе
динамической системы;
- k-мерный
вектор возмущений, действующих на входе
динамической системы;
 - матрица связи (наблюдений);
- матрица связи (наблюдений);
 - вектор измерений.
- вектор измерений.
Таким
образом, согласно вектору измерений
 и заданной матрице наблюдения
и заданной матрице наблюдения
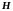 наилучшим образом оценить состояние
вектора
.
Критерием такой оценки согласно метода
наименьших квадратов служит функционал:
наилучшим образом оценить состояние
вектора
.
Критерием такой оценки согласно метода
наименьших квадратов служит функционал:
|
(2.13) |
который
минимизирует сумму квадратов ошибок
измерения
 .
.
В матричном виде критерий (2.13) имеет вид:
|
(2.14) |
или, учитывая,
что
 запишется так
запишется так
|
(2.15) |
Оценка
вектора состояния
 системы
системы
 можно получить путем решения уравнения
можно получить путем решения уравнения
|
(2.16) |
применяя которое к (2.15), получим:
|
(2.17) |
Выражение (2.17) принимает значение, равное нулю в том случае, когда согласные равны нулю:
|
(2.18) |
Из выражения
|
(2.19) |
следует
|
|
откуда
|
(2.20) |
Теперь сформируем необходимые и достаточные условия получения оптимальных оценок вектора состояния системы методом наименьших квадратов, который предусматривает:
наличие накопления наблюдений
 ;
;значение матрицы наблюдения ;
особенность матрицы
 ,
то есть
,
то есть
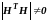 .
.
Структурная схема получения оптимальных оценок методом наименьших квадратов может быть представлена в виде рис. 2.7.
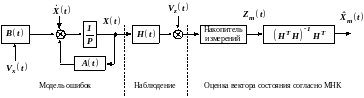
Рисунок 2.7 – Структурная схема получения оптимальных оценок
Получение
оценки
связано с накоплением наблюдений
 ,
вследствие чего новая оценка параметра
не совпадает по времени с его текущим
значением из-за необходимости времени
не накопление наблюдений. Поэтому
алгоритм МНК для оценки
используют в случае измерения одного
и того же параметра несколькими датчиками.
,
вследствие чего новая оценка параметра
не совпадает по времени с его текущим
значением из-за необходимости времени
не накопление наблюдений. Поэтому
алгоритм МНК для оценки
используют в случае измерения одного
и того же параметра несколькими датчиками.
Пример. Рассмотрим систему измерения углового положения ЛА с использованием МНК. В данной системе на основе информации от трех идентичных ИНС вычисляется угол крена ЛА. Показания первой, второй и третей ИНС соответственно равны:
|
(2.21) |
где
 - текущее значение угла крена;
- текущее значение угла крена;
 ,
,
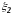 ,
,
 - ошибки ИНС (компоненты вектора
- ошибки ИНС (компоненты вектора
 ).
).
В матричной форме (2.21) имеет вид
|
(2.22) |
где
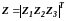 ;
;
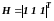 ;
;
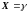 ;
;
 .
.
Итак, необходимо в соответствии с наблюдением и заданною матрицею наблюдения осуществить оценку состояния вектора .
Оценкой угла крена согласно МНК является:
, |
(2.23) |
где а)
 ;
;
б)
 ;
;
в)
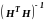
 =
= .
.
Полученные значения подставим в (2.23):
|
|
Таким образом, в данном случае значение крена определяется как среднее арифметическое показаний трех инерциальных систем.

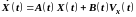 ,
,
 .
. ,
,
 .
. ,
,
 .
. и
и
 .
. ,
, .
.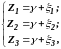
 ,
, .
.