
- •25 Поверхности уровня пот силового поля и их свойства.
- •26 Пот энергия мат точки. Примеры вычисления силовой ф-ции и пот энергии
- •28 Закон сохранения полной мех энергии системы
- •29 Сила инерции м т. Принцип даламбера для м т и мех сис-темы
- •30 Гл вектор и гл момент силы инерции. Частные случаи приведения сил инерции тв тела в различных случаях его движения
- •31 Основы аналитической механики. Классификация связей. Обобщенные координаты. Число степеней свободы. Возможные перемещения
- •32 Возможная работа силы. Идеальные связи
- •33 Обобщенные силы. Способ вычисления обобщенных сил
- •34 Принцип возможных перемещений
- •35 Условие равновесия сис-мы в обобщенных координатах. Случай потенциальных сил
- •36 Принцип даламбера-лагранжа. Общее ур-е динамики
- •37 Обобщенные силы инерции. Ур-е лагранжа 2 рода. Случай пот сил. Функция лагранжа.
- •38 Основы теории малых колебаний около положения устойчивого равновесия. Теорема лагранжа-дирихле
- •39 Кин и пот энергия системы с одной степенью свободы при малых отклонениях от устойчивого положения.
- •40 Свободные колеб мех сис-мы с одной степенью свободы
- •41 Линейное сопротивление и диссипативная функция
- •42 Свободное движение мех. Сис-мы с учетом сил сопротивления
- •43 Вынужденные колеб мех сис-мы без учета сил сопротивления
- •44 Основные понятия и допущения элементарной теории удара
- •46 Рассмотреть случай прямого удара тела о неподвижную поверхность. Коэффициент восстановления и его опытное определение.
- •47 Прямой центральный удар. Потеря кин энергии при прямом центральном ударе
- •48 Удар по вращающемуся телу. Центр удара
36 Принцип даламбера-лагранжа. Общее ур-е динамики
На
голономную систему наложены удерживающие
и идеальные связи. Применим к системе
принцип Даламбера. Такая система сил,
будет удовлетворять условию:
 ,
(1).
,
(1).
Зафиксируем
время и сообщим точкам возможные
перемещ.
.
Умножим (1) скалярно на
и просуммируем по k:
 .
в силу идеальности связей.
.
в силу идеальности связей.
 ;
;
 ,
и окончательно:
,
и окончательно:
 (общее ур-е динамики)
(общее ур-е динамики)
При любом движении механической системы с идеальными и удерживающими связями в каждый данный момент сумма возможных работ всех активных сил и сил инерции на любом возможном перемещении равна нулю.
В проекциях на декартовы оси координат:
37 Обобщенные силы инерции. Ур-е лагранжа 2 рода. Случай пот сил. Функция лагранжа.
![]() ,
(
,
(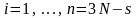 )
)
3N - число координат у N точек системы в пространстве.
s - количество связей, нахоженных на систему.
n=3N-s - число обобщ. координат определяющих положение системы (если связи голономные и удерживающие, то n - количество степеней свободы системы).
1) определить число степеней свободы механической системы и выбрать удобные обобщ. координаты;
2) вычислить Т системы в ее абсолютном движении и выразить эту энергию через обобщ. координаты и обобщ. скорости;
3) изобразить действующие на систему активные силы и силы трения, составить выражения для работы этих сил на возможном перемещ. и из этого выражения определить обобщ. силы соотв. выбранным обобщ. координатам;
4) вычислить производные, входящие в уравнения Лагранжа;
5) подставить все вычисленные величины в уравнения Лагранжа;
6) найти решения получившихся ДУ, соотв. заданным начальным условиям.
Ф-ция,
равная разности кин. и пот. энергий
механической системы, наз. ф-цией
Лагранжа, или кинетическим потенциалом:
 (
( )
=>
)
=>
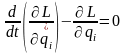
( ).
38 Основы теории малых колебаний около положения устойчивого равновесия. Теорема лагранжа-дирихле
- Механическая система может совершать малые колебания только около положения устойчивого равновесия.
- Положение системы называется положением равновесия, если в начальный момент времени система была приведена в это положение при нулевых скоростях и всё время остаётся в этом положении.
- Положение равновесия системы бывает: устойчивым, неустойчивым, безразличным.
- Под устойчивостью мех. сист. подразумевается такое ее свойство, когда все величины, определяющие ее состояние, при малых возмущениях остаются вблизи тех их значений, которые характеризуют невозмущенное состояние системы.
Л-Д: Если в некотором положении консервативной механической системы потенциальная энергия имеет строгий минимум, то это положение является положением устойчивого равновесия системы.
39 Кин и пот энергия системы с одной степенью свободы при малых отклонениях от устойчивого положения.
Система,
на которую наложены голономные, идеальные
удерживающие и стационарные связи,
состоит из N
материальных точек и движется около
положения устойчивого равновесия
системы, где
 .
.
Кинетическая
энергия системы:
![]() .
.
Радиус-вектор
каждой точки системы зависит только
от обобщенной координаты q(t):
 .
.
 ,
следовательно, кинетическая энергия
равна:
,
следовательно, кинетическая энергия
равна:
 (1).
(1).
Разложим
функцию A(q)
в окрестности положения равновесия
(![]() )
в ряд Маклорена:
)
в ряд Маклорена:
![]() (2).
(2).
Все
величины вычислены при
.
В силу малости колебаний в выражении
(1) удержим величины не выше II
порядка малости, но так как в нем уже
содержится величина II
порядка -
![]() ,
то в разложении (2) удержим только первый
постоянный член, который обозначим
«a».
Приближенное выражение кинетической
энергии:
,
то в разложении (2) удержим только первый
постоянный член, который обозначим
«a».
Приближенное выражение кинетической
энергии:
![]() .
«а» - коэфф. инерции.
.
«а» - коэфф. инерции.
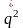 - квадрат обобщенной скорости.
- квадрат обобщенной скорости.
Система, на которую наложены голономные, идеальные удерживающие и стационарные связи, состоит из N материальных точек и движется около положения устойчивого равновесия системы, где .
Разложим потенциальную энергию в степенной ряд в окрестности положения равновесия :
![]() (1).
(1).
1-ый член в разложении (1) равен нулю, так как потенциальная энергия в положении равновесия равна нулю.
2-ой член в этом разложении равен обобщенной силе, которая в положении равновесия также равна нулю.
В силу малости колебаний потенциальная энергия должна содержать члены не выше II порядка.
Тогда:
![]() .
.
Коэфф.
при второй степени обобщенной координаты
обозначим через «с» - обобщенный коэфф.
жесткости. С учетом введенного
обозначения:
![]() .
.
